神经网络的代价函数

接下来我会再规定若干符号代表的含义：
$L$表示神经网络的总层数
$s_i$表示的是第i层的神经元数量

如果神经网络处理的是一个二元分类问题，那么他的第L层就只会有一个节点；如果处理的是一个多元分类问题，那么需要分为K类则在第L层会有K个节点

神经网络中使用的代价函数我们之前学过Logistics回归的代价函数的一般形式，其中Logistics回归的代价函数如下：（带有正则化项）
$$J(\theta )=-\frac{1}{m}\left[\sum _{i=1}^m{y}^{(i)}log{h}_{\theta }(x^{(i)})+(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))\right]+\frac{\lambda }{2m}\sum _{j=1}^n{\theta }_j^2$$

那么神经网络的代价函数为
$$J(\theta )=-\frac{1}{m}\left[\sum _{i=1}^m\sum _{k=1}^K{y}_k^{(i)}log(h_{\theta }(x^{(i)}){)}_k+(1-y_k^{(i)})log(1-(h_{\theta }(x^{(i)}){)}_k)\right]+\frac{\lambda }{2m}\sum _{l=1}^{L-1}\sum _{i=1}^{s_l}\sum _{j=1}^{s_{l+1}}({\theta }_{ji}^{(l)}{)}^2$$

我们来分析下神经网络的代价函数，在代价函数中，一般假设函数$h(x)$表示的是神经网络经过拟合后的输出值，而y是样本实际的结果，因为多分类的神经网络中，式子中的y不只是只有一种输出结果，而是有k种输出结果，因此需要计算K个输出单元的和，这就是为什么需要${\sum }_{k=1}^K$的原因。

老实说，代价函数这方面我也不太整的明白，我跟的教程并没有给出足够严谨的说明，但是好在实际使用时是直接有函数接口调用的，另外我还会找额外的书籍去补一补这一方面，等着更新吧（挖坑

反向传播算法

单个实例的反向传播

上面我们知道了神经网络的代价函数：这为我们衡量一个神经网络的假设结果是否准确提供了方法。那么如何通过调整参数$\theta$使得代价函数$J(\Theta )$最小化呢？在神经网络中，我们使用反向传播算法来实现。

这需要计算$J(\Theta )$和$\frac{\partial }{\partial {\Theta }_{ij}^{(l)}}J(\Theta )$，其中$J(\Theta )$的计算方法已经在上一节给出了，接下来的内容大部分精力都在讨论如何计算$\frac{\partial }{\partial {\Theta }_{ij}^{(l)}}J(\Theta )$

先假设只有一个训练实例$(x,y)$，试着针对这个实例进行训练，首先我们需要使用之前学的前向传播算法，获得其最终假设函数的结果。

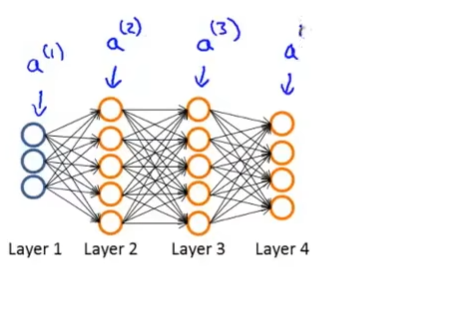
其前向传播的过程如下：
$$\begin{gathered} a^{(1)}=x \\ {z}^{(2)}={\Theta }^{(1)}{a}^{(1)} \\ {a}^{(2)}=g(z^{(2)})(add{a}_0^{(2)}) \\ {z}^{(3)}={\Theta }^{(2)}{a}^{(2)} \\ {a}^{(3)}=g(z^{(3)})(add{a}_0^{(3)}) \\ {z}^{(4)}={\Theta }^{(3)}{a}^{(3)} \\ {a}^{(4)}=h_{\Theta }(x)=g(z^{(4)}) \end{gathered}$$
注意：其中$a^{(1)}$是一个向量，其他的亦是，这是一个向量化的前向传播过程

接下来就是采用反向传播的时候了，反向传播实际上是在逐层计算神经网络的各层的假设结果和实际结果的误差。规定${\delta }_j^{(l)}$为第l层第j个节点的神经节点的激活值的误差，那么对于上述的例子有：${\delta }_j^{(4)}=a_j^{(4)}-y_j$，也就是将算法的输出值减去该样例的答案y_j。

当然，你也可以使用向量化表达，比如：${\delta }^{(4)}=a^{(4)}-y$，这个式子里的每一个元素都是一个向量，我们可以按照这种逻辑写出网络中前面几层的误差项$\delta$，如下：
$$\begin{gathered} {\delta }^{(4)}=a^{(4)}-y \\ {\delta }^{(3)}=({\Theta }^{(3)}{)}^T{\delta }^{(4)}.\ast g^{\prime }(z^{(3)}) \\ {\delta }^{(2)}=({\Theta }^{(2)}{)}^T{\delta }^{(3)}.\ast g^{\prime }(z^{(2)}) \end{gathered}$$其中$g^{\prime }(z^{(i)})=a^{(i)}.\ast (1-a^{(i)})$，这是Logistics激活函数的导数。另外误差项${\delta }_1$是不存在的，因为第一层是输入层，没有误差可言。而通过式子$$\frac{\partial }{\partial {\Theta }_{ij}^{(l)}}J(\Theta )=a_j^{(l)}{\delta }_i^{(l+1)}$$我们就可以通过式子和$a$计算出其导数项。（注意的是，现在模型尚未引入正则化的$\lambda$项，因为此时考虑正则化会比较复杂，我们后面再完成正则化工作）

多实例反向传播

现在我们试着训练一个拥有多个实例的$(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)})$，定义一个变量${\Delta }_{ij}^{(l)}=0(foralll,i,j)$这个$\Delta$表示的是误差，它的用处是用于计算导数$\frac{\partial }{\partial {\Theta }_{ij}^{(l)}}J(\Theta )$，上面单实例中，对于第l层的节点j，只会有一个实例产生误差项目$\delta$，因此$\Delta =\delta$，但是在有m个实例的多实例反向传播中，一个节点会经过m个实例的验证，因此$\Delta$等于m个单实例误差$\delta$的和。

令i从1遍历到m，依次执行以下操作：

• $a^{(1)}=x^{(i)}$
• 使用正向传播j计算每一层的激活值$a^{(l)}$
• 使用$y^{(i)}$计算${\delta }^{(L)}=a^{(L)}-y^{(i)}$，计算输出层的误差
• 并且使用该法计算各层的误差${\delta }^{(L-1)},{\delta }^{(L-2)},...,{\delta }^{(2)}$
• 接着${\Delta }_{ij}^{(l)}:={\Delta }_{ij}^{(l)}+a_j^{(l)}{\delta }_i^{(l+1)}$

完成了这些工作之后，利用上面的结果计算如下的式子
$$\begin{gathered} D_{ij}^{(l)}:=\frac{1}{m}{\Delta }_{ij}^{(l)}+\lambda {\Theta }_{ij}^{(l)}ifj\ne 0 \\ {D}_{ij}^{(l)}:=\frac{1}{m}{\Delta }_{ij}^{(l)}ifj=0 \end{gathered}$$可以看到，这里我们引入了正则化的$\lambda$项，也就是这里的作用是正则化，通过这些我们又可以计算出代价函数$J(\Theta )$的导数$\frac{\partial }{\partial {\Theta }_{ij}^{(l)}}J(\Theta )=D_{ij}^{(l)}$。这就是反向传播算法计算代价函数的过程