线性代数

高斯消元 $O(n^3))$

883. 高斯消元解线性方程组

步骤：枚举每一列：找到绝对值最大的一行，将改行换到最上面，将该行第一个数变成1，将下面所有行的第c列变成0.

#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const int maxn = 110;
const double EPS = 1e-6;
int N;
double a[maxn][maxn];
int gauss() {
	int c, r;
	for (r = 0, c = 0; c < N; c++) {
		int t = r;
		for (int i = r; i < N; i++) {
			if (fabs(a[i][c]) > fabs(a[t][c])) t = i;
		}
		if (fabs(a[t][c]) < EPS) continue;
		for (int i = c; i <= N; i++) swap(a[t][i], a[r][i]);
		for (int i = N; i >= c; i--) a[r][i] /= a[r][c];
		for (int i = r + 1; i < N; i++) {
			if (fabs(a[i][c]) > EPS) {
				for (int j = N; j >= c; j--) {
					a[i][j] -= a[r][j] * a[i][c];
				}
			}
		}
		r++;
	}
	if (r < N) {
		for (int i = r; i < N; i++) {
			if (fabs(a[i][N]) > EPS) return 2; // 无解。
		}
		return 1;  //无穷多的解
	}
	for (int i = N - 1; i >= 0; i--) {
		for (int j = i + 1; j <= N; j++) {
			a[i][N] -= a[i][j] * a[j][N];
		}
	}
	return 0;
}
int main() {
	scanf("%d", &N);
	for (int i = 0; i < N; i++) {
		for (int j = 0; j < N + 1; j++) {
			scanf("%lf", &a[i][j]);
		}
	}
	//gauss千万别忘调用啊！！！
	int t = gauss();
	if (t == 0) for (int i = 0; i < N; i++) printf("%.2f\n", a[i][N]);
	else if (t == 1) printf("Infinite group solutions\n");
	else printf("No solution\n");
	return 0;
}

884. 高斯消元解异或线性方程组

异或运算又叫不进位加法。
方法和解线性方程组一致的。

异或线性方程组示例如下：
M[1][1]x[1] ^ M[1][2]x[2] ^ … ^ M[1][n]x[n] = B[1]
M[2][1]x[1] ^ M[2][2]x[2] ^ … ^ M[2][n]x[n] = B[2]
…
M[n][1]x[1] ^ M[n][2]x[2] ^ … ^ M[n][n]x[n] = B[n]

#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
const int maxn = 110;
int a[maxn][maxn], N;
int gauss() {
	int r, c;
	for (r = c = 0; c < N; c++) {
		int t = r;
		for (int i = r; i < N; i++) {
			if (a[i][c]) {
				t = i;
				break;
			}
		}
		if (a[t][c] == 0) continue;
		for (int j = c; j <= N; j++) swap(a[t][j], a[r][j]);
        //这里放一个用bitset，求逆矩阵的部分代码。
        //小心这个地方要从第一行开始看。大雪菜那个是从 r + 1 行开始，那是因为他没有化成单位矩阵
		//但是求逆矩阵必须要化为单位阵。
        //小心这一段代码只适用于矩阵一定可逆的情况。
		//for (int i = 1; i <= N; i++) {
		//	if (a[i][c] && i != c) {
		//		a[i] ^= a[c];
		//	}
		//}
		for (int i = r + 1; i < N; i++) {
			if (a[i][c]) {
				for (int j = c; j <= N; j++) a[i][j] ^= a[r][j];
			}	
		}
		r++;
	}
	if (r < N) {
		for (int i = r; i < N; i++) {
			if (a[i][N]) return 2;
		}
		return 1;
	}
	for (int i = N - 1; i >= 0; i--) {
		for (int j = i + 1; j < N; j++) {
			a[i][N] ^= a[i][j] & a[j][N];
		}
	}
	return 0;
}
int main() {
	scanf("%d", &N);
	for (int i = 0; i < N; i++) {
		for (int j = 0; j < N + 1; j++) {
			scanf("%d", &a[i][j]);
		}
	}
	int res = gauss();
	if (res == 0) for (int i = 0; i < N; i++) printf("%d\n", a[i][N]);
	else if (res == 1) printf("Multiple sets of solutions\n");
	else printf("No solution\n");
	return 0;
}

异或矩阵求逆

我们知道 $\sim (E, A^{-1})$ . 因此，我们对输入矩阵进行高斯消元可以求逆。
下面这个输入的矩阵就是一个 $(A, E)$ ，即 $2N \times N$ 的矩阵。
底下顺便附上 $\times N$ 与 $\times 1$ 矩阵的乘法。但是为了方便，我们仍把矩阵 $B$ 写作 $\times N$ 的。
顺便说一句，高斯消元很简单，别想复杂了。

bitset<maxn * 2> a[maxn];
bitset<maxn> b;
bool Gauss_inv() {
	for (int c = 1; c <= N; c++) {
		int t = c;
		for (int i = c; i <= N; i++) {
			if (a[i][c]) {
				t = i;
				break;
			}
		}
		if (a[t][c] == 0) return false;
		swap(a[t], a[c]);
		//小心这个地方要从第一行开始看。大雪菜那个是从 r + 1 行开始，那是因为他没有化成单位矩阵
		//但是求逆矩阵必须要化为单位阵
		for (int i = 1; i <= N; i++) {
			if (a[i][c] && i != c) {
				a[i] ^= a[c];
			}
		}
	}
	return 1;
}
// A = B * C
void mul(bitset<maxn>& a, bitset<maxn> b[], bitset<maxn>& c) {
	for (int i = 1; i <= N; i++) {
		//小心这个地方是与，不是异或。矩阵乘法怎么可以写异或呢！
		a[i] = (b[i] & c).count() % 2;
	}
}

矩阵乘法

$f_n = f_1 * A^n$ ，关键就是找矩阵A是什么，然后用快速幂的思想可以快速求解。

1303. 斐波那契前 n 项和

就是求斐波那契前n项和。

#include<cstdio>
#include<cstring>
using namespace std;
const int maxn = 3;
typedef long long ll;
ll N, mod;
void mul(ll c[], ll a[], ll b[][maxn]) {
	ll tmp[maxn] = { 0 };
	for (int i = 0; i < maxn; i++) {
		for (int j = 0; j < maxn; j++) {
			tmp[i] = (tmp[i] + a[j] * b[j][i]) % mod;
		}
	}
	memcpy(c, tmp, sizeof tmp);
}
void mul(ll c[][maxn], ll a[][maxn], ll b[][maxn]) {
	ll tmp[maxn][maxn] = { 0 };
	for (int i = 0; i < maxn; i++) {
		for (int j = 0; j < maxn; j++) {
			for (int k = 0; k < maxn; k++) {
				tmp[i][j] = (tmp[i][j] + a[i][k] * b[k][j]) % mod;
			}
		}
	}
	memcpy(c, tmp, sizeof tmp);
}
int main() {
	scanf("%lld%lld", &N, &mod);
	ll f[maxn] = { 1, 1, 1 };
	ll a[maxn][maxn] = {
		{0, 1, 0},
		{1, 1, 1},
		{0, 0, 1}
	};
	N--;
	while(N){
		if (N & 1) mul(f, f, a);
		mul(a, a, a);
		N >>= 1;
	}
	printf("%lld\n", f[2]);
	return 0;
}

1304. 佳佳的斐波那契

公式自己推吧，不会的话再看看视频。
一般遇到形如 $a_1+2*a_2+3*a_3+...+n*a_n$ ，要凑成 $n*a_1+n*a_2+n*a_3+...+n*a_n$ 类似的形式。而斐波那契数列要尝试求递推公式。
其实公式推出来之后，代码长得都差不多。

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = 4;
typedef long long ll;
ll N, mod;
void mul(ll c[], ll a[], ll b[][maxn]) {
	ll tmp[maxn] = { 0 };
	for (int i = 0; i < maxn; i++) {
		for (int j = 0; j < maxn; j++) {
			tmp[i] = (tmp[i] + a[j] * b[j][i]) % mod;
		}
	}
	memcpy(c, tmp, sizeof tmp);
}
void mul(ll c[][maxn], ll a[][maxn], ll b[][maxn]) {
	ll tmp[maxn][maxn] = { 0 };
	for (int i = 0; i < maxn; i++) {
		for (int j = 0; j < maxn; j++) {
			for (int k = 0; k < maxn; k++) {
				tmp[i][j] = (tmp[i][j] + a[i][k] * b[k][j]) % mod;
			}
		}
	}
	memcpy(c, tmp, sizeof tmp);
}
int main() {
	scanf("%lld%lld", &N, &mod);
	ll f[maxn] = { 1, 1, 1, 0 };
	ll a[maxn][maxn] = {
		{0, 1, 0, 0},
		{1, 1, 1, 0},
		{0, 0, 1, 1},
		{0, 0, 0, 1}
	};
	ll n = N;
	n--;
	while (n) {
		if (n & 1) mul(f, f, a);
		mul(a, a, a);
		n >>= 1;
	}
	ll ans = (N * f[2] - f[3] + mod) % mod;
	printf("%lld\n", ans);
	return 0;
}

线性基

线性空间就是向量空间，线性空间基的数量成为该线性空间的维数。所谓的基是一组向量，就是该空间任意向量都可以由这个向量组线性表示。
线性基是向量空间的一组基，通常可以解决有关异或的一些题目。因为异或运算和加法运算很像，满足加法运算的很多性质。因此可以把整数的二进制表示看成一组向量。则线性基满足这些性质：
- 线性基的元素能相互异或得到原集合的元素的所有相互异或得到的值。
- 线性基是满足性质 1 的最小的集合（可以类比最大线性无关组）。
- 线性基没有异或和为 0 的子集（可以类比线性无关的概念）。
- 线性基中每个元素的异或方案唯一，也就是说，线性基中不同的异或组合异或出的数都是不一样的。
- 线性基中每个元素的二进制最高位互不相同。
其实，线性基还有一个很重要的性质，就是向量组的左半部分是一个单位矩阵，即每一行第一个元素是1，1这一列中对应位置的其他元素都是0.

3164. 线性基

题意：给定 n 个整数（可能重复），现在需要从中挑选任意个整数，使得选出整数的异或和最大。这个异或和的最大可能值是多少。 $1\le n \le10^5,0\le S_i \le 2^{63}-1$
把每个数写成二进制，就可以看作一个63维的向量。因此，这个题，先求出所有向量的线性基，然后把这63个向量异或起来。
怎么求线性基呢？下面的代码写的很清晰

#include<cstring>
#include<iostream>
#include<cstring>
using namespace std;
typedef long long ll;

const int maxn = 100010;
ll a[maxn];
int N;
int main() {
	scanf("%d", &N);
	for (int i = 0; i < N; i++) scanf("%lld", &a[i]);
	int k = 0;
	for (int i = 62; i >= 0; i--) {
		for (int j = k; j < N; j++) {
			if ((a[j] >> i) & 1) {
				swap(a[j], a[k]);
				break;
			}
		}
		//若没有找到了第 k 位是 1 的数，就continue;
		if (((a[k] >> i) & 1) == 0) continue;
		for (int j = 0; j < N; j++) {
			if (j != k && ((a[j] >> i) & 1)) a[j] ^= a[k];
		}
		k++;
		//最大无关组向量的个数，既不会超过向量的维数，也不会超过向量组中向量的个数。
		if (k == N) break;
	}
	//0 是(自然数，异或)这个代数结构的零元
	ll res = 0;
	for (int i = 0; i < k; i++) res ^= a[i];
	printf("%lld\n", res);
	return 0;
}

组合数学

求组合数

递推法 $O(n^2))$

885. 求组合数 I
$C_a^b = C_{a-1}^{b} + C_{a-1}^{b-1}$
类似于动态规划，预处理出所有的组合数

const int maxn = 2010, mod = 1000000007;
int c[maxn][maxn];
void pre() {
	for (int i = 0; i <= 2000; i++) {
		for (int j = 0; j <= i; j++) {
			if (j == 0) c[i][j] = 1;
			else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
		}
	}
}

公式法 $(O (n l o g n))$

886. 求组合数 II
$C_a^b=\frac{a!}{(a-b)!*b!}$
预处理出所有的阶乘。然后注意，分母要求出逆元。

ll fact[N], infact[N];
ll mod_pow(ll x, ll n) {
	ll res = 1;
	while (n) {
		if (n & 1) res = res * x % mod;
		x = x * x % mod;
		n >>= 1;
	}
	return res;
}
void pre(int n) {
	fact[0] = infact[0] = 1;
	for (int i = 1; i <= n; i++) {
		fact[i] = fact[i - 1] * i % mod;
	}
	infact[n] = mod_pow(fact[n], mod - 2);
	for(int i = n - 1; i >= 1; i--) infact[i] = infact[i + 1] * (i + 1) % mod;
}

卢卡斯定理

887. 求组合数 III

$N = 20,\ 0<=a, b <=10^{18},1<=p<=10^{5}$ .
$C_a^b\equiv C_{a\ mod\ p}^{b\ mod\ p} * C_{a/p}^{b/p} (mod\ p)$ ，其中 p 必须是质数。
不知为何，这个东西，大雪菜说不用掌握证明过程。
O2优化这样开（注意结尾不能有分号）：#pragma GCC optimize(2)

ll mod;
ll mod_pow(ll x, ll n) {
	ll res = 1;
	while (n) {
		if (n & 1) res = res * x % mod;
		x = x * x % mod;
		n >>= 1;
	}
	return res;
}
ll C(ll a, ll b) {
	ll res = 1;
	for (int i = 1, j = a; i <= b; i++, j--) {
		res = res * j % mod;
		res = res * mod_pow(i, mod - 2) % mod;
	}
	return res;
}
ll lacus(ll a, ll b) {
	if (a < mod && b < mod) return C(a, b);
	return C(a % mod, b % mod) * lacus(a / mod, b / mod) % mod;
}

阶乘分解质因数 $(O (n * l o g l o g n))$

题意：输入 $a, b$ ，求 $C_a^b$ 的值。

#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
const int maxn = 5010;
int prime[maxn], cnt, nums[maxn];
bool st[maxn];
//素数线性筛
void get_primes(int N) {
	for (int i = 2; i <= N; i++) {
		if (!st[i]) prime[cnt++] = i;
		for (int j = 0; prime[j] <= N / i; j++) {
			st[prime[j] * i] = true;
			if (i % prime[j] == 0) break;
		}
	}
}
//求 n! 中有多少个素因数p。
int get(int n, int p) {
	int res = 0;
	while (n > 0) {
		res += n / p;
		n /= p;
	}
	return res;
}
vector<int> mul(vector<int>& A, int b) {
	vector<int> C;
	int t = 0;
	for (int i = 0; i < A.size() || t; i++) {
		if (i < A.size()) t += A[i] * b;
		C.push_back(t % 10);
		t /= 10;
	}
	while (C.size() > 1 && C.back() == 0) C.pop_back();
	return C;
}
int main() {
	get_primes(5000);
	int a, b;
	scanf("%d%d", &a, &b);
	for (int i = 0; i < cnt; i++) {
		int p = prime[i];
		nums[i] = get(a, p) - get(b, p) - get(a - b, p);
	}
	vector<int> res;
	res.push_back(1);
	for (int i = 0; i < cnt; i++) {
		for (int j = 0; j < nums[i]; j++) {
			res = mul(res, prime[i]);
		}
	}
	for (int i = res.size() - 1; i >= 0; i--) printf("%d", res[i]);
	printf("\n");
	return 0;
}

扩展卢卡斯定理

求 $C_n^m$ ，其中 $1\le n, m \le 10^{18},2 \le p \le 10^6$ ，其中 $p$ 不一定是质数

第一步：把 $p$ 分解质因数，即 $\prod p_1^{k_1}p_2^{k_2}...$ ，每个质因数单独求，然后用中国剩余定理合并

第二步：求 $n! \mod p^k$

$p$ 出现了 $\lfloor\frac{n}{p}\rfloor$ 次，以及出现了 $\lfloor\frac{n}{p}\rfloor !$

$\prod\limits_{i,(i,p) = 1}^{p^k}$ 中 $i$ 一共循环了 $\lfloor \frac{n}{p^k}\rfloor$ 暴力求出 $\prod_{i,(i,p)=1}^{p^k}i$ , 然后用快速幂求它的 $\lfloor\frac{n}{p^k}\rfloor$ 次幂。

ll fac(const ll n, const ll p, const ll pk)
{
	if (!n)
		return 1;
	ll ans = 1;
	for (int i = 1; i < pk; i++)
		if (i % p)
			ans = ans * i % pk;
	ans = power(ans, n / pk, pk);
	for (int i = 1; i <= n % pk; i++)
		if (i % p)
			ans = ans * i % pk;
	return ans * fac(n / p, p, pk) % pk;
}

第三步：求 $C_{n}^{m} \mod p^k$
$C_n^m = \frac{n!}{m!(n-m)!} = \frac{\frac{n!}{p^{k_1}}}{\frac{m!}{p^{k_2}}{\frac{(n-m)!}{p^{k_3}}}}p^{k_1 - k_2 - k_3}$
这样子，分母就可以求逆元了

ll C(const ll n, const ll m, const ll p, const ll pk)
{
	if (n < m)
		return 0;
	ll f1 = fac(n, p, pk), f2 = fac(m, p, pk), f3 = fac(n - m, p, pk), cnt = 0;
	for (ll i = n; i; i /= p)
		cnt += i / p;
	for (ll i = m; i; i /= p)
		cnt -= i / p;
	for (ll i = n - m; i; i /= p)
		cnt -= i / p;
	return f1 * inv(f2, pk) % pk * inv(f3, pk) % pk * power(p, cnt, pk) % pk;
}

完整代码

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <iostream>
#include <climits>
#include <cmath>
using namespace std;
namespace zyt
{
	const int N = 1e6;
	typedef long long ll;
	ll n, m, p;
	inline ll power(ll a, ll b, const ll p = LLONG_MAX)
	{
		ll ans = 1;
		while (b)
		{
			if (b & 1)
				ans = ans * a % p;
			a = a * a % p;
			b >>= 1;
		}
		return ans;
	}
	ll fac(const ll n, const ll p, const ll pk)
	{
		if (!n)
			return 1;
		ll ans = 1;
		for (int i = 1; i < pk; i++)
			if (i % p)
				ans = ans * i % pk;
		ans = power(ans, n / pk, pk);
		for (int i = 1; i <= n % pk; i++)
			if (i % p)
				ans = ans * i % pk;
		return ans * fac(n / p, p, pk) % pk;
	}
	ll exgcd(const ll a, const ll b, ll &x, ll &y)
	{
		if (!b)
		{
			x = 1, y = 0;
			return a;
		}
		ll xx, yy, g = exgcd(b, a % b, xx, yy);
		x = yy;
		y = xx - a / b * yy;
		return g;
	}
	ll inv(const ll a, const ll p)
	{
		ll x, y;
		exgcd(a, p, x, y);
		return (x % p + p) % p;
	}
	ll C(const ll n, const ll m, const ll p, const ll pk)
	{
		if (n < m)
			return 0;
		ll f1 = fac(n, p, pk), f2 = fac(m, p, pk), f3 = fac(n - m, p, pk), cnt = 0;
		for (ll i = n; i; i /= p)
			cnt += i / p;
		for (ll i = m; i; i /= p)
			cnt -= i / p;
		for (ll i = n - m; i; i /= p)
			cnt -= i / p;
		return f1 * inv(f2, pk) % pk * inv(f3, pk) % pk * power(p, cnt, pk) % pk;
	}
	ll a[N], c[N];
	int cnt;
	inline ll CRT()
	{
		ll M = 1, ans = 0;
		for (int i = 0; i < cnt; i++)
			M *= c[i];
		for (int i = 0; i < cnt; i++)
			ans = (ans + a[i] * (M / c[i]) % M * inv(M / c[i], c[i]) % M) % M;
		return ans;
	}
	ll exlucas(const ll n, const ll m, ll p)
	{
		ll tmp = sqrt(p);
		for (int i = 2; p > 1 && i <= tmp; i++)
		{
			ll tmp = 1;
			while (p % i == 0)
				p /= i, tmp *= i;
			if (tmp > 1)
				a[cnt] = C(n, m, i, tmp), c[cnt++] = tmp;
		}
		if (p > 1)
			a[cnt] = C(n, m, p, p), c[cnt++] = p;
		return CRT();
	}
	int work()
	{
		ios::sync_with_stdio(false);
		cin >> n >> m >> p;
		cout << exlucas(n, m, p);
		return 0;
	}
}
int main()
{
	return zyt::work();
}

特殊的组合数

卡特兰数

分析的不错的一个卡特兰数总结
给定 $n$ 个 $0$ 和 $n$ 个 $1$ ，它们将按照某种顺序排成长度为 $2 n$ 的序列，求它们能排列成的所有序列中，能够满足任意前缀序列中 $0$ 的个数都不少于 $1$ 的个数的序列有多少个。
判断卡特兰数：

$h (n + 1) = h (0) * h (n) + h (1) * h (n - 1) + ... + h (n) * h (0) .$
根据定义， $0$ 的个数不少于 $1$ 的个数。

应用（补充）：
3. $n$ 对括号正确匹配数目：给定 $n$ 对括号，求括号正确配对的字符串数。 $f (n) = h (n)$
4. 矩阵链乘： $P=a_1×a_2×a_3×...×a_n$ ，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案。 $f (n) = h (n - 1)$
5. 在圆上选择 $2 n$ 个点，将这些点成对连接起来使得所得到的 $n$ 条线段不相交的方法数。 $f (2 n) = h (n)$
6. 求一个凸多边形区域划分成三角形区域的方法数： $f (n)$ 等于 $h (n - 2)$
在这里插入图片描述

从(0, 0)走到(6, 6)，总共 $C_{12}^{6}$ 种路径，而每一条不合法路径一定是经过红色的线。每一条经过红色的线的路径一定可以从某个点往后的路径，做一条关于红线轴对称的路径，到达(5, 7)点。因此不合法的路径数量是 $C_{12}^{5}$ 。
因此，递推式 $h(n)=C_{2n}^{n}-C_{2n}^{n-1}=\frac {C_{2n}^{n}}{n+1} = \frac{(2n)!}{(n+1)!*n!}$

void solve() {
	ll a = 2 * N, b = N;
	ll res = 1;
	for (ll i = b + 1; i <= a; i++) res = res * i % mod;
	for (ll i = 1; i <= b; i++) res = res * mod_pow(i, mod - 2) % mod;
	res = res * mod_pow(N + 1, mod - 2) % mod;
	printf("%lld\n", res);
}

415. 栈

这道题就是问一个序列通过一个栈可以得到多少种不同的序列。我们把入栈记为 $0$ ，入栈记为 $1$ ，那么 $0$ 的数量不少于 $1$ 的数量，而通过一串 $01$ 可以惟一得到一个序列，因此就是卡特兰数。

1645. 不同的二叉搜索树

$n$ 个节点构造出的二叉树的数量其实是一个卡特兰数。
把二叉树写成后缀表达式，刚好是 $n$ 个相同的元素和 $n - 1$ 个操作符，表达式第一个字符一定是元素，除此以外的每个操作符出现时，当前出现的元素数量一定至少是操作符数量 $+ 1$ ，这就是卡特兰数的定义。
$h (n + 1) = h (0) * h (n) + h (1) * h (n - 1) + ... + h (n) * h (0) .$ 根据这个也是可以解释为什么是卡特兰数。

斯特林数

斯特林数与其生成函数

上升幂与普通幂的相互转化

我们记上升阶乘幂 $x^{\overline{n}}=\prod_{k=0}^{n-1} (x+k)$ 。

则可以利用下面的恒等式将上升幂转化为普通幂：

$x^{\overline{n}}=\sum_{k=0}^{n} \begin{bmatrix}n\\ k\end{bmatrix} x^k$

如果将普通幂转化为上升幂，则有下面的恒等式：

$x^n=\sum_{k=0}^{n} \begin{Bmatrix}n\\ k\end{Bmatrix} (-1)^{n-k} x^{\overline{k}}$

下降幂与普通幂的相互转化

我们记下降阶乘幂 $x^{\underline{n}}=\dfrac{x!}{(x-n)!}=\prod_{k=0}^{n-1} (x-k)$ 。

则可以利用下面的恒等式将普通幂转化为下降幂：

$x^n=\sum_{k=0}^{n} \begin{Bmatrix}n\\ k\end{Bmatrix} x^{\underline{k}}$

如果将下降幂转化为普通幂，则有下面的恒等式：

$x^{\underline{n}}=\sum_{k=0}^n \begin{bmatrix}n\\ k\end{bmatrix} (-1)^{n-k} x^k$

3165. 第一类斯特林数

题意：第一类斯特林数（斯特林轮换数） $\begin{bmatrix}n\\k\end{bmatrix}$ 表示将 n 个两两不同的元素，划分为 k 个非空圆排列的方案数。现在，给定 n 和 k，请你求方案数。
圆排列定义：圆排列是排列的一种，指从 n 个不同元素中取出 m（1≤m≤n）个不同的元素排列成一个环形，既无头也无尾。两个圆排列相同当且仅当所取元素的个数相同并且元素取法一致，在环上的排列顺序一致。
第一类斯特林数的性质：
- $s_u(n,k) = s_u(n-1, k-1)+(n-1)*s_u(n-1,k)$
- $s_u(0,0)=1$
- $s_u(n, 0)=0$
- $s_u(n, n)=1$
- $s_u(n, 1) = (n-1)!$
- $\sum\limits_{k=0}^ns_u(n,k)=n!$
- $x^{n\uparrow}=x(x+1)(x+2)...(x+n-1) = \sum\limits_{k=0}^{n}s_u(n,k)x^k$ ，升阶函数就是它的生成函数

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

typedef long long ll;
const int maxn = 1010, mod = 1e9 + 7;
ll f[maxn][maxn];
int main() {
	int N, K;
	scanf("%d%d", &N, &K);
	f[0][0] = 1;
	for (int i = 1; i <= N; i++) {
		for (int j = 1; j <= i; j++) {
			f[i][j] = (f[i - 1][j - 1] + (i - 1) * f[i - 1][j]) % mod;
		}
	}
	cout << f[N][K] << endl;
	return 0;
}

3166. 第二类斯特林数

题意：第二类斯特林数（斯特林子集数） $\begin{Bmatrix}n\\k\end{Bmatrix}$ 表示将 n 个两两不同的元素，划分为 k 个非空子集的方案数。现在，给定 n 和 k，请你求方案数。
第二类斯特林数性质
- $S (n, k) = S (n - 1, k - 1) + k * S (n - 1, k)$
- $S (0, 0) = 1$
- $S (n, 0) = 0$
- $S (n, n) = 1$
- $S(n,2)=2^{n-1}-1$
- $\frac{1}{m!}\sum\limits_{k=0}^{m}(-1)^kC(m,k)(m-k)^n$
两类斯特林数的关系：

$\sum\limits_{k=0}^n\begin{bmatrix}n\\k\end{bmatrix}\begin{Bmatrix}n\\k\end{Bmatrix}=\sum\limits_{k=0}^n\begin{Bmatrix}n\\k\end{Bmatrix}\begin{bmatrix}n\\k\end{bmatrix}$

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

typedef long long ll;
const int maxn = 1010, mod = 1e9 + 7;
ll f[maxn][maxn];
int main() {
	int N, K;
	f[0][0] = 1;
	scanf("%d%d", &N, &K);
	for (int i = 1; i <= N; i++) {
		for (int j = 1; j <= i; j++) {
			f[i][j] = (f[i - 1][j - 1] + (ll)j * f[i - 1][j]) % mod;
		}
	}
	cout << f[N][K] << endl;
	return 0;
}

3020. 建筑师

题意：在数轴上建 n 个建筑，建筑的高度是1~n 的一个排列。从最左边看能看到 A 个建筑，从最右边看能看到 B 个建筑。满足上述所有条件的建筑方案有多少种？
以中间的 n 为分界线，将剩余的 n - 1 分成 A + B - 2 个部分，然后挑选 $A - 1$ 个放左边，就是 $C (A + B - 2, A - 1)$ . 那么，先按照每个块儿最高的楼把所有在一侧的块儿排序，然后将每个块儿中最高的数放在最外边，后面的块儿（被挡住）进行全排列，分块儿排列的方案数就是斯特林数。因此最后答案就是 $s_u(n-1,A+B-2)*C(A+B-2,A-1)$ .

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int maxn = 50010, maxm = 210;
typedef long long ll;
const ll mod = 1e9 + 7;

ll f[maxn][maxm], fact[maxm] = { 1 }, infact[maxm] = { 1 };

ll mod_pow(ll x, ll n) {
	ll res = 1;
	while (n) {
		if (n & 1) res = res * x % mod;
		x = x * x % mod;
		n >>= 1;
	}
	return res;
}

void init() {
	f[0][0] = 1;
	for (int i = 1; i < maxn; i++) {
		for (int j = 1; j < maxm; j++) {
			f[i][j] = (f[i - 1][j - 1] + (ll)(i - 1LL) * f[i - 1][j]) % mod;
		}
	}
	for (int i = 1; i < maxm; i++) {
		fact[i] = (ll)i * fact[i - 1] % mod;
		infact[i] = mod_pow(i, mod - 2) * infact[i - 1] % mod;
	}
}
ll C(int a, int b) {
	return fact[a] * infact[b] % mod * infact[a - b] % mod;
}
int main() {
	init();
	int T;
	scanf("%d", &T);
	while (T--) {
		int N, A, B;
		scanf("%d%d%d", &N, &A, &B);
		printf("%lld\n", f[N - 1][A + B - 2] * C(A + B - 2, A - 1) % mod);
	}
	return 0;
}

康托展开

不相邻的排列

$\sim n$ 这 $n$ 个自然数中选 $k$ 个，这 $k$ 个数中任何两个数都不相邻的组合有 $\displaystyle \binom {n-k+1}{k}$ 种。

如何理解呢？可以用插板法理解。 $n - k$ 个数字形成了 $n - k + 1$ 个空，中间放进去 $k$ 个隔板的方案数。这样子的话，从左到右标号 $\sim n$ ，就是对应的选择方案。

错位排列

圆排列

组合数的性质

容斥原理

设 U 中元素有 n 种不同的属性，而第 i 种属性称为 $P_i$ ，拥有属性 $P_i$ 的元素构成集合 $S_i$ ，那么

$\begin{split} \left|\bigcup_{i=1}^{n}S_i\right|=&\sum_{i}|S_i|-\sum_{i<j}|S_i\cap S_j|+\sum_{i<j<k}|S_i\cap S_j\cap S_k|-\cdots\\ &+(-1)^{m-1}\sum_{a_i<a_{i+1} }\left|\bigcap_{i=1}^{m}S_{a_i}\right|+\cdots+(-1)^{n-1}|S_1\cap\cdots\cap S_n| \end{split}$

即

$\left|\bigcup_{i=1}^{n}S_i\right|=\sum_{m=1}^n(-1)^{m-1}\sum_{a_i<a_{i+1} }\left|\bigcap_{i=1}^mS_{a_i}\right|$

二项式反演

设 $F (n)$ 和 $f (n)$ 是定义在非负整数集上的函数，若 $\sum\limits_{k=0}^{n}C_n^k f(n)$ ，则 $\sum\limits_{k=0}^{n} (-1)^{n-k}C_n^k F(k)$

证明：
$\begin{align} f(n)&=\sum\limits_{k=0}^{n}(-1)^{n-k}C_n^kF(k) \\ &=\sum\limits_{k=0}^n (-1)^{n-k}C_n^k (\sum\limits_{i=0}^k C_k^i f(i)) \\ &=\sum\limits_{i=0}^{n}(\sum\limits_{k=i}^{n}(-1)^{n-k}C_n^k C_k^i)f(i) \end{align}$
（上面这一步，分别算一下 $f (0), f (1), f (2)$ 出现多少次就可以得出）

其中
$$
\begin{align}
&\sum\limits_{k=i}^{n}(-1){n-k}C_n^k C_k^i \
&=\sum\limits_{k=i}^{n}(-1){n-k}C_n^i C_{n-i}^{k-i} \
&=C_n^i \sum\limits_{k=0}^{n-i}(-1){n-k-i}C_{n-i}^k \
&= C_n^i(1-1){n-i}

\end{align}
$KaTeX parse error: Can't use function '$' in math mode at position 6: 只有当 $̲n = i$ 时，上式不为0.\dots$
\sum\limits_{i=0}^{{n}(\sum\limits_{k=i}}{n}(-1)^{n-k}C_nk C_k^i)f(i) = \sum\limits_{i=0}^{n}(C_ni(1-1)^{n-i})f(i) = f(n).
$$
证毕.

有上下界约束的不定方程解的数量

求 $x_1 + x_2 + ... + x_n = m$ 的解的数量，其中 $\le x_i \le a_i$ . $1≤N≤20, 0≤M≤10^{14}, 0≤A_i≤10^{12}$
若 $\le x_i < \infty$ ，做变换 $y_i=x_i+1$ ，然后用隔板法解出为 $C_{M +N-1}^{N-1}$ 。
因此，答案就是 $C_{M + N - 1}^{N-1}-|S_1\cup S_2\cup ...\cup S_N|$ ，且 $S_i| = C_{M - N - 1 - (A_i+1)}^{N-1}$
优化：因为组合数 $C_{a}^{b}$ 中的 $b$ 每次都是 $(N - 1)!$ ，因此可以预处理出来，不然会被卡掉常数。我一开始是以为全开long long 会比较慢，后来发现大雪菜的就比我的快了20ms左右。

#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const ll mod = 1000000007, maxn = 25;
ll A[maxn], C_b, N, M;
ll mod_pow(ll x, ll n) {
	ll res = 1;
	while (n > 0) {
		if (n & 1) res = res * x % mod;
		x = x * x % mod;
		n >>= 1;
	}
	return res;
}
void pre() {
	C_b = 1;
	for (int i = 1; i < N; i++) {
		C_b = C_b * mod_pow(i, mod - 2) % mod;
	}
}


ll C(ll a, ll b) {
	if (a < b || a < 0 || b < 0) return 0;
	ll res = 1;
	for (ll i = 0; i < b; i++) {
		res = (a - i) % mod * res % mod;
	}
	return res * C_b % mod;
}
int main() {
	scanf("%lld%lld", &N, &M);
	pre();
	for (int i = 0; i < N; i++) scanf("%lld", &A[i]);
	ll ans = 0;
	for (int i = 0; i < (1 << N); i++) {
		ll a = M + N - 1, b = N - 1, sign = 1;
		for (int j = 0; j < N; j++) {
			if (i >> j & 1) {
				sign *= -1;
				a -= A[j] + 1;
			}
		}
		ans = (ans + sign * C(a, b)) % mod;
	}
	printf("%lld\n", (ans % mod + mod) % mod);
	return 0;
}

容斥原理一般化

二项式反演就是这个的一个应用

容斥原理常用于集合的计数问题，而对于两个集合的函数 $f (S), g (S)$ ，若
$f(S)=\sum_{T\subseteq S}g(T)$

那么就有

$g(S)=\sum_{T\subseteq S}(-1)^{|S|-|T|}f(T)$
接下来我们简单证明一下。我们从等式的右边开始推：

$\begin{split} &\sum_{T\subseteq S}(-1)^{|S|-|T|}f(T)\\ =&\sum_{T\subseteq S}(-1)^{|S|-|T|}\sum_{Q\subseteq T}g(Q)\\ =&\sum_{Q}g(Q)\sum_{Q\subseteq T\subseteq S}(-1)^{|S|-|T|}\\ \end{split}$

我们发现后半部分的求和与 $Q$ 无关，因此把后半部分的 $Q$ 剔除：

$=\sum_{Q}g(Q)\sum_{T\subseteq (S\setminus Q)}(-1)^{|S\setminus Q|-|T|}\\$

记关于集合 $P$ 的函数 $F(P)=\sum_{T\subseteq P}(-1)^{|P|-|T|}$ ，并化简这个函数：

$\begin{split} F(P)=&\sum_{T\subseteq P}(-1)^{|P|-|T|}\\ =&\sum_{i=0}^{|P|}C_{|P|}^i(-1)^{|P|-i}=\sum_{i=0}^{|P|}C_{|P|}^i1^i(-1)^{|P|-i}\\ =&(1-1)^{|P|}=0^{|P|} \end{split}$

因此原来的式子的值是

$\sum_{Q}g(Q)\sum_{T\subseteq (S\setminus Q)}(-1)^{|S\setminus Q|-|T|}=\sum_{Q}g(Q)F(S\setminus Q)=\sum_{Q}g(Q)\cdot 0^{|S\setminus Q|}$

分析发现，仅当 $|S\setminus Q|=0$ 时有 $0^0=1$ ，这时 $Q = S$ ，对答案的贡献就是 $g (S)$ ，其他时侯 $0^{|S\setminus Q|}=0$ ，则对答案无贡献。于是得到

$\sum_{Q}g(Q)\cdot 0^{|S\setminus Q|}=g(S)$

综上所述，得证。

容斥原理求最大公约数为 $k$ 的数对个数

设 $\le x, y \le N$ ， $f (k)$ 表示最大公约数为 $k$ 的有序数对 $(x, y)$ 的个数，求 $f (1)$ 到 $f (N)$ 的值。

欧拉函数（找 $gcd(\frac{x}{k},\frac{y}{k}) = 1$ 的数量）和莫比乌斯反演都可以写，但是不如容斥原理来得简单。

由容斥原理可以得知，先找到所有以 $k$ 为 公约数 的数对，再从中剔除所有以 $k$ 的倍数为 公约数 的数对，余下的数对就是以 $k$ 为 最大公约数 的数对。即 $f (k) =$ 以 $k$ 为 公约数 的数对个数 $-$ 以 $k$ 的倍数为 公约数 的数对个数。

进一步可发现，以 $k$ 的倍数为 公约数 的数对个数等于所有以 $k$ 的倍数为 最大公约数 的数对个数之和。于是，可以写出如下表达式：

$\lfloor (N/k) \rfloor ^2 - \sum_{i=2}^{i*k \le N} f(i*k)$

由于当 $k > N /2$ 时，我们可以直接算出 $\lfloor (N/k) \rfloor ^2$ ，因此我们可以倒过来，从 $f (N)$ 算到 $f (1)$ 就可以了。于是，我们使用容斥原理完成了本题。

for (long long k = N; k >= 1; k--) {
  f[k] = (N / k) * (N / k);
  for (long long i = k + k; i <= N; i += k) f[k] -= f[i];
}

上述方法的时间复杂度为 $\sum_{i=1}^{N} N/i)=O(N \sum_{i=1}^{N} 1/i)=O(N \log N)$ 。

DAG 计数

对 $n$ 个点带标号的有向无环图进行计数，对 $10^9+7$ 取模。 $n\leq 5\times 10^3$ 。

有标号的DAG计数（FFT） - 小蒟蒻yyb - 博客园 (cnblogs.com)

Min-max 容斥

对于满足全序关系并且其中元素满足可加减性的序列 ${x_i\}$ ，设其长度为 $n$ ，并设 $S=\{1,2,3,\cdots,n\}$ ，则有：

$\max_{i\in S}{x_i}=\sum_{T\subseteq S}{(-1)^{|T|-1}\min_{j\in T}{x_j}}$

Min-max 容斥在期望上也是成立的，即：

$E\left(\max_{i\in S}{x_i}\right)=\sum_{T\subseteq S}{(-1)^{|T|-1}E\left(\min_{j\in T}{x_j} \right)}$

$E\left(\min_{i\in S}{x_i}\right)=\sum_{T\subseteq S}{(-1)^{|T|-1}E\left(\max_{j\in T}{x_j} \right)}$

n个事件中恰有m个发生的概率

Waring公式，为方便起见，我用概率描述（所有关于离散问题的概率描述，都可以转化为组合描述，这个读者去完成）

设 $A_1,...,A_n$ 是 $n$ 个事件， $B_m$ 表示这 $n$ 个事件中正好发生 $m$ 个这个事件， $S_k:=\sum_{K\in C_n^k}P(\land_{i\in K}A_i)$ ，那么 $P(B_m)=\sum_{k=m}^n(-1)^{k-m}C_k^mS_k$ 。
注意一下，上边的 $S_k$ 本身只是一堆不一定互斥的概率之和，也就是说 $S_k$ 并不是一个概率，华林公式就是在借助容斥消除重复。
证明：
实际只要证明，对任何元事件 $x$ ，
$\sum_{M\in C_n^m}(\prod_{i\in M}[x\in A_i])(\prod_{i\notin M}(1-[x\in A_i]))=\sum_{k=m}^n(-1)^{k-m}C_k^m\sum_{K\in C_n^k}\prod_{i\in K}[x\in A_i]$

为方便起见将 $[x\in A_i]$ 记为 $a_i$ 。
于是：
$\begin{align} &\sum_{M\in C_n^m}(\prod_{i\in M}a_i)(\prod_{i\notin M}(1-a_i))\\ &=\sum_{M\in C_n^m}(\prod_{i\in M}a_i)(\sum_{T\subset N-M}(-1)^{|T|}\prod_{i\in T}a_i)\\ &=\sum_{M\in C_n^m}\sum_{T\subset N-M}(-1)^{|T|}(\prod_{i\in M}a_i)(\prod_{i\in T}a_i)\\ &=\sum_{M\in C_n^m}\sum_{M\subset K\subset N}(-1)^{|K-M|}\prod_{i\in K}a_i\\ &=\sum_{K\subset N}\sum_{M\subset K\land|M|=m}(-1)^{|K-M|}\prod_{i\in K}a_i\\ &=\sum_{K\subset N}(-1)^{|K|-m}C_{|K|}^m\prod_{i\in K}a_i\\ &=\sum_{k=m}^n(-1)^{k-m}C_k^m\sum_{K\in C_n^k}\prod_{i\in K}a_i \end{align}$

证毕.

burnside引理和polya定理

Burnside 引理

描述

设和为有限集合，表示所有从到的映射。是上的置换群，表示作用在上产生的所有等价类的集合（若中的两个映射经过中的置换作用后相等，则它们在同一等价类中），则

其中表示集合中元素的个数，且

举例

我们还是以给立方体染色为例子，则上面式子中一些符号的解释如下：
- ：立方体 6 个面的集合
- ：3 种颜色的集合
- ：直接给每个面染色，不考虑本质不同的方案的集合，共有种
- ：各种翻转操作构成的置换群
- ：本质不同的染色方案的集合
- ：对于某一种翻转操作，所有直接染色方案中，经过这种翻转后保持不变的染色方案的集合
接下来我们需要对中的所有置换进行分析，它们可以分为以下几类（方便起见，将立方体的 6 个面分别称为前、后、上、下、左、右）：
- 不动：即恒等变换，因为所有直接染色方案经过恒等变换都不变，因此它对应的
- 以两个相对面的中心连线为轴的旋转：相对面有 3 种选择，旋转的方向有两种选择，因此这类共有 6 个置换。假设选择了前、后两个面中心的连线为轴，则必须要满足上、下、左、右 4 个面的颜色一样，才能使旋转后不变，因此它对应的
- 以两个相对面的中心连线为轴的旋转：相对面有 3 种选择，旋转方向的选择对置换不再有影响，因此这类共有 3 个置换。假设选择了前、后两个面中心的连线为轴，则必须要满足上、下两个面的颜色一样，左、右两个面的颜色一样，才能使旋转后不变，因此它对应的
- 以两条相对棱的中点连线为轴的旋转：相对棱有 6 种选择，旋转方向对置换依然没有影响，因此这类共有 6 个置换。假设选择了前、上两个面的边界和下、后两个面的边界作为相对棱，则必须要满足前、上两个面的颜色一样，下、后两个面的颜色一样，左、右两个面的颜色一样，才能使旋转后不变，因此它对应的
- 以两个相对顶点的连线为轴的旋转：相对顶点有 4 种选择，旋转的方向有两种选择，因此这类共有 8 个置换。假设选择了前面的右上角和后面的左下角作为相对顶点，则必须满足前、上、右三个面的颜色一样，后、下、左三个面的颜色一样，才能使旋转后不变，因此它对应的
因此，所有本质不同的方案数为

3134. 魔法手链

题意：给定 m 种不同颜色的魔法珠子，每种颜色的珠子的个数都足够多。现在要从中挑选 n 个珠子，串成一个环形魔法手链。魔法珠子之间存在 k 对排斥关系，互相排斥的两种颜色的珠子不能相邻，否则会发生爆炸。（同一种颜色的珠子之间也可能存在排斥）请问一共可以制作出多少种不同的手链。注意，如果两个手链经旋转后能够完全重合在一起，对应位置的珠子颜色完全相同，则视为同一种手链。答案对 9973 取模。
这个题不用管对称了。因此，应为，. 那么染色方案的集合大小为d。考虑排斥的话，就是看看d个珠子形成的圆有多少种染色方案。
设，染了前 i 个珠子，最后一个珠子（即第 i + 1 个珠子）颜色是 j. 如果不排斥，就把 f(i, k) 加到 f(i + 1, j) 上面。那么，就可以用矩阵优化，用矩阵的快速幂来求。因为每次都转移都是一模一样的。
当然，对于每一个 d，我们都要这么求一遍。但是 N 比较大，不能这么求，所以枚举d，那么 0~N-1 有多少个数和N的最大公约数是 d 呢？即，那么个数就是 .

 #include<iostream>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 
 typedef long long ll;
 const ll maxn = 11, mod = 9973;
 int M;
 
 
 ll mod_pow(ll x, ll n) {
     ll res = 1;
     while (n) {
         if (n & 1) res = res * x % mod;
         x = x * x % mod;
         n >>= 1;
     }
     return res;
 }
 ll inv(ll a) {
     return mod_pow(a, mod - 2);
 }
 
 struct Matrix {
     int a[maxn][maxn];
     Matrix() {
         memset(a, 0, sizeof a);
     }
 };
 
 Matrix operator*(Matrix a, Matrix b) {
     Matrix c;
     for (int i = 1; i <= M; i++) {
         for (int j = 1; j <= M; j++) {
             for (int k = 1; k <= M; k++) {
                 c.a[i][j] = (c.a[i][j] + a.a[i][k] * b.a[k][j]) % mod;
             }
         }
     }
     return c;
 }
 
 ll qmi(Matrix a, ll n) {
     Matrix res;
     for (int i = 1; i <= M; i++) res.a[i][i] = 1;
     while (n) {
         if (n & 1) res = res * a;
         a = a * a;
         n >>= 1;
     }
     ll sum = 0;
     for (int i = 1; i <= M; i++) sum = (sum + res.a[i][i]) % mod;
     return sum;
 }
 
 ll phi(ll n) {
     ll res = n;
     for (int i = 2; i <= n / i; i++) {
         if (n % i == 0) {
             res = res / i * (i - 1);
             while (n % i == 0) n /= i;
         }
     }
     if (n > 1) res = res / n * (n - 1);
     return res % mod;
 }
 
 int main() {
     int T;
     scanf("%d", &T);
     while (T--) {
         int N, K;
         scanf("%d%d%d", &N, &M, &K);
         Matrix tr;
         for (int i = 1; i <= M; i++) {
             for (int j = 1; j <= M; j++) {
                 tr.a[i][j] = 1;
             }
         }
         for (int i = 0; i < K; i++) {
             int x, y;
             scanf("%d%d", &x, &y);
             tr.a[x][y] = tr.a[y][x] = 0;
         }
         ll res = 0;
         for (int i = 1; i <= N / i; i++) {
             if (N % i == 0) {
                 res = (res + qmi(tr, i) * phi(N / i)) % mod;
                 if (i != N / i) res = (res + qmi(tr, N / i) * phi(i)) % mod;
             }
         }
         cout << res * inv(N) % mod << endl;
     }
     return 0;
 }

Pólya 定理

描述

前置条件与 Burnside 引理相同，内容修改为

其中表示置换能拆分成的不相交的循环置换的数量。

举例

依然考虑立方体染色问题。分析刚才提到的以相对棱的中点连线为轴的旋转，如果将前、后、上、下、左、右 6 个面依次编号为 1 到 6，则该置换可以表示为（翻转后原来编号为 1 的面的位置变为了编号为 3 的面，以此类推）

因此，与刚才在 Burnside 引理中分析的结果相同。

3133. 串珠子

题意：给定 M 种不同颜色的珠子，每种颜色的珠子的个数都足够多。现在要从中挑选 N 个珠子，串成一个环形手链。请问一共可以制作出多少种不同的手链。注意，如果两个手链经旋转或翻转后能够完全重合在一起，对应位置的珠子颜色完全相同，则视为同一种手链。
对于翻转操作，有 N 个珠子，旋转 k 次（显然），那么需要旋转次才能回到最开始的状态。等于循环置换数，即 . 因此该情况答案为 .

 #include<iostream>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 
 typedef long long ll;
 int gcd(int a, int b) {
     if (b == 0) return a;
     return gcd(b, a % b);
 }
 
 ll power(ll x, ll n) {
     ll res = 1;
     while (n) {
         if (n & 1) res *= x;
         x *= x;
         n >>= 1;
     }
     return res;
 }
 
 int main() {
     int N, M;
     while (scanf("%d%d", &M, &N), N || M) {
         ll res = 0;
         for (int i = 0; i < N; i++) res += power(M, gcd(N, i));
         if (N & 1) res += (ll)N * power(M, (N + 1) / 2LL);
         else res += (ll)N / 2LL * (power(M, N / 2 + 1) + power(M, N / 2));
         cout << res / 2 / N << endl;
     }
     return 0;
 }

组合计数

递推法

1307. 牡牛和牝牛

记牡牛是1，牝牛是0。两个1之间至少要间隔k个0.
f(i)：长度为 i 且结尾是1的串，则 f(i) = f(0) + f(1) + … + f(i - k - 1). 记f(0) = 1.
然后，答案其实已经显然了，就是s(n)，而 f(i) 就是s[max(0, i - k + 1)].
然而，f(0)和s(0) 需要把初值定为1。因为 f(1) = f(0)，f(0) 定义为1是可以正确算出答案的。
dp其实就是想法很自然，边界设置很困难，因为边界设置对了才能保证不重不漏搜索到所有方案，这才是dp的实质。

正常的递推

这个是从1开始递推，比较符合正常思维。

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 100010, mod = 5000011;
int f[maxn], s[maxn], N, K;
int main() {
	scanf("%d%d", &N, &K);
	f[1] = 1, s[1] = 2;
	for (int i = 2; i <= N; i++) {
		if (i - K - 1 >= 1) f[i] = s[i - K - 1];
		else f[i] = 1;
		s[i] = (s[i - 1] + f[i]) % mod;
	}
	printf("%d\n", s[N]);
	return 0;
}

更加巧妙一些

这个是把 f(1) 和 s(1) 初始化为1

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 100010, mod = 5000011;
int f[maxn], s[maxn], N, K;
int main() {
	scanf("%d%d", &N, &K);
	f[0] = 1, s[0] = 1;
	for (int i = 1; i <= N; i++) {
		f[i] = s[max(i - K - 1, 0)];
		s[i] = (s[i - 1] + f[i]) % mod;
	}
	printf("%d\n", s[N]);
	return 0;
}

隔板法

1308. 方程的解

对于不定方程 $a_1+a_2+⋯+a_{k−1}+a_k=g(x)$ ，其中 k≥1 且 k∈N∗，x 是正整数， $g(x)=x^x\ mod\ 1000$ （即 xx 除以 1000 的余数），x,k 是给定的数。
我们要求的是这个不定方程的正整数解组数。
很简单的一个隔板问题，注意高精度的使用。

加法原理，乘法原理，组合数，排列数

1309. 车的放置

如果是一个 N * M 的棋盘，那么结果就是 $C_{n}^{k} * P_{m}^{k}$ 。不过这个题分情况讨论有点麻烦。
因此，可以上下分成两块儿，然后一行一行的往上放。就是这样：
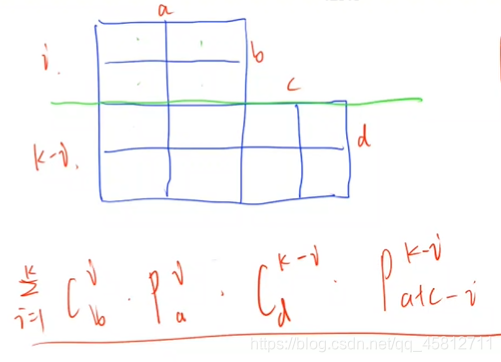
当然，如果 i > a 或 i > b，就是无解的情况，就是0。因此，我们只计算了摆的下的情况，没有计算摆不下的情况。即考虑了所有有解的情况。
这个数据范围不大，100003是个质数，而且1000!以内的数字不可能出现100003的倍数，因此我倾向于用逆元（定义法）去写。先处理出前2000的阶乘，以及前2000的阶乘的逆元。

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 2010;
typedef long long ll;
const ll mod = 100003;
ll fact[maxn] = { 1 }, infact[maxn] = { 1 };

ll mod_pow(ll x, ll n) {
	ll res = 1;
	while (n) {
		if (n & 1) res = res * x % mod;
		x = x * x % mod;
		n >>= 1;
	}
	return res;
}

void pre(int N) {
	for (ll i = 1; i <= N; i++) {
		fact[i] = i * fact[i - 1] % mod;
		infact[i] = mod_pow(i, mod - 2) * infact[i - 1] % mod;
	}
}

ll C(ll a, ll b) {
	if (b > a) return 0;
	return fact[a] * infact[b] % mod * infact[a - b] % mod;
}
ll P(ll a, ll b) {
	if (b > a) return 0;
	return fact[a] * infact[a - b] % mod;
}
int main() {
	pre(2000);
	ll a, b, c, d, k;
	scanf("%lld%lld%lld%lld%lld", &a, &b, &c, &d, &k);
	ll res = 0;
	for (int i = 0; i <= k; i++) {
		res = (res + C(b, i) * P(a, i) % mod * C(d, k - i) % mod * P(a + c - i, k - i) % mod) % mod;
	}
	printf("%lld\n", res);
	return 0;
}

1310. 数三角形

问一个方格上面可以选出多少个三角形。
乍一看没思路，其实换个问法，两点之间有多少个整数结点？这就有思路了。
大雪菜是这样划分集合的。先算出所有情况，然后减去四种可能共线的情况。斜率大于0的较难算。可以枚举小三角形的两个直角边的边长(i, j)，那么 $N * M$ 的矩形方格中总共有 $(n - i) * (m - j)$ 个。
即： $\sum (gcd(i, j) - 1) * (n-i) * (m-j).$

#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
ll N, M;
ll C_3(ll n) {
	return n * (n - 1) * (n - 2) / 6;
}
ll gcd(ll a, ll b) {
	if (b == 0) return a;
	return gcd(b, a % b);
}
int main() {
	scanf("%lld%lld", &N, &M);
	N++, M++;
	ll ans = C_3(N * M) - N * C_3(M) - M * C_3(N);
	for (int i = 1; i <= N; i++) {
		for (int j = 1; j <= M; j++) {
			ans -= 2 * (gcd(i, j) - 1) * (N - i) * (M - j);
		}
	}
	printf("%lld\n", ans);
	return 0;
}

1312. 序列统计

$0 <= a_1 <= a_2 <= ... <= a_k <= R - L$ ，则令 $x_1 = a_1, x_2 = a_2 - a_1, ... ,x_k = a_k - a_{k - 1}$ . 于是变成了 $x_1 + x_2 + ... + x_k <= R - L$ ，其中 $x_i >= 0$ 。然后令 $y_i = x_i + 1$ ，则公式变成 $y_1 + y_2 + ... +y_k <= R - L + K$ ，其中 $y_i>0$ .
总共有 $R - L + K$ 个空隙，插入K个隔板，答案就是 $C_{R-L+K}^{K}$ . 为什么K个隔板呢？其实可以这么想，每个隔板左边以上一个隔板中间夹着的小球是 $y_i$ ，这样就表示出小球没有用完的情况。由于数据范围过大，需要用卢卡斯定理。
最后还要枚举k，从1到N，令R - L = m，用上这个公式： $C_{a}^{b} = C_{a-1}^{b}+C_{a-1}^{b - 1}$ 。则答案就是 $\sum_{i=1}^{N}C_{m+i}^{i} = C_{m+1}^{1}+C_{m+2}^{2}+...+C_{m+N}^{N} = (C_{m+1}^{m+1} - 1)+C_{m+1}^{m}+C_{m+2}^{m}+...+C_{m+N}^{m} = C_{m+N+1}^{m+1} - 1 = C_{R-L+N+1}^{R-L+1} - 1$ .

#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const ll maxn = 1000010, mod = 1000003;
ll fact[maxn] = { 1 }, infact[maxn] = { 1 };
ll mod_pow(ll x, ll n) {
	ll res = 1;
	while (n) {
		if(n & 1) res = res * x % mod;
		x = x * x % mod;
		n >>= 1;
	}
	return res;
}
void pre(int N) {
	for (ll i = 1; i <= N; i++) {
		fact[i] = fact[i - 1] * i % mod;
		infact[i] = mod_pow(i, mod - 2) * infact[i - 1] % mod;
	}
}
ll C(ll a, ll b) {
	if (a < b) return 0;   //表示无解。
	return fact[a] * infact[a - b] % mod * infact[b] % mod;
}
ll lacus(ll a, ll b) {
	if (a < mod && b < mod) return C(a, b);
	return C(a % mod, b % mod) * lacus(a / mod, b / mod) % mod;
}
int main() {
	pre(maxn - 1);
	int T;
	scanf("%d", &T);
	while (T--) {
		ll N, L, R;
		scanf("%lld%lld%lld", &N, &L, &R);
		ll ans = (lacus(R - L + N + 1, R - L + 1) - 1 + mod) % mod;
		printf("%lld\n", ans);
	}
	return 0;
}

概率论

设 $X$ 取值为 $0, 1, 2, ...$ ，则
$\begin{align} &E(X) \\ =& \sum\limits_{i=0}^{\infty} i * P(X = i) \\ =& 0 * P(X = 0) + 1 * P(X = 1) + 2 * P(X = 2)+... \\ =& \sum\limits_{i=1}^{\infty} P(X \ge i) \end{align}$

概率dp

217. 绿豆蛙的归宿

有向无环图求概率期望非常好用！
给一个有向无环图，求从起点到终点的路径长度的期望。
设 $f (u)$ 是从 $u$ 到终点的路径长度的期望， $u$ 的出度为 $k$ ，连接的节点是 $v_i$ ， $X_i$ 指的就是从 $u$ 到 $v_i$ 这个事件。则 $E(\sum\limits_{i=1}^{k}\frac{1}{k}(w_i+X_i))=\sum\limits_{i=1}^{k}\frac{1}{k}(w_i+f(v_i))$

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = 100010, maxm = 200010;
int h[maxn], e[maxm], ne[maxm], idx, dout[maxn];
double w[maxm], f[maxn];
int N, M;
void add(int a, int b, int c) {
	e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
double dp(int u) {
    //小心这个地方千万不要写v!=-1，因为有浮点数误差！
	if (f[u] >= 0) return f[u];
	f[u] = 0;
	for (int i = h[u]; i != -1; i = ne[i]) {
		int v = e[i];
		f[u] += (1.0 / dout[u]) * (w[i] + dp(v));
	}
	return f[u];
}
int main() {
	scanf("%d%d", &N, &M);
	memset(h, -1, sizeof h);
	memset(f, -1, sizeof f);
	for (int i = 0; i < M; i++) {
		int a, b, c;
		scanf("%d%d%d", &a, &b, &c);
		add(a, b, c);
		dout[a]++;
	}
	printf("%.2f\n", dp(1));
	return 0;
}