本篇博客会讲解力扣“144. 二叉树的前序遍历”的解题思路，这是题目链接。

先来审题：

由于本篇博客会使用C语言来实现这道题，最简单的解法自然是使用递归。所谓前序遍历，即按照“根、左子树、右子树”的顺序来遍历，当遍历子树时，仍然按照“根、左子树、右子树”的顺序来遍历，以此类推，直到把这棵树遍历完。

由于题目要求返回一个数组，数组中存储了遍历的结果，所以我们需要使用一个下标来维护当前访问的位置。由于所有函数内部都应该是同一个遍历来表示下标，所以最好传该变量的地址。

数组需要开辟多大呢？这就需要求二叉树结点的个数了。方法很简单：仍然使用递归，总个数=左子树结点的个数+右子树结点的个数+1。

代码如下：

// 求二叉树结点的个数
int TreeSize(struct TreeNode* root)
{
    return root == NULL ? 0 : 
        TreeSize(root->left) + TreeSize(root->right) + 1;
}

void _preorderTraversal(struct TreeNode* root, int* a, int* pi)
{
    if (root == NULL)
    {
        return;
    }

    // 非空树：根，左树，右树
    a[(*pi)++] = root->val;
    _preorderTraversal(root->left, a, pi);
    _preorderTraversal(root->right, a, pi);
}

int* preorderTraversal(struct TreeNode* root, int* returnSize){
    int size = TreeSize(root);
    int* ret = (int*)malloc(sizeof(int) * size);
    *returnSize = size;

    int i = 0; // 当前访问数组的下标
    _preorderTraversal(root, ret, &i);

    return ret;
}

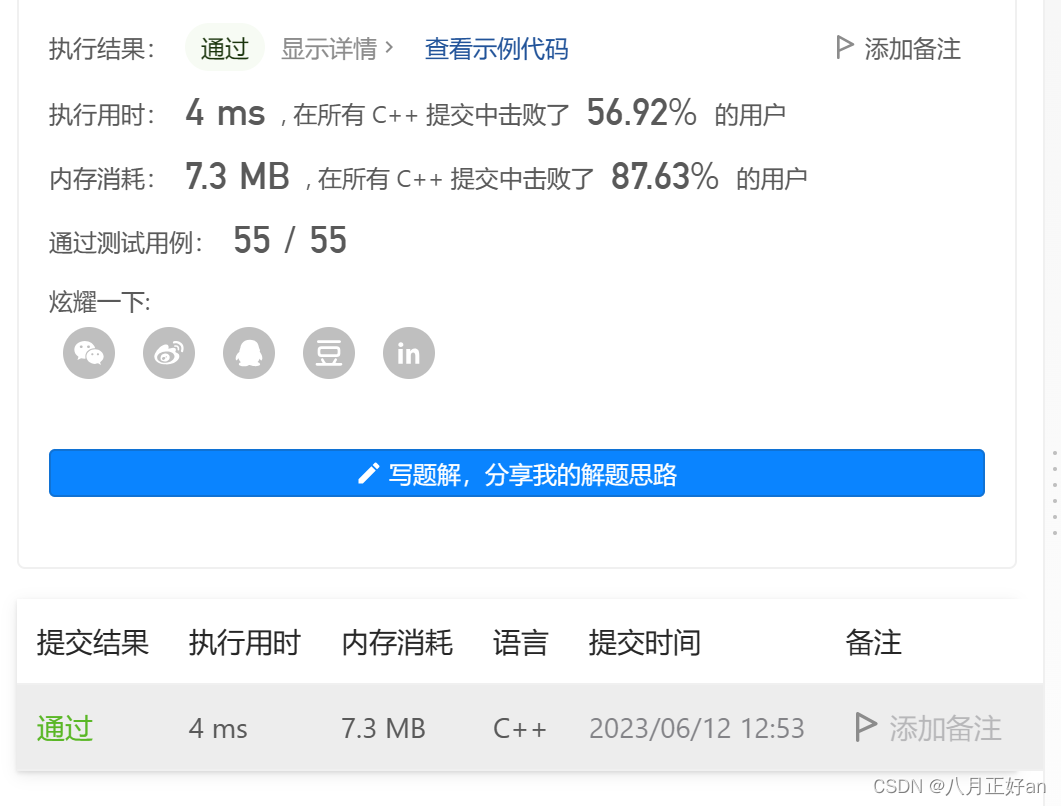
通过喽。

总结

前序遍历，即按照“根、左子树、右子树”的顺序来遍历，非常适合使用递归实现。

感谢大家的阅读！