• 注: 以下内容均由个人整理, 不保证完全准确, 如有纰漏, 欢迎交流讨论
• 参考: 杨明, 刘先忠. 矩阵论(第二版)[M]. 武汉: 华中科技大学出版社, 2005

3 矩阵的分解

3.1 常见的矩阵标准形与分解

常见标准形

• 等价标准形: $P,Q$ 可逆
  $$A_{m\times n}=P_{m\times m}\left[\begin{array}{cc}{I}_r& 0\\ 0& 0\end{array}\right]Q_{n\times n}$$
• 相似标准形: $P$ 可逆
  $$A_{n\times n}=P{J}_A{P}^{-1}$$

LU 和 LDV 分解

• LU 分解: $A\in F^{n\times n}$, 有下三角形矩阵 $L$, 上三角形矩阵 $U$, 使得 $A=LU$.
• LDV 分解: $A\in F^{n\times n}$, $L,V$ 分别是主对角线元素为 1 的下三角形和上三角形矩阵, $D$ 为对角矩阵, 使得 $A=LDV$

Th 3.1 矩阵的 $k$ 阶顺主子式: 取矩阵的前 $k$ 行、前 $k$ 列得到的行列式.
Th 3.1: $A\in F^{n\times n}$ 有唯一 LDV 分解 ⟺ $A$ 的顺主子式 $|A_k|\ne 0,k=1,2,...,n-1$, $|A_0|=1$. 其中 $D=diag(d_1,d_2,\dots ,d_n),d_k=\frac{|A_k|}{|A_{k-1}|},k=1,\dots ,n$.

LU 和 LDV 分解分解方法

LU 分解:

1. 构造增广矩阵 $(A|I)$
2. 使用第 $i$ 行乘数 $k$ 加到第 $j$ 行($i＜j$)型(不能交换两行, 也不能对一行本身乘或除一系数)行初等变换将增广矩阵 $(A|I)$ 中 $A$ 变为上三角矩阵, 此时增广矩阵为 $(U|L^{-1})$.
   $$(A|I)\stackrel{非交换两行}{⟶}(U|L^{-1})\text{(A∣I)⟶非交换两行(U∣L−1)}(A|I)\stackrel{非交换两行}{⟶}(U|L^{-1})$$
   
3. 根据增广矩阵得到的 $L^{-1}$ 求逆得 $L$.

• 最终得到 $A=LU$.

LDV 分解:

1. 进行 LU 分解得到 $L,U$
2. 从 $U$ 矩阵每行提取对角线元素的值得到矩阵 $D$
   $$U=\left[\begin{array}{cccc}{d}_1& u_{12}& \cdots & u_{1n}\\ & d_2& \cdots & u_{2n}\\ & & \ddots & ⋮\\ & & & d_n\end{array}\right]⟶D=\left[\begin{array}{cccc}{d}_1& & & \\ & d_2& & \\ & & \ddots & \\ & & & d_n\end{array}\right],V=\left[\begin{array}{cccc}1& \frac{u_{12}}{d_1}& \cdots & \frac{u_{1n}}{d_1}\\ & 1& \cdots & \frac{u_{2n}}{d_2}\\ & & \ddots & ⋮\\ & & & 1\end{array}\right]$$
   

LU 和 LDV 求解 AX=b

$$AX=b\Rightarrow \{\begin{array}{l}LY=b\\ UX=Y\end{array}$$
$$AX=b\Rightarrow \{\begin{array}{l}LZ=b\\ DY=Z\\ VX=Y\end{array}$$

满秩分解

Def 3.2: 设 $A\in F^{m\times n},rank(A)=r$, 若存在秩为 $r$ 的矩阵 $B\in F^{m\times r}$(列满秩, 瘦高矩阵), $C\in F^{r\times n}$(行满秩, 矮胖矩阵), 使得 $A=BC$, 则称此式为 $A$ 的满秩分解.

Th 3.3 任何非零矩阵 $A\in F^{m\times n}$ 都有满秩分解.

满秩分解方法

求矩阵列的极大无关组

1. 对矩阵 $A$ 进行行初等变换得到最简形矩阵, 取最简形矩阵前 $rank(A)$ 行得到矩阵 $C$.
2. 依次选择矩阵 $C$ 中每一行最左侧的 “1” 所在的列对应的 “$A$ 的列” 构成矩阵 $B$.

举例:
$$A=\left[\begin{array}{ccc}1& 1& 2\\ 0& 2& 2\\ 1& 0& 1\end{array}\right]\to \left[\begin{array}{ccc}1& 0& 1\\ 0& 1& 1\\ 0& 0& 0\end{array}\right]$$
$$C=\left[\begin{array}{ccc}1& 0& 1\\ 0& 1& 1\end{array}\right],B=\left[\begin{array}{cc}1& 1\\ 0& 2\\ 1& 0\end{array}\right]$$

可对角化矩阵的谱分解

矩阵的谱: 矩阵 $A$ 互异的特征值的集合 { λ 1 , λ 2 , . . . , λ s } \{\lambda_1,\lambda_2,...,\lambda_s\} {λ1​,λ2​,...,λs​}.

矩阵的谱分解:
$$\begin{array}{rl}A& =P({\lambda }_1\left[\begin{array}{cccc}{I}_{r_1}& & & \\ & 0& & \\ & & \ddots & \\ & & & 0\end{array}\right]+{\lambda }_2\left[\begin{array}{cccc}0& & & \\ & I_{r_2}& & \\ & & \ddots & \\ & & & 0\end{array}\right]+\cdots +{\lambda }_s\left[\begin{array}{cccc}0& & & \\ & 0& & \\ & & \ddots & \\ & & & {\lambda }_s\end{array}\right])P^{-1}\\ & =P({\lambda }_1{Q}_1+{\lambda }_2{Q}_2+\cdots +{\lambda }_s{Q}_s)P^{-1}\\ & =P(\sum _{i=1}^s{\lambda }_i{Q}_i)P^{-1}=\sum _{i=1}^s{\lambda }_{i}P{Q}_i{P}^{-1}\\ & \stackrel{def{P}_i=P{Q}_i{P}^{-1}}{========}\sum _{i=1}^s{\lambda }_i{P}_i\end{array}$$

$Q_i,P_i$ 性质:

• ${\sum }_{i=1}^s{Q}_i={\sum }_{i=1}^s{P}_i=I_n$
• $Q_i^2=Q_i,P_i^2=P_i,i=1,2,...,s$ 幂等矩阵
• $Q_i{Q}_j=0,P_i{P}_j=0,i\ne j$

Th 3.5: 矩阵可对角化 ⟺ 矩阵有谱分解 $A={\sum }_{i=1}^s{\lambda }_i{P}_i$, 其中 $P_i$ 满足上述 3 条性质.

幂等矩阵性质: $P\in F^{n\times n},P^2=P$

• $P^H,(I-P)$ 仍为幂等矩阵
• $P$ 的谱/特征值 ⊆ { 0 , 1 } \subseteq\{0,1\} ⊆{0,1}, $P$ 相似于对角矩阵
• $F^n=N(P)\oplus R(P)$, 零空间 $N(P)=V_{\lambda =0}$, 列空间 $R(P)=V_{\lambda =1}$

3.2 Schur 分解与正规矩阵

对角形矩阵

欧式空间: 实对称矩阵 $A(A^T=A)$ 相似于对角矩阵. 存在正交矩阵 $C(C{C}^T=C^{T}C=I)$:
$$C^{T}AC=C^{-1}AC=\left[\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & \ddots & \\ & & & {\lambda }_n\end{array}\right]$$

酉空间: Hermite 矩阵 $A(A^H=A)$ 相似于对角矩阵. 存在酉矩阵 $U(U{U}^H=U^{H}U=I)$:
$$U^{H}AU=U^{-1}AU=\left[\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & \ddots & \\ & & & {\lambda }_n\end{array}\right]$$

UR 和 QR 分解

Th 3.7 可逆矩阵的 UR (酉)分解:
$A\in C^{n\times n}$ 为可逆矩阵, 则存在酉矩阵(正交矩阵) $U$ 和主对角线上元素皆正的上三角矩阵 $R$, 使得 $A=UR$.

Th 3.8 列满秩矩阵(列线性无关, 瘦高矩阵)的 QR 分解:
矩阵 $A\in C^{n\times r}$ 是列满秩的矩阵, 则矩阵 $A$ 可以分解为 $A=QR$, 其中 $Q\in C^{n\times r}$ 的列向量是标准正交的向量组, $R\in C^{r\times r}$ 是主对角线上元素皆正的上三角形矩阵.

UR 和 QR 分解方法

思路: 将矩阵 $A$ 的列向量(均线性无关)视作矩阵列空间中的一组基 $A=({\alpha }_1,...,{\alpha }_r)$, 使用 Schmidt 正交化方法对其求标准正交基.
$$({\alpha }_1,{\alpha }_2,...,{\alpha }_r)=({ϵ}_1,{ϵ}_2...,{ϵ}_r)\left[\begin{array}{cccc}||{\beta }_1||& ({\alpha }_2,{ϵ}_1)& \cdots & ({\alpha }_r,{ϵ}_1)\\ & ||{\beta }_2||& \cdots & ({\alpha }_r,{ϵ}_2)\\ & & \ddots & ⋮\\ & & & ||{\beta }_r||\end{array}\right]$$

• $U$/$Q$: 标准正交基 $({ϵ}_1,{ϵ}_2...,{ϵ}_r)$
• $R$: $\left[\begin{array}{cccc}||{\beta }_1||& ({\alpha }_2,{ϵ}_1)& \cdots & ({\alpha }_r,{ϵ}_1)\\ & ||{\beta }_2||& \cdots & ({\alpha }_r,{ϵ}_2)\\ & & \ddots & ⋮\\ & & & ||{\beta }_r||\end{array}\right]$

Schur 分解

Th 3.9 Schur 分解: 对矩阵 $A\in C^{n\times n}$, 存在酉矩阵 $U$ 和上三角矩阵 $T$, 使得:
$$U^{H}AU=T=\left[\begin{array}{cccc}{\lambda }_1& \ast & \ast & \ast \\ & {\lambda }_2& \ddots & \ast \\ & & \ddots & \ast \\ & & & {\lambda }_n\end{array}\right]$$

正规矩阵 酉相似

Def’ 3.3: 方阵 $A$ 是正规矩阵 ⟺ $A^{H}A=A{A}^H$

常见的正规矩阵:

• 对角矩阵
• 实对称和反对称矩阵: $A^T=A$, $A^T=–A$
• Hermite 矩阵和反 Hermite 矩阵: $A^H=A$, $A^H=–A$
• 正交矩阵和酉矩阵: $A^{T}A=A{A}^T=I$, $A^{H}A=A{A}^H=I$

正规矩阵特性:
Th 3.10: $A\in C^{n\times n}$ 是正规矩阵 ⟺ $A$ 酉相似于对角矩阵 ("正规"是"酉相似"的不变性质).
⟺ $A$ 有 $n$ 个标准正交的特征向量.
⟺ (推论) $A$ 有 $n$ 个标准正交的特征向量构成空间 $C^n$ 的标准正交基. 即
理解: 正规矩阵关键在"酉相似于"对角矩阵. "相似"是线性变换从一组基到另一组基的坐标变换; 而"酉相似"是线性变换从一组标准正交基到另一组标准正交基的坐标变换.
⟺ $A$ 有谱分解: $A={\sum }_{i=1}^s{\lambda }_i{P}_i$. $P$ 满足: $P_i^2=P_i,P_i^H=P_i$; $P_i{P}_j=0,i\ne j$; ${\sum }_{i=1}^s{P}_i=I$. (即满足谱分解矩阵 $P_i$ 的性质外还需要满足 Hermite 性, $P_i=P{Q}_i{P}^{-1}\stackrel{正规矩阵}{⟶}{P}_i=U{Q}_i{U}^H$)

Hermite 矩阵

Hermite 矩阵: $A^H=A$

基本性质:

• Hermite 矩阵的特征值为实数, 且不同特征值对应的特征向量正交.
• $\forall A\text{ is Hermite},\exists U,U{U}^H=U^{H}U=I$: $A=Udiag({\lambda }_1,...,{\lambda }_n)U^H$ (任一 Hermite 阵 A 存在酉矩阵 U 使得 A 酉相似于对角阵)
• 半正定(正定)Hermite 阵的特征值非负(为正)
  半正定矩阵: 任意的实非零列向量 $x$ 有 $x^{T}Ax\ge 0$
  正定矩阵: 任何非零向量 $x$ 有 $x^{T}Ax>0$

Hermite 矩阵谱分解:
设 $A\in F^{n\times n}$ 是秩为 $k$ 的半正定的 Hermite 矩阵, 则 $A$ 可以分解为下列半正定矩阵的和:
$$A=v_1{v}_1^H+v_2{v}_2^H+...+v_k{v}_k^H$$
其中, { v 1 , v 2 , … , v k } \{v_1, v_2, …,v_k\} {v1​,v2​,…,vk​} 是 $F^n$ 中的正交向量组, 且秩为 1.

3.3 矩阵的奇异值分解

矩阵 $A^{H}A$ 和 $A{A}^H$

$A\in C^{m\times n}$, $A^{H}A\in C^{n\times n},A{A}^H\in C^{m\times m}$ 为 Hermite 矩阵, 从而也为正规矩阵.

Th 3.12

• $rank(A)=rank(A^{H}A)=rank(A{A}^H)$
• $A^{H}A$ 和 $A{A}^H$ 的非零特征值相等
• $A^{H}A$ 和 $A{A}^H$ 半正定.
  $r(A)=n$时, $A^{H}A\in C^{n\times n}$ 正定
  $r(A)=m$ 时, $A{A}^H\in C^{m\times m}$ 正定
  ⇒ $A^{H}A$ 和 $A{A}^H$ 的特征值是非负实数: ${\lambda }_1\ge {\lambda }_2\ge ...\ge {\lambda }_n\ge 0$

奇异值

Def’ 3.4: $A\in C^{m\times n},rank(A)=r$, 设 $A^{H}A$ 的特征值${\lambda }_1\ge {\lambda }_2\ge ...\ge {\lambda }_r>0,{\lambda }_{r+1}=...={\lambda }_n=0$, 则矩阵 $A$ 的奇异值:
$${\sigma }_i=\sqrt{{\lambda }_i},i=1,2,...,r$$
注: 此处的 ${\lambda }_i$ 是矩阵 $A^{H}A$ 的特征值, 奇异值为正(实)数

Th 3.13 奇异值性质:

• 正规矩阵 $A$ 的奇异值等于 $A$ 的(非零)特征值的模 $|{\lambda }_i|,i=1,2,...,n$
  (正规矩阵 $A^{H}A=A{A}^H=Udiag({\lambda }_n\overline{{\lambda }_n},...,{\lambda }_1\overline{{\lambda }_1})U^H$, 所以特征值 ${\sigma }_i=|{\lambda }_i|$)
• 正定的 Hermite 矩阵 $A$ 的奇异值就是 $A$ 的特征值 ${\sigma }_i={\lambda }_i$
• 若 $\exists U\in C^{m\times m},V\in C^{n\times n}$ 均为酉矩阵, $\exists B\in C^{m\times n}$: $UAV＝B$, 则称 $A$ 和 $B$ 酉等价 (等价是要求 $P,Q$ 可逆).
  酉等价的矩阵有相同的奇异值 ("奇异值"是"酉等价"的不变性质).

奇异值分解

Th 3.14 奇异值分解: 设矩阵 $A\in C^{m\times n},rank(A)=r$. ${\sigma }_1\ge {\sigma }_2\ge ...\ge {\sigma }_r>0$ 是矩阵 $A$ 的奇异值, 则存在酉矩阵 $U\in C^{m\times m},V\in C^{n\times n}$, 分块矩阵 $\Sigma =\left[\begin{array}{cc}\Delta & 0\\ 0& 0\end{array}\right]\in C^{m\times n}$, 使
$$A=U\Sigma V^H=U\left[\begin{array}{cc}\Delta & 0\\ 0& 0\end{array}\right]V^H$$
其中, $\Delta =diag({\sigma }_1,{\sigma }_2,...,{\sigma }_r)$

奇异值分解方法

目标: 求矩阵 $A_{m\times n}$ 的奇异值分解 $U\Sigma V^H$

1. 求 $A^{H}A$ 的特征值. 由非零特征值降序排序得到奇异值. $\Delta =diag({\sigma }_1,{\sigma }_2,...,{\sigma }_r)$, 进而得到矩阵 ${\Sigma }_{m\times n}$.
2. 分别求 $A^{H}A$ 特征值对应的特征向量 ${\alpha }_1,...,{\alpha }_n$, 分别将其标准化得到矩阵 $V_{n\times n}$
   $$V=(v_1,v_2,...,v_n)=(\frac{{\alpha }_1}{||{\alpha }_2||},\frac{{\alpha }_2}{||{\alpha }_1||},...,\frac{{\alpha }_n}{||{\alpha }_n||})$$
3. 利用公式 $u_i=\frac{A{v}_i}{{\sigma }_i}\text{ui=σiAvi}{u}_i=\frac{A{v}_i}{{\sigma }_i}$ 求矩阵 $U_{m\times m}=(u_1,u_2,...,u_m)$ 的每一列 $u_i$.
   当 ${\sigma }_i=0$ 时, 需要自行扩充向量 $u_i:\forall j<i,u_i\perp u_j$. 一般使用叉乘 $\times$ 计算(eg: $u_3=u_1\times u_2$).

左右奇异值向量 奇异值展开式

$A^{m\times n},rank(A)=r$
$V=(v_1,...,v_r|v_{r+1},...,v_n)=(V_1|V_2)$, $v_i$ 为右奇异向量
$U=(u_1,...,u_r|u_{r+1},...,u_m)=(U_1|U_2)$, $u_i$ 为左奇异向量

• $V_2$ 的列向量是空间 $N(A)$ 的标准正交基 ($A{V}_2=0$)
  $V_1$ 的列向量是空间 $N^{\perp }(A)$ 的标准正交基 ($V_1^H{V}_2=0$)
• $U_1$ 的列向量是 $R(A)$ 的标准正交基 ($A=U_1{\Delta }_r{V}_1^H$)
  $U_2$ 的列向量是 $R^{\perp }(A)$ 的标准正交基 ($U_1^H{U}_2=0$)

奇异值展开式:
$$A={\sigma }_1{u}_1{v}_1^H+{\sigma }_2{u}_2{v}_2^H+...+{\sigma }_r{u}_r{v}_r^H$$

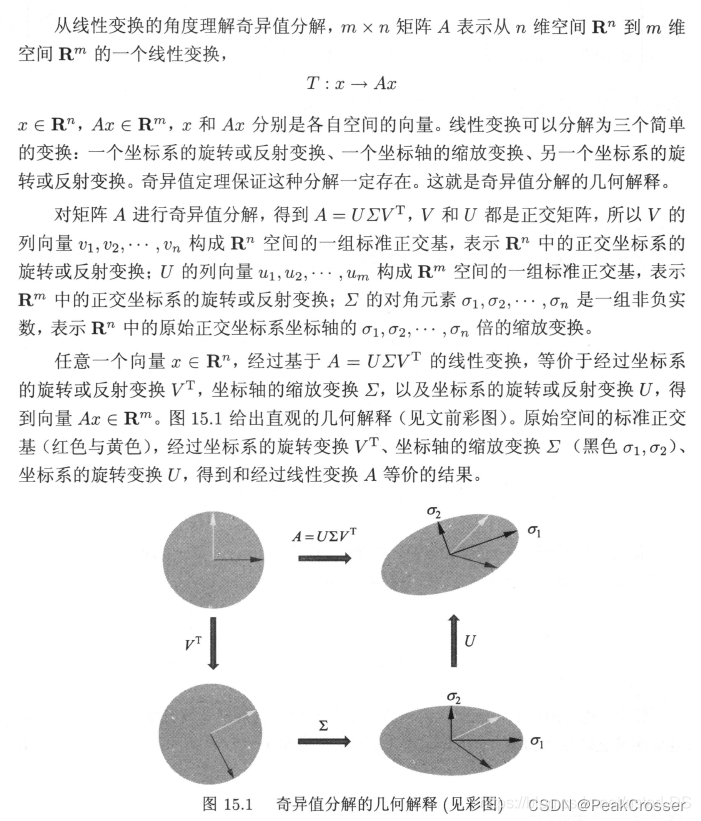
奇异值分解与线性变换

矩阵 $A\in C^{m\times n}$ 可定义线性变换 $T_A:C^n\to C^m$.
$A$ 有奇异值分解 $A=U\Sigma V^H$, 取 $U$ 和 $V$ 的列向量分别作 $C^n$ 和 $C^m$ 的标准正交基, 则线性变换 $T_A$ 对应的变换矩阵为 $\Sigma$.

$\forall \alpha =VX\in C^n$:
$$T_A(\alpha )=A\alpha =(U\Sigma V^H)VX=U(\Sigma X)=U\left[\begin{array}{c}{\sigma }_1{x}_1\\ ⋮\\ {\sigma }_r{x}_r\\ 0\\ ⋮\\ 0\end{array}\right]$$
即原像 $\alpha$ 的像在基 { u 1 , . . . , u m } \{u_1,...,u_m\} {u1​,...,um​} 的坐标为 $({\sigma }_1{x}_1,...,{\sigma }_r{x}_r,0,...,0{)}^T$.

Th 3.16 对实矩阵 $A_{m\times n}$, $R_n$ 中单位球面在线性变换 $T_A$ 下像的集合是 $R^m$:

• 球面($r=n$)
• 椭球体($r<n$)

方阵极分解

$A\in C^{n\times n},rank(A)=r$, $A$ 有极分解:
$$A=PQ=(U\Sigma U^H)(U{V}^H)$$
其中:

• $P=U\Sigma U^H\in C^{n\times n},rank(P)=r$ 是半正定 Hermite 矩阵($r=n$ 为正定矩阵), 对应在 $u_i$ 方向进行拉伸变换
• $Q=U{V}^H\in C^{n\times n}$ 是酉矩阵, 对应旋转变换