在一个多视点计算机视觉系统里，系统输入除了多个视角的图像外，一般还需要输入对应视角下相机的内外参数。其中，相机内参数决定了图像坐标系和相机三维坐标系的映射关系，而相机外参数则决定了相机三维坐标系和世界坐标系的对应关系。这两组对应关系描述了多视几何的数学基础。

先明确三个概念：1. 图像坐标：像素值的坐标x,y，最多附带一个原点平移（左上角–>图像中心）；2. 相机三维坐标系：以图像二维坐标系扩到三维，其中垂直图像外面向外的为z轴，通常以光心作为原点；3. 世界坐标系：每个视点都有自己的独立坐标系，需要投射到同一个坐标系，即世界坐标系。

我们可以通过“小孔成像”原理轻松求解出利用相机内参数求解图像坐标和相机三维坐标系的映射关系，详情可戳《【AI数学】相机成像之内参数》。本文主要讲解相机外参数的作用，即相机坐标系对世界坐标系对映射关系。

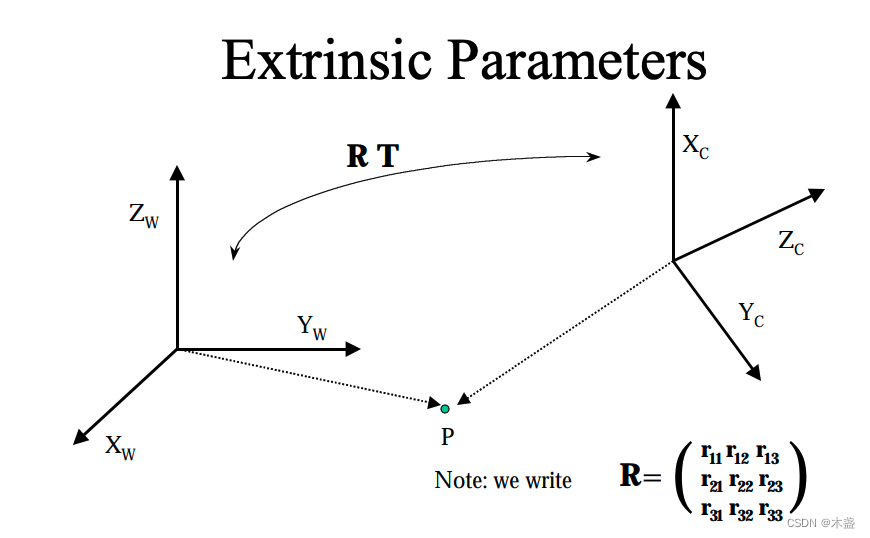
图片来自（https://ftp.cs.toronto.edu/pub/psala/VM/camera-parameters.pdf）

现在有两个坐标系$A$和$B$，空间上有一个点$P$，$P$在坐标系$A$和坐标系$B$上都有一个坐标。假如$P$在坐标系$A$中点的坐标为${\mathbf{P}}_{\mathbf{A}}=(x_A,y_A,z_A)$，在坐标系$B$中的坐标为${\mathbf{P}}_{\mathbf{B}}=(x_B,y_B,z_B)$。那么${\mathbf{P}}_{\mathbf{A}}$和${\mathbf{P}}_{\mathbf{B}}$满足什么关系呢？

所谓坐标系，无非就是一组正交基。假如坐标系$A$的单位正交基为$(\overrightarrow{a_1},\overrightarrow{a_2},\overrightarrow{a_3})$，坐标系$B$的单位正交基为$(\overrightarrow{b_1},\overrightarrow{b_2},\overrightarrow{b_3})$。这些单位正交基，都可以在同一个坐标系表示出来，只需选定一个确切的坐标系即可，我们无论选坐标系$A$、坐标系$B$或者其他坐标系都是可以的，被选定的坐标系我们通常称为“世界坐标系”。由此，我们可以发现，我们选来表示其他坐标系的单位正交基的公用坐标系就是世界坐标系。

那么，空间中一点$P$的向量可以表示为：
$$\left[\begin{array}{c}\overrightarrow{a_1},\overrightarrow{a_2},\overrightarrow{a_3}\end{array}\right]\cdot \left[\begin{array}{c}{x}_A\\ y_A\\ z_A\end{array}\right]$$
也可以表示为：
$$\left[\begin{array}{c}\overrightarrow{b_1},\overrightarrow{b_2},\overrightarrow{b_3}\end{array}\right]\cdot \left[\begin{array}{c}{x}_B\\ y_B\\ z_B\end{array}\right]$$
二者有相等（假设两个坐标系原点重合）关系。
$$\left[\begin{array}{c}\overrightarrow{a_1},\overrightarrow{a_2},\overrightarrow{a_3}\end{array}\right]\cdot \left[\begin{array}{c}{x}_A\\ y_A\\ z_A\end{array}\right]=\left[\begin{array}{c}\overrightarrow{b_1},\overrightarrow{b_2},\overrightarrow{b_3}\end{array}\right]\cdot \left[\begin{array}{c}{x}_B\\ y_B\\ z_B\end{array}\right]\text{\hspace{1em}(1)}$$
对公示(1)两边同时左乘$\left[\begin{array}{c}\overrightarrow{a_1^T}\\ \overrightarrow{a_2^T}\\ \overrightarrow{a_3^T}\end{array}\right]$，则可以将左边的系数化为单位矩阵，变换可得：
$$\left[\begin{array}{c}{x}_A\\ y_A\\ z_A\end{array}\right]=\left[\begin{array}{ccc}\overrightarrow{a_1^T}\overrightarrow{b_1}& \overrightarrow{a_1^T}\overrightarrow{b_2}& \overrightarrow{a_1^T}\overrightarrow{b_3}\\ \overrightarrow{a_2^T}\overrightarrow{b_1}& \overrightarrow{a_2^T}\overrightarrow{b_2}& \overrightarrow{a_2^T}\overrightarrow{b_3}\\ \overrightarrow{a_3^T}\overrightarrow{b_1}& \overrightarrow{a_3^T}\overrightarrow{b_2}& \overrightarrow{a_3^T}\overrightarrow{b_3}\end{array}\right]\left[\begin{array}{c}{x}_B\\ y_B\\ z_B\end{array}\right]\text{\hspace{1em}(2)}$$
我们用字母来代替公式(2)，可得：
$${\mathbf{P}}_{\mathbf{A}}=\mathbf{R}{\mathbf{P}}_{\mathbf{B}}\text{\hspace{1em}(3)}$$
公式(3)中的$\mathbf{R}$被称为旋转矩阵。旋转矩阵$\mathbf{R}$是一个行列式为1的正交矩阵，满足${\mathbf{R}}^{-1}={\mathbf{R}}^{\mathbf{T}}$。所以有
$${\mathbf{P}}_{\mathbf{B}}={\mathbf{R}}^{-1}{\mathbf{P}}_{\mathbf{A}}={\mathbf{R}}^{\mathbf{T}}{\mathbf{P}}_{\mathbf{A}}\text{\hspace{1em}(4)}$$
$\mathbf{R}$只定义了旋转，公式(3)满足两个坐标系原点相同的情况下的坐标换算。假设两个坐标系的原点并不重合，我们则需要对其进行平移。加一个三维的平移矩阵$\mathbf{T}$即可：
$${\mathbf{P}}_{\mathbf{B}}={\mathbf{R}}^{\mathbf{T}}{\mathbf{P}}_{\mathbf{A}}+\mathbf{T}\text{\hspace{1em}(5)}$$
公式(5)完成的是，两个坐标系（$A$和$B$）换算，我们称为相对位姿换算。如果把任意坐标系转换为世界坐标系，我们就称为绝对位姿换算。我们不难推出绝对位姿的换算方法，首先，我们把世界坐标系原点平移到相机坐标系：
$$\widehat{{\mathbf{P}}_{\mathbf{w}}}={\mathbf{P}}_{\mathbf{w}}-\mathbf{C}\text{\hspace{1em}(6)}$$
其中，$\mathbf{C}$为两个坐标系原点的偏移量。根据公式(3)我们可以得到：
$${\mathbf{P}}_{\mathbf{cam}}=\mathbf{R}\widehat{{\mathbf{P}}_{\mathbf{w}}}=\mathbf{R}({\mathbf{P}}_{\mathbf{w}}-\mathbf{C})=\mathbf{R}{\mathbf{P}}_{\mathbf{w}}-\mathbf{RC}=\mathbf{R}{\mathbf{P}}_{\mathbf{w}}+\mathbf{T}\text{\hspace{1em}(7)}$$
公式(7)就是本文的精髓：从世界坐标系中算出相机坐标系的坐标。其中
$$\mathbf{T}=-\mathbf{RC}\text{\hspace{1em}(8)}$$
$$\mathbf{C}=-{\mathbf{R}}^{\mathbf{T}}\mathbf{T}\text{\hspace{1em}(9)}$$
通过公式(7)，我们就可以将相机坐标系中的点换算到世界坐标系了。这里的$\mathbf{R}$和$\mathbf{T}$就是我们的相机外参数了。通常表示为一个$3\times 4$的矩阵：
$$\mathbf{E}=(\mathbf{R}\mathbf{T})\text{\hspace{1em}(10)}$$
如果需要从相机坐标系换算出世界坐标系，可依照
$${\mathbf{P}}_{\mathbf{w}}={\mathbf{R}}^{\mathbf{T}}({\mathbf{P}}_{\mathbf{cam}}-\mathbf{T})\text{\hspace{1em}(11)}$$
本文全部公式为皆为手动推理，若有疑问或指教可留言交流～