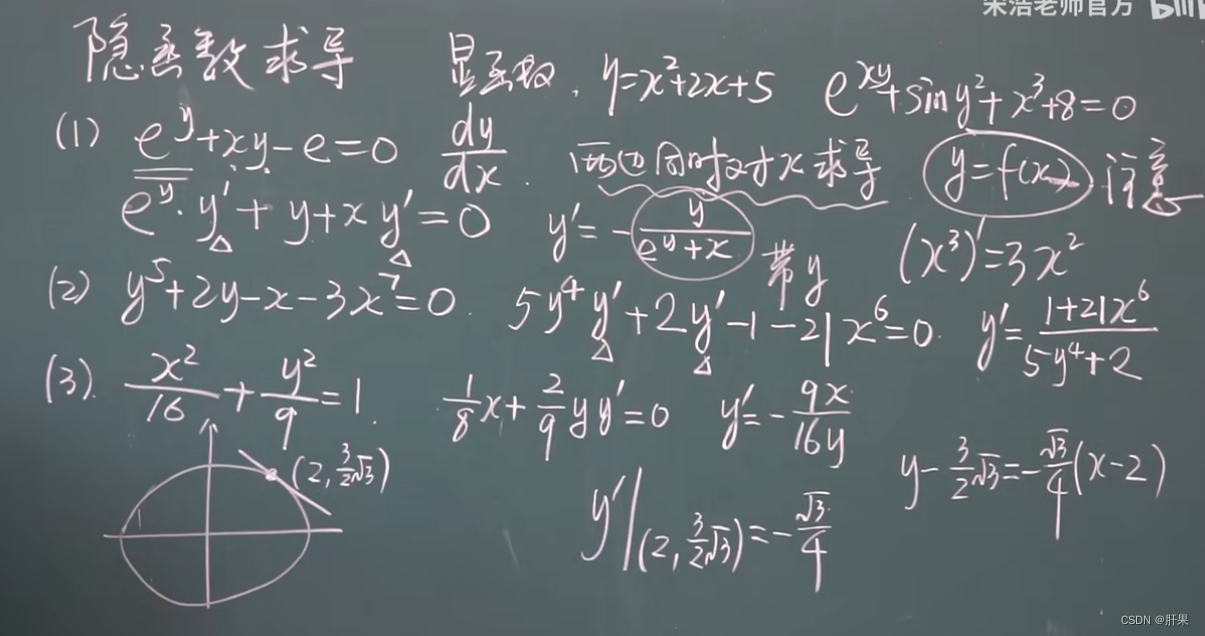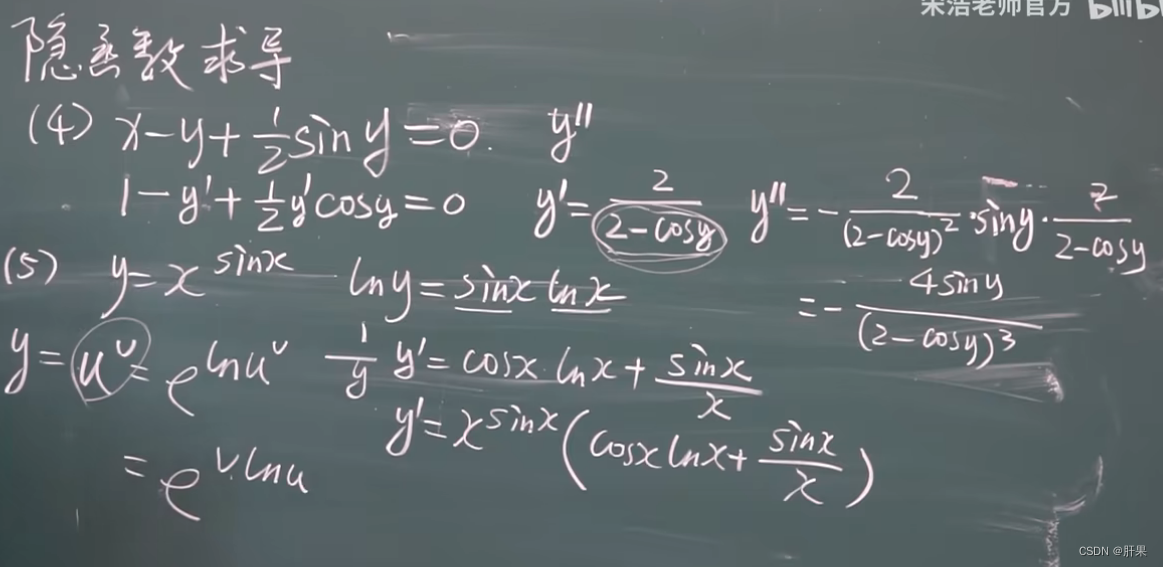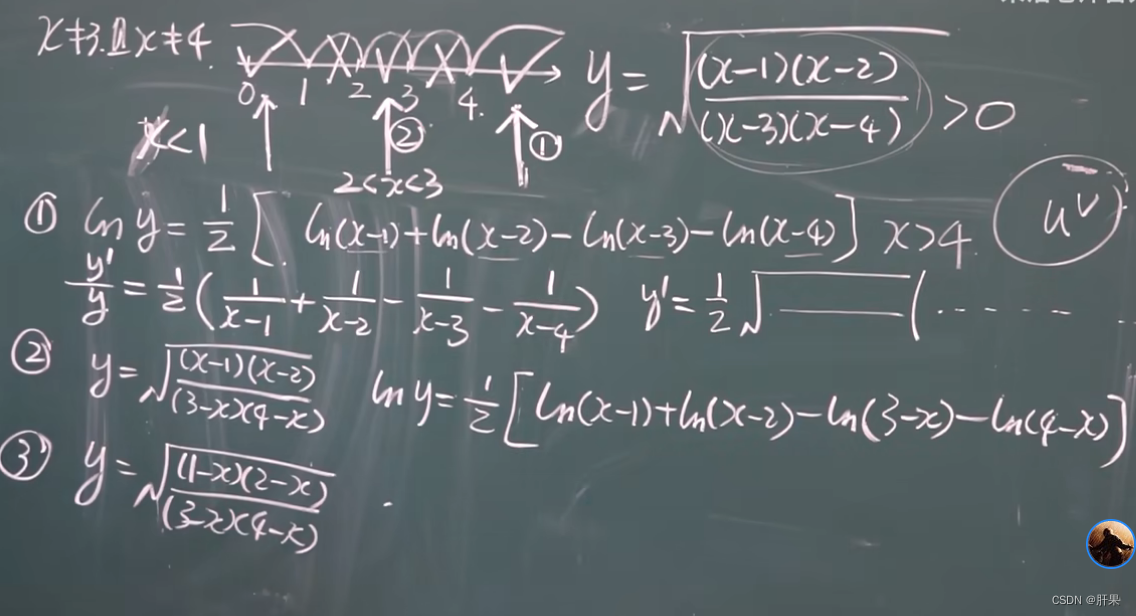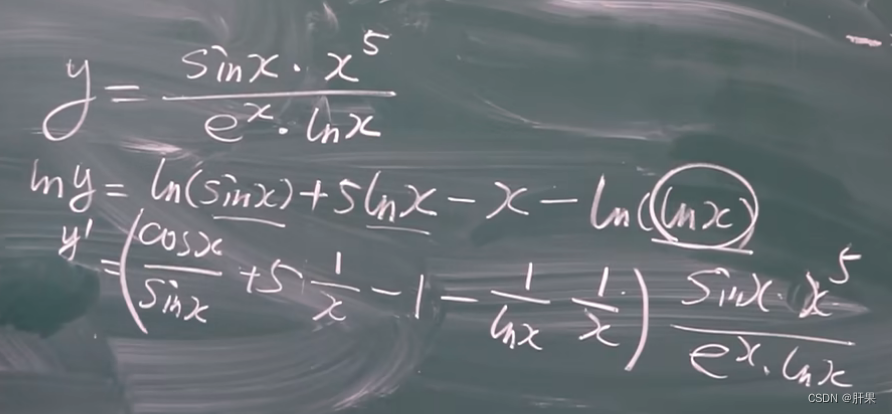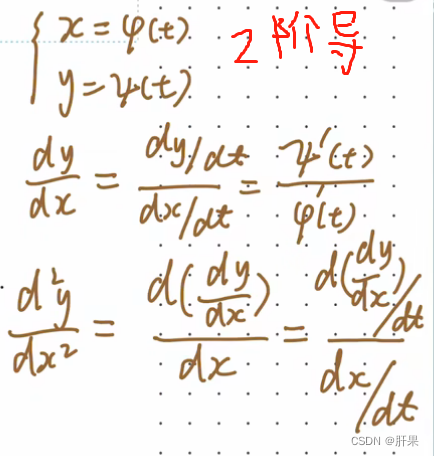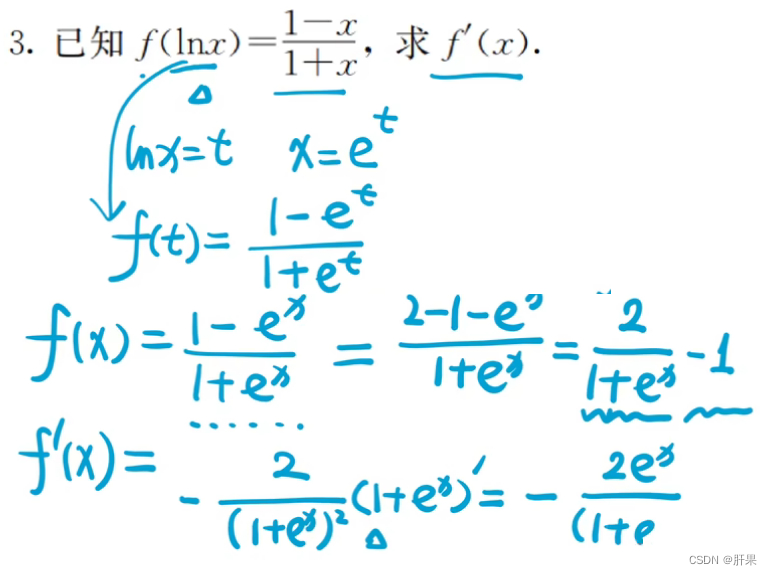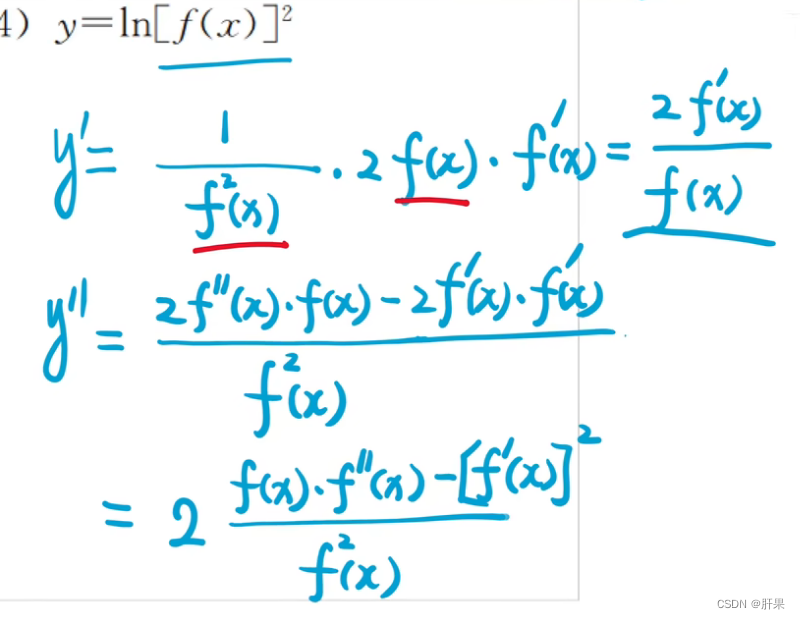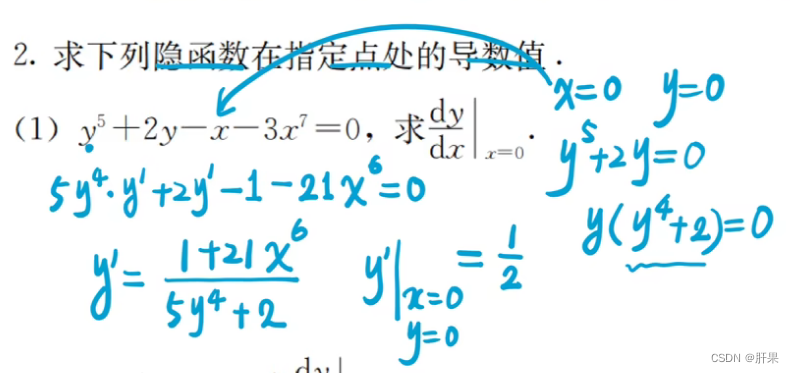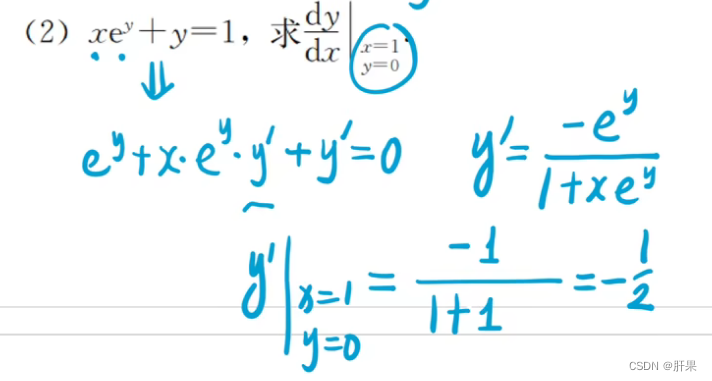导数是微积分中的一个概念,描述了函数在某一个点上的变化率。具体地说,函数 f ( x ) f(x) f(x)在 x = a x=a x=a处的导数为 f ′ ( a ) f'(a) f′(a),表示当 x x x在 a a a处发生微小的变化 Δ x \Delta x Δx时, f ( x ) f(x) f(x)对应的值 f ( a ) f(a) f(a)相应地发生的变化 Δ f \Delta f Δf与 Δ x \Delta x Δx的比值,即:
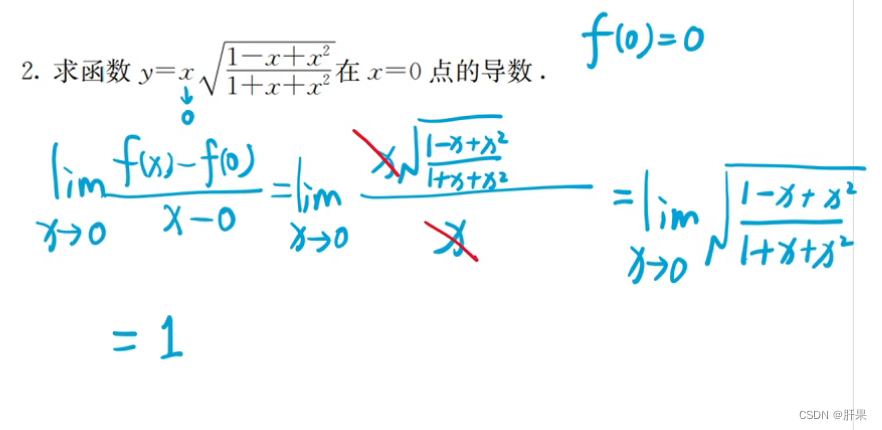
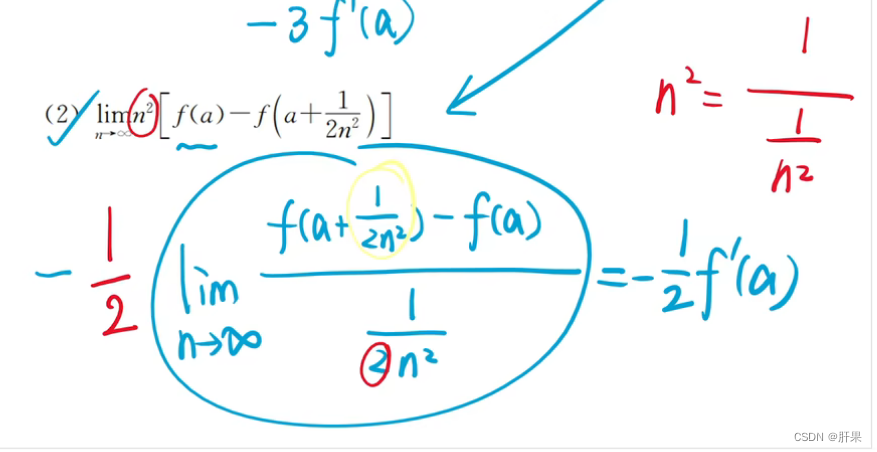
f ′ ( a ) = lim Δ x → 0 Δ f Δ x = lim Δ x → 0 f ( a + Δ x ) − f ( a ) Δ x f'(a) = \lim_{\Delta x\to 0} \frac{\Delta f}{\Delta x} = \lim_{\Delta x\to 0} \frac{f(a+\Delta x) - f(a)}{\Delta x} f′(a)=Δx→0limΔxΔf=Δx→0limΔxf(a+Δx)−f(a)
导数可以帮助我们判断函数在某一个点上是递增还是递减,并且可以用来求极值和确定函数的曲线形状等。具体地说,如果导数
f
′
(
x
)
f'(x)
f′(x)在
x
=
a
x=a
x=a处为正,则说明函数在该点附近是递增的;如果导数
f
′
(
x
)
f'(x)
f′(x)在
x
=
a
x=a
x=a处为负,则说明函数在该点附近是递减的;如果导数
f
′
(
x
)
f'(x)
f′(x)在
x
=
a
x=a
x=a处为零,可能是函数的局部极值点或拐点。

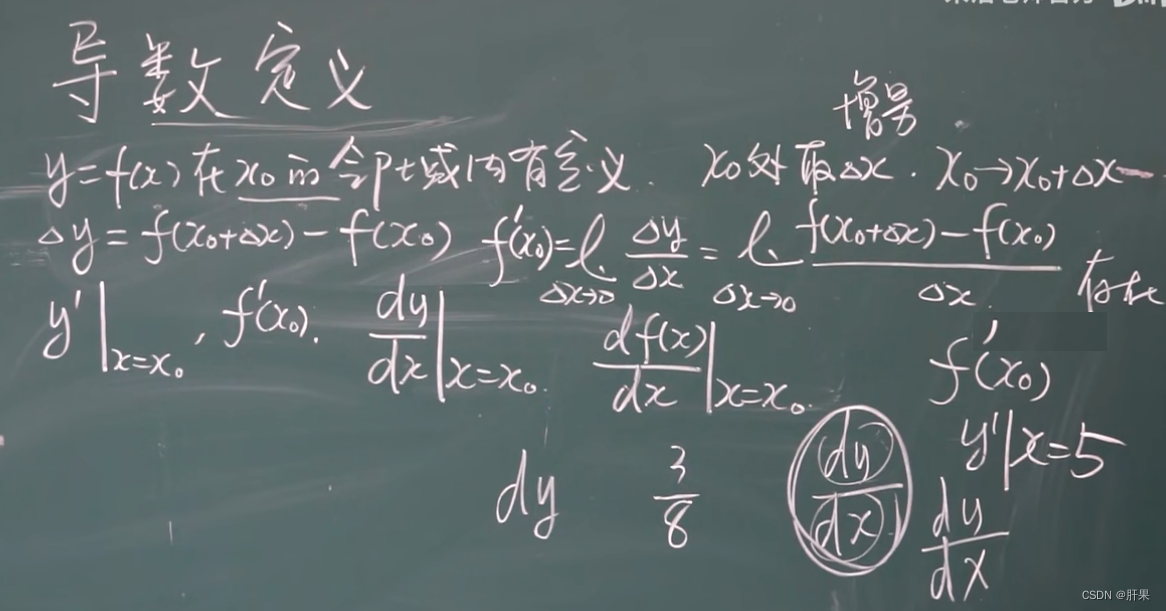
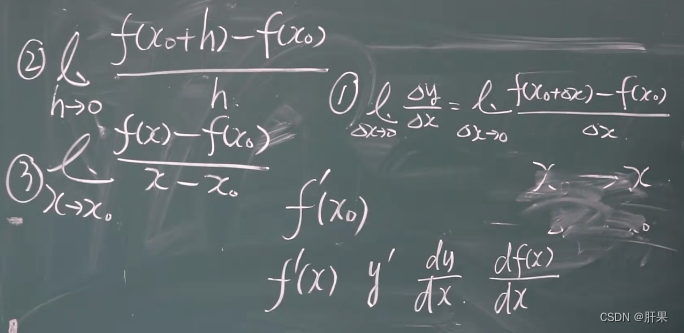
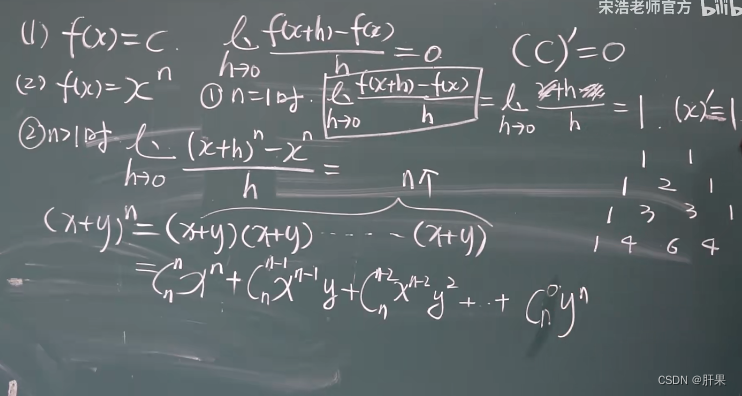
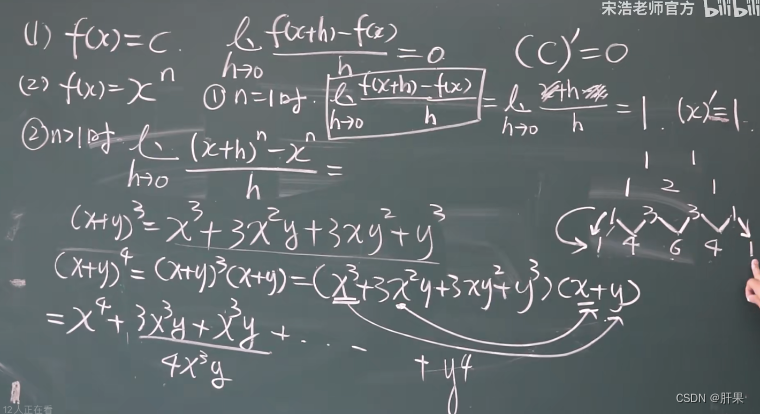
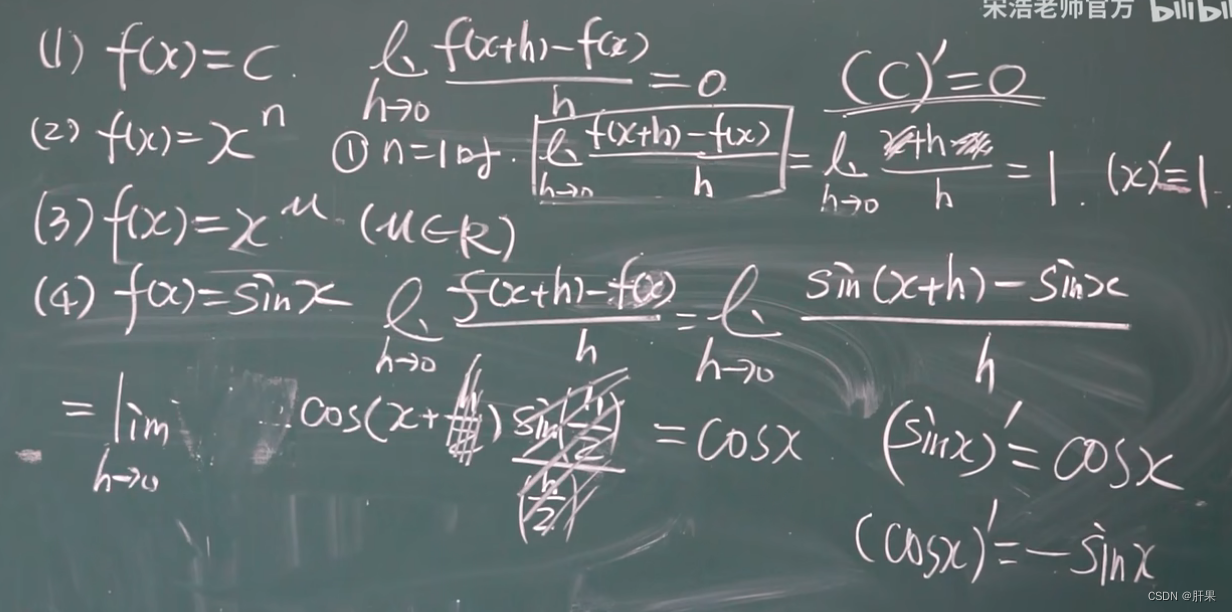
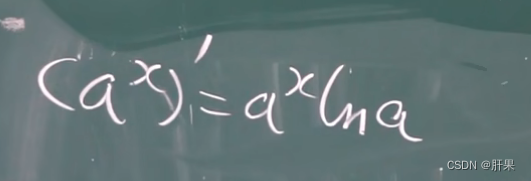
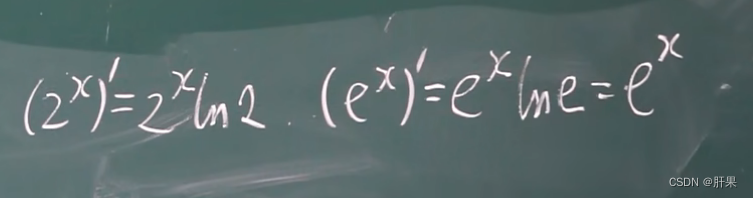
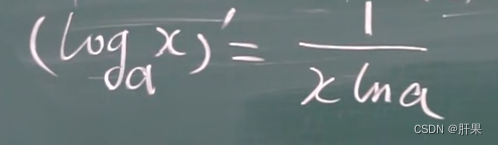
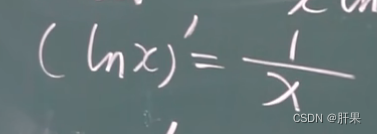
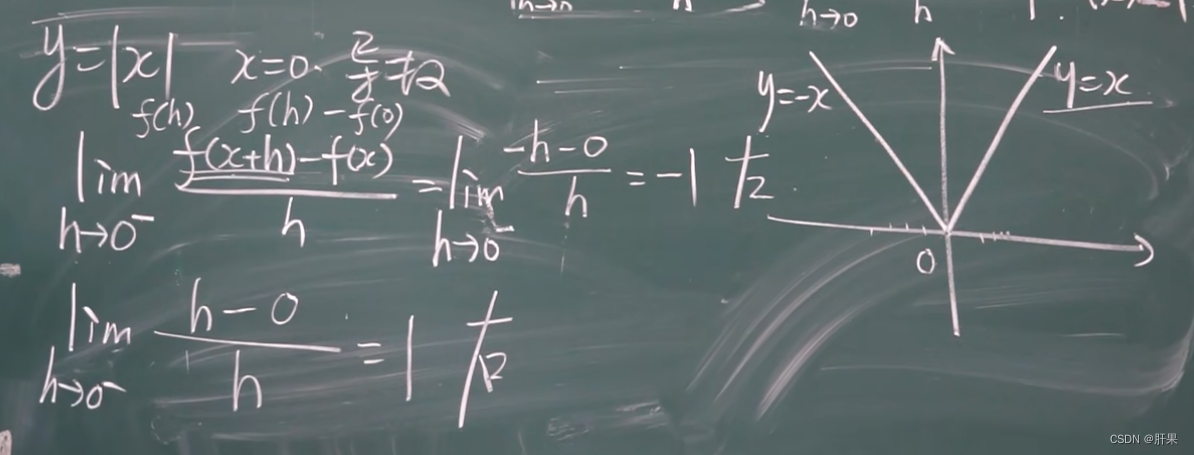
单侧导数
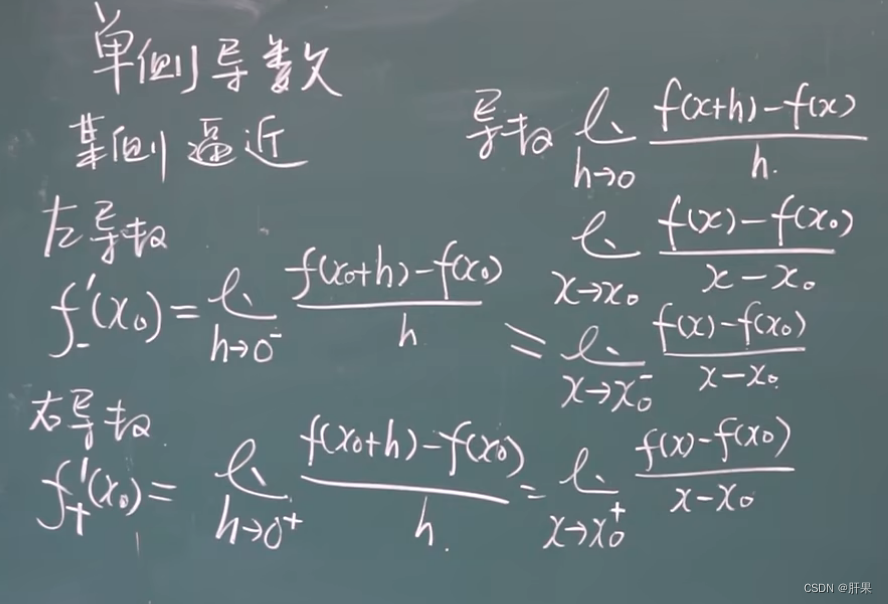

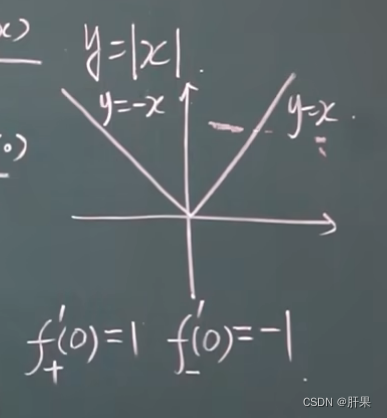

导数的几何含义
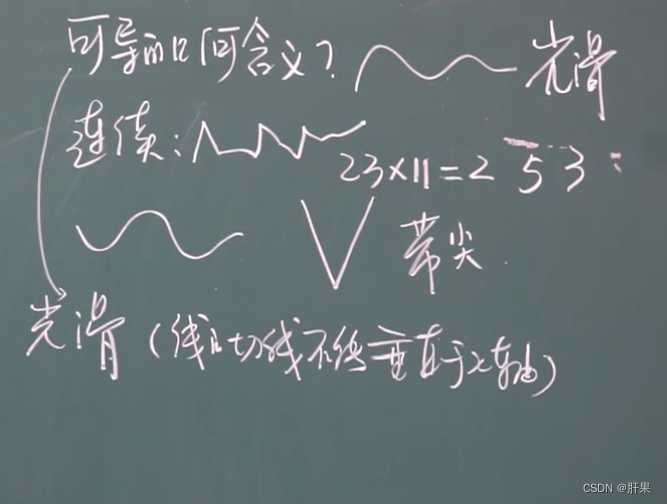
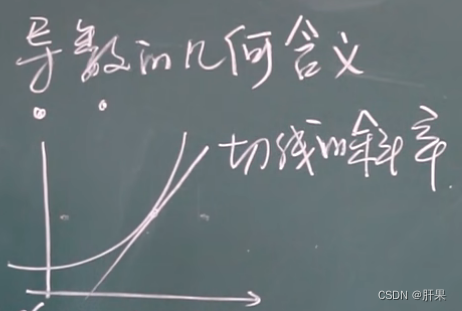
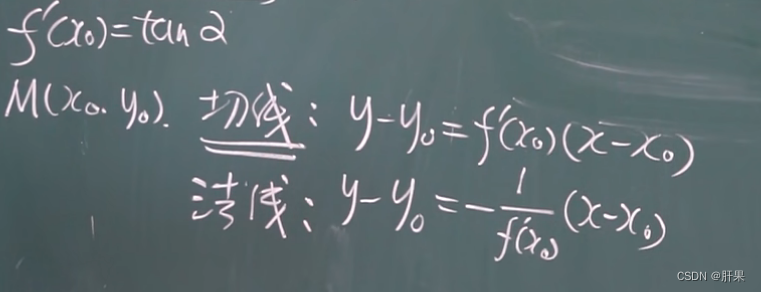
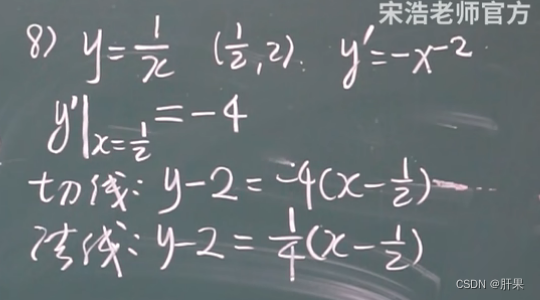
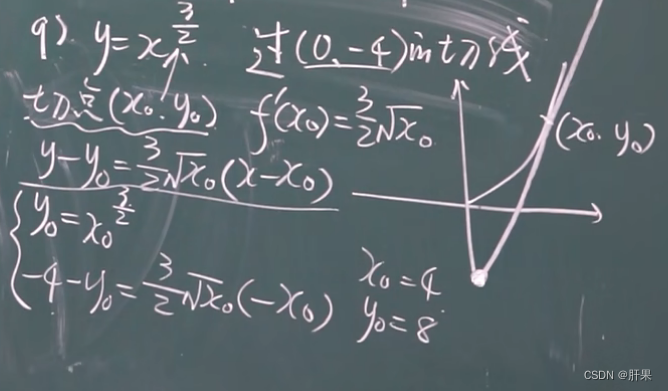

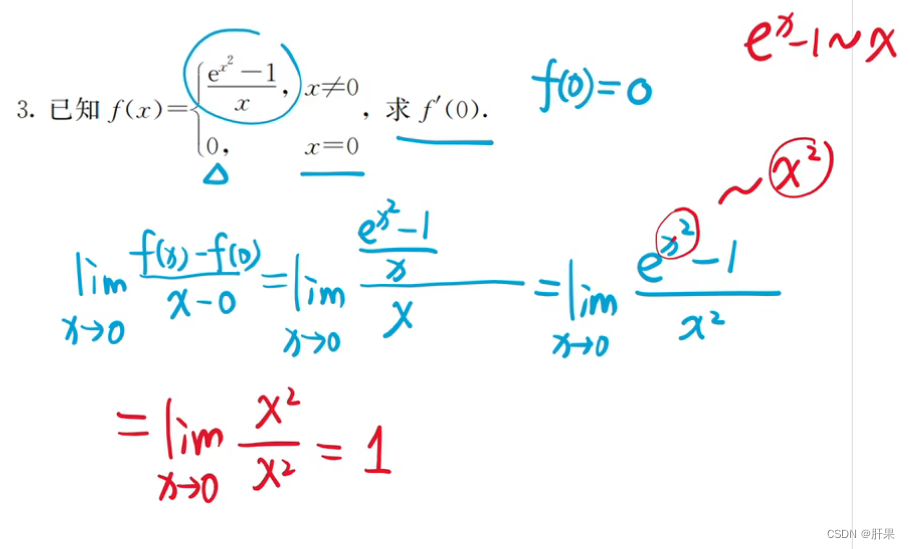

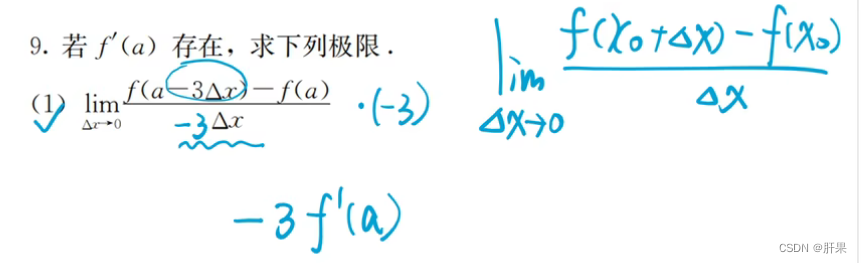



可导与连续的关系

求导法则 和差积商(本章最重要)
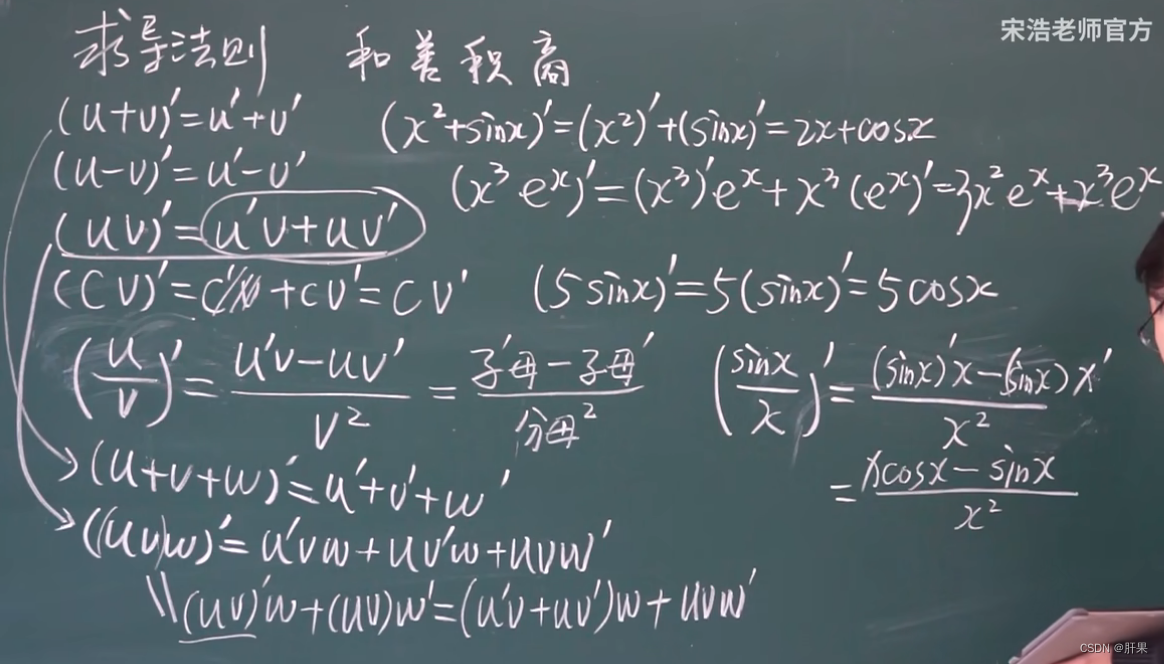

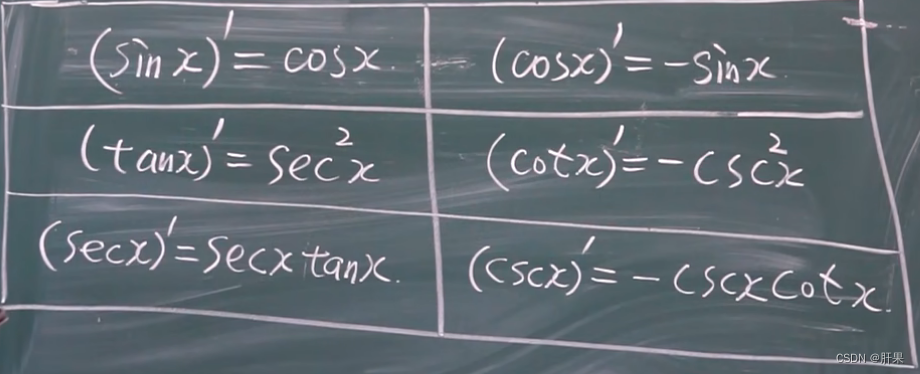

反函数的求导法则
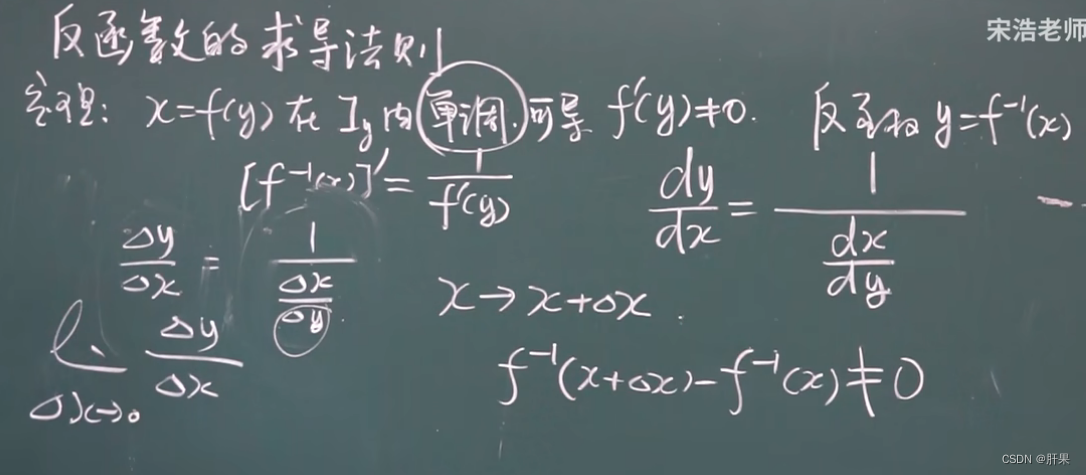
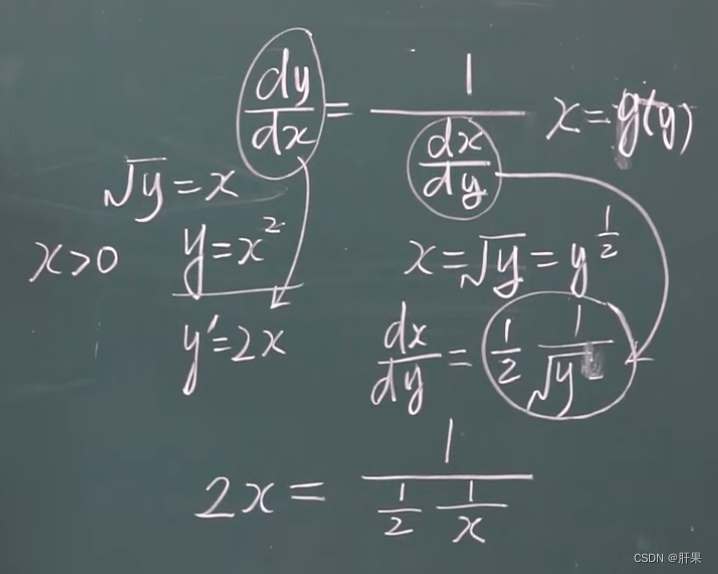

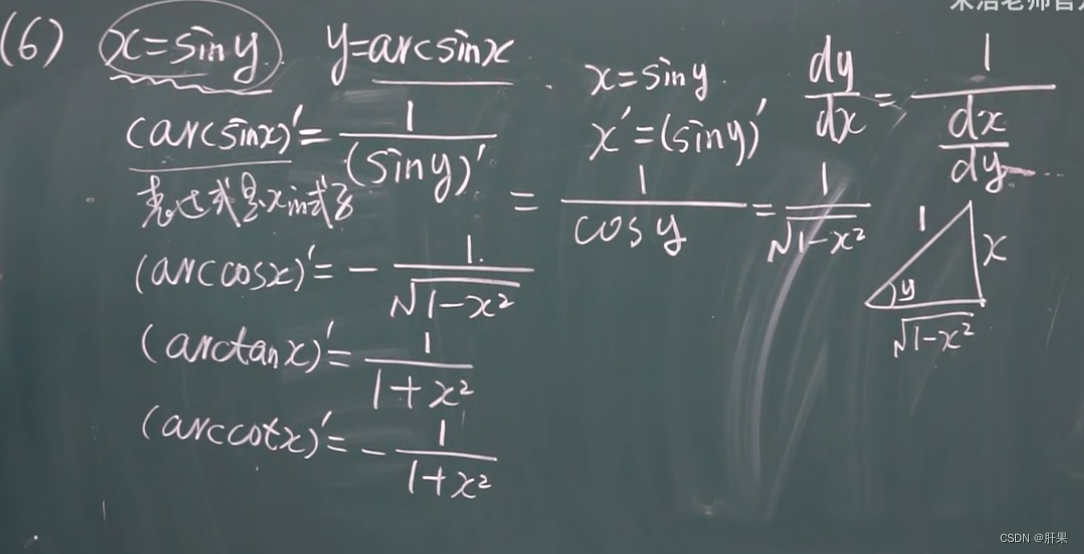
复合函数的求导(链式法则)


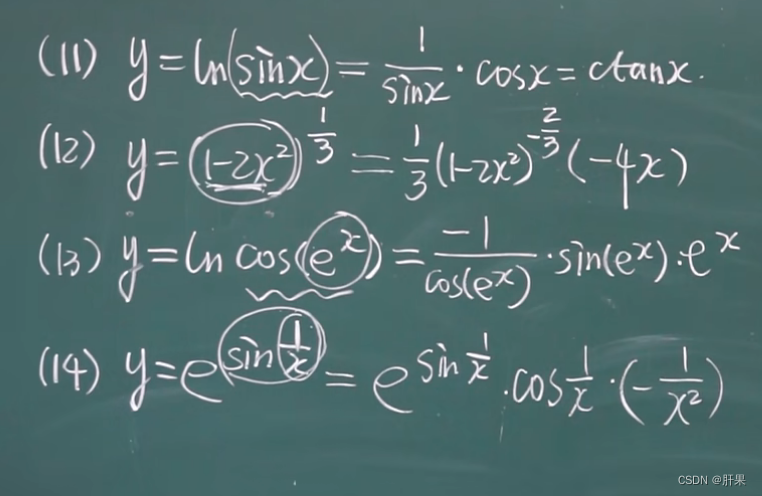
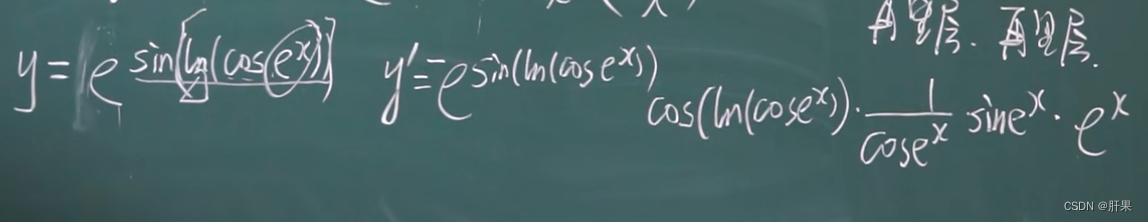
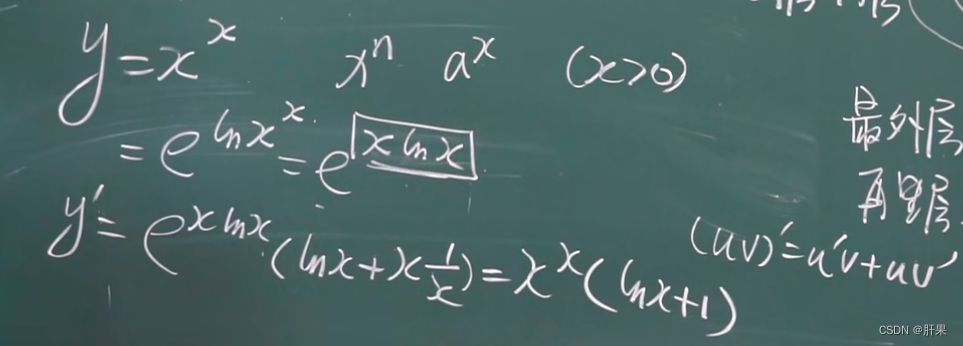
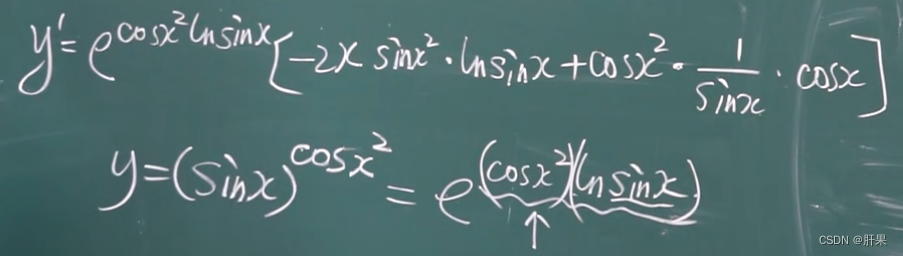
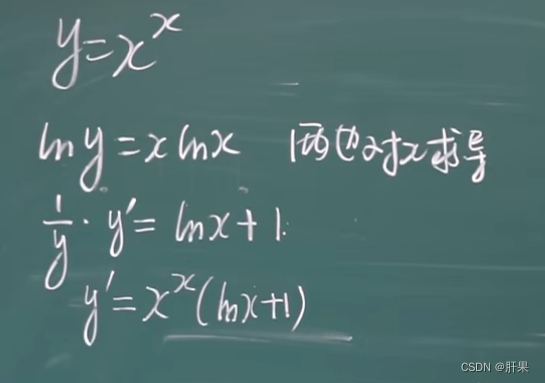
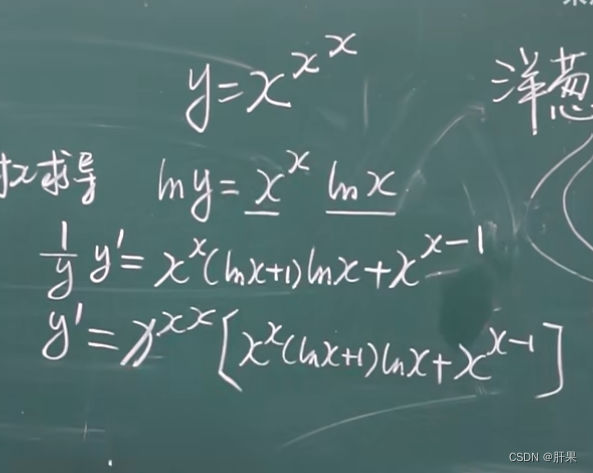
导数公式(重点)
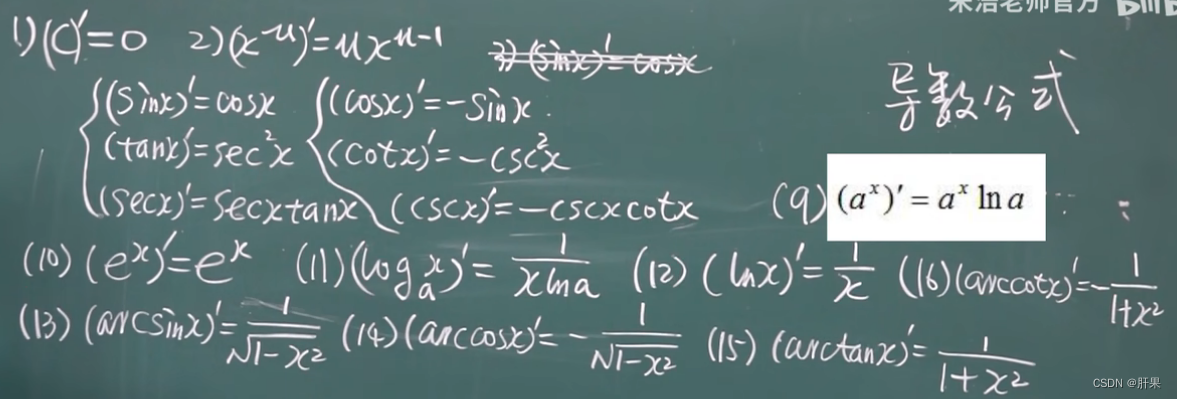
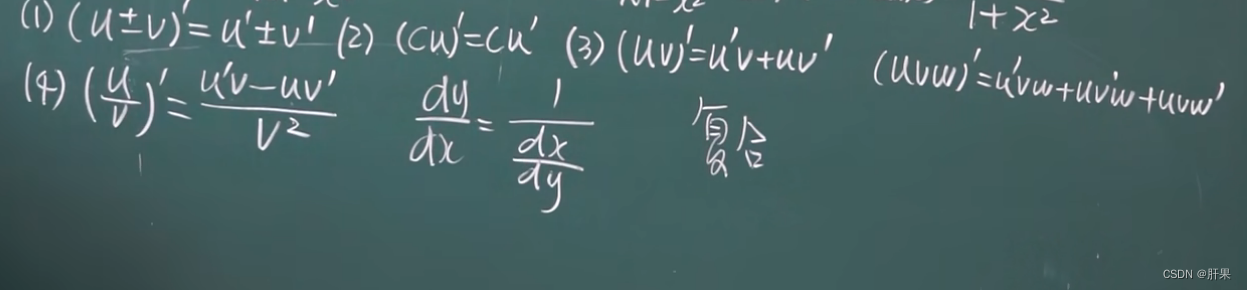
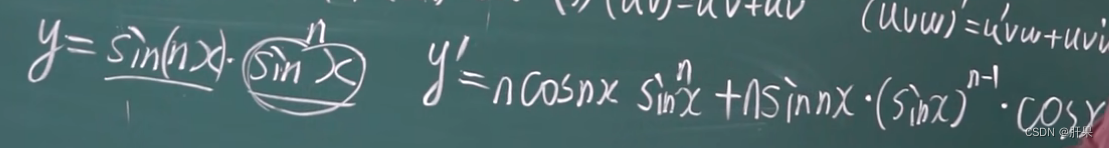
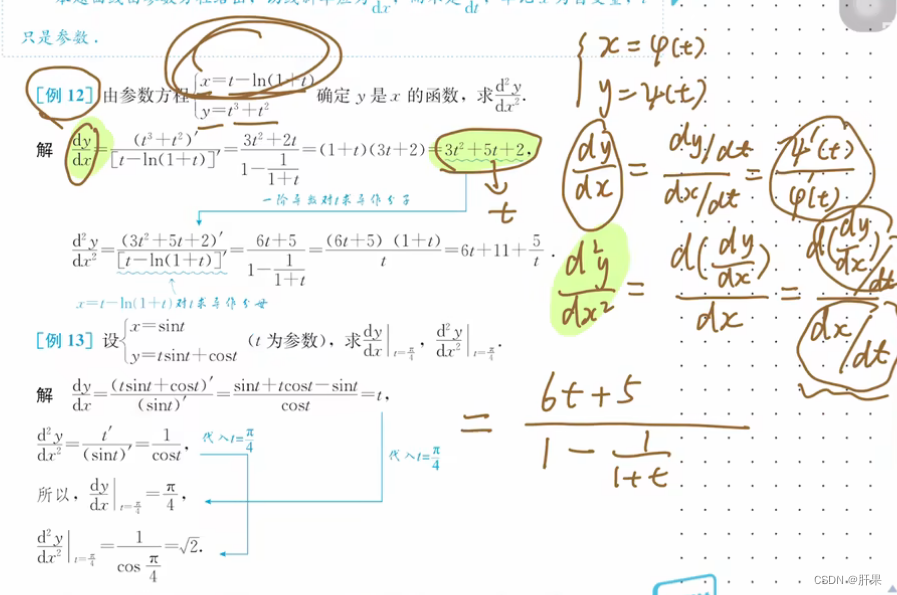
高阶导数
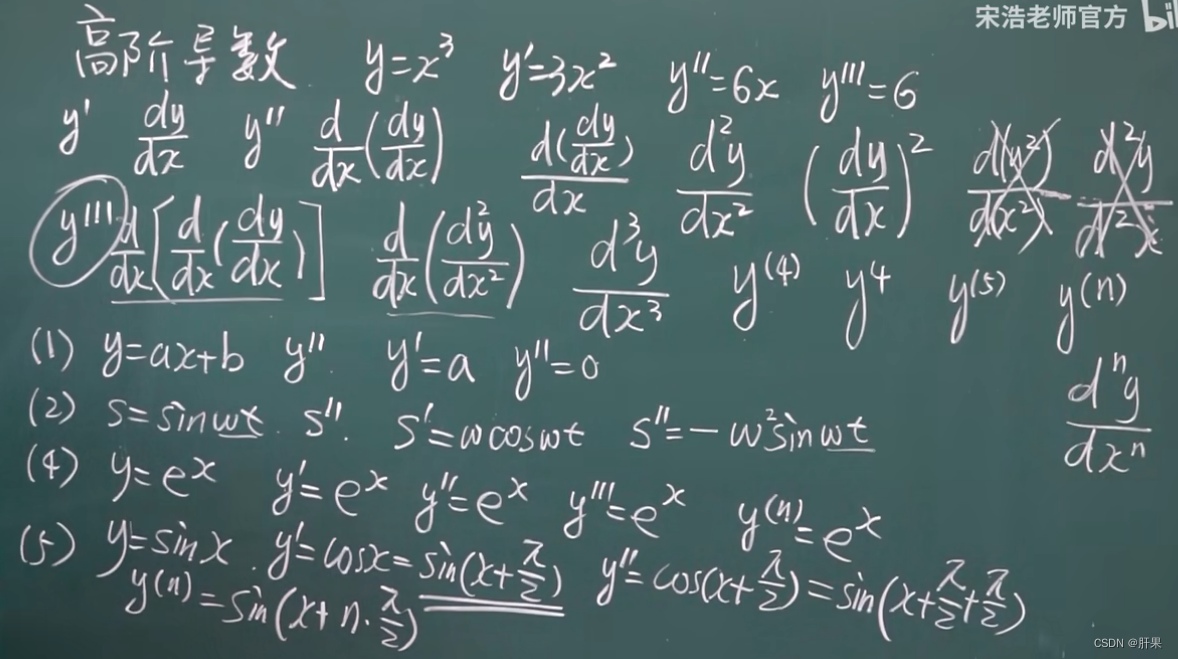
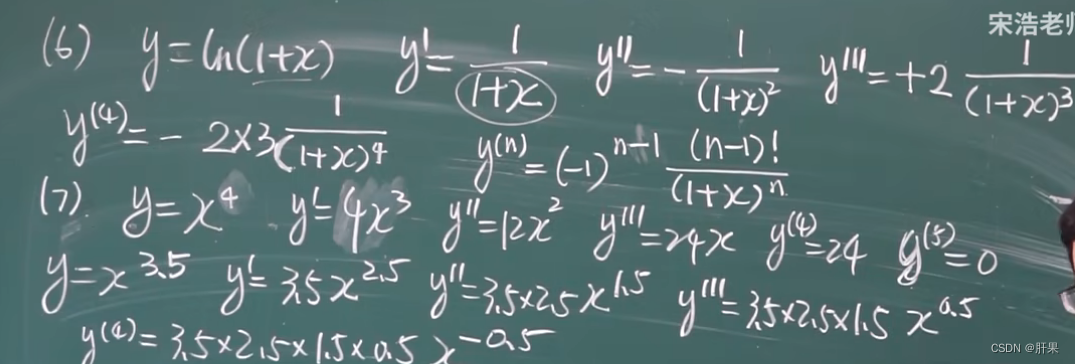
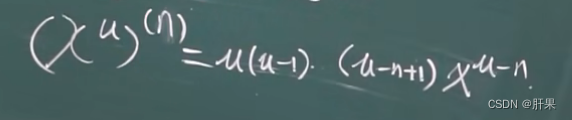
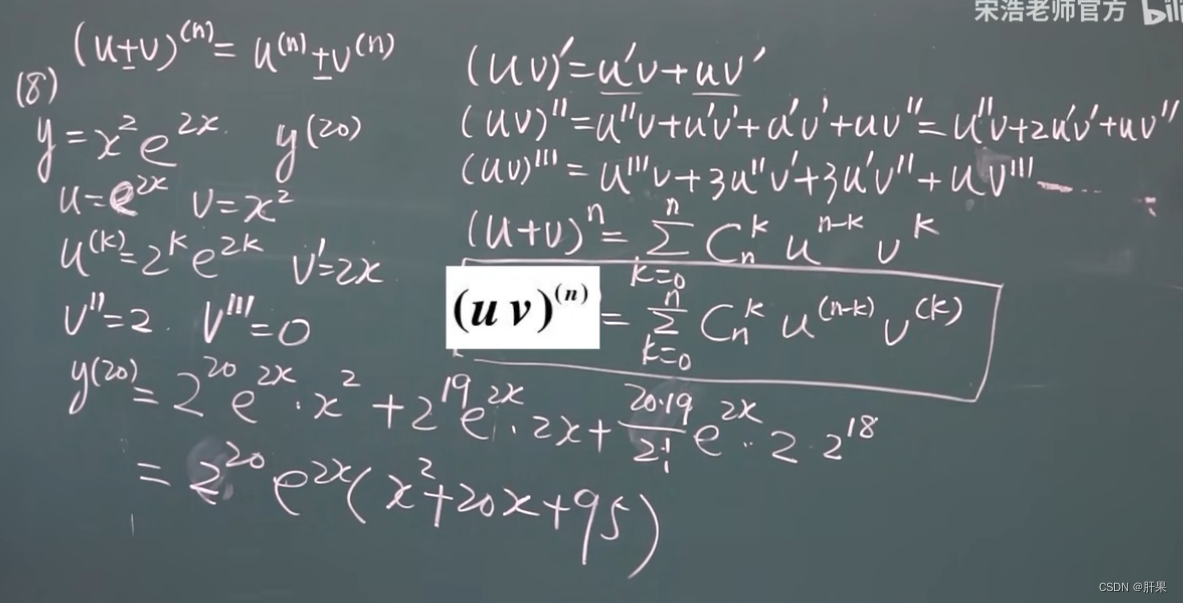
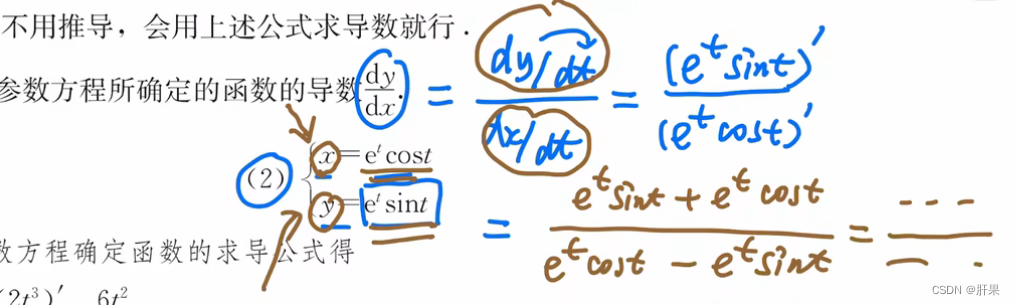
隐函数求导