神经网络
非线性假设
如果对于下图使用Logistics回归算法,如果只有x1和x2两个特征的时候,Logistics回归还是可以较好地处理的。它可以将x1和x2包含到多项式中
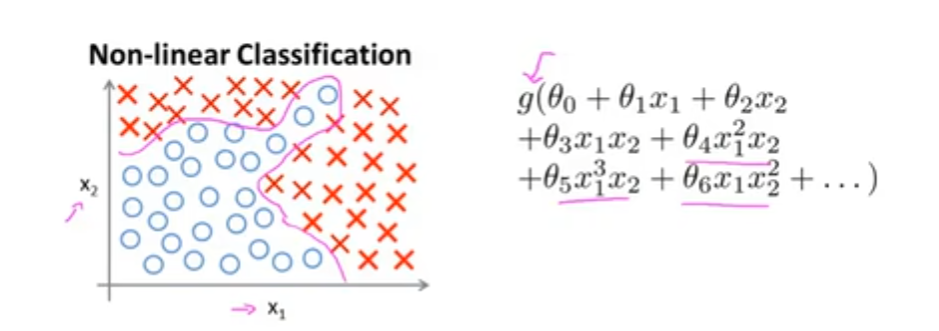
但是有很多问题所具有的特征远不止两个,甚至是上万个,如果我们想要包含很多特征,那Logistics回归的假设函数将会相当复杂。这些多项式的项数是以n^2的速度增长的。一方面运算量十分大,而且想要进行正则化调整也很难。 这么庞大的特征空间使得对特征的增删查改都十分困难,因此我们需要另寻出路。
比如,在计算机视觉中,判断一张图片是否是汽车,我们有很多图片:一些是汽车,而一些不是汽车,先取出汽车的局部特征看一下:
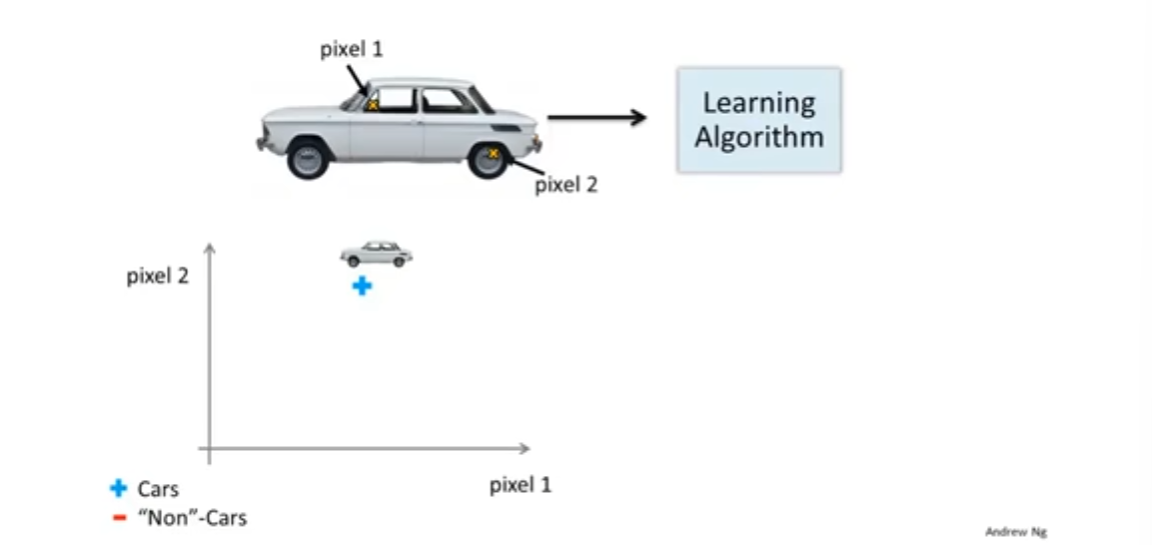
固定取出每张图片的两个固定位置的像素点pixel1和pixel2,将他们标记在以pixel1的灰阶强度为横轴、pixel2的灰阶强度为纵轴的表上,也就是将pixel1和pixel2的灰阶强度作为图片的两个特征。不断地往图表中添加数据,如下图:
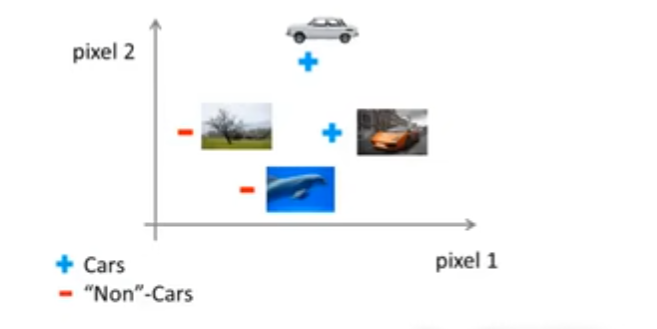
这只是两个像素之间的关系的表格,我们应该将所有像素都加入进去,假设我们的图片都是50x50像素的(这样的图片相当“马赛克”是吧!),那么就总共有2500个像素点。两个像素点之间的关系需要在一个二维表上表示,那么一个拥有2500个像素点的图片则需要在一个2500维的表上标识!换言之,如果只是两个像素,那么一个汽车图片实例的向量为
[
p
i
x
e
l
1
p
i
x
e
l
2
]
\begin{bmatrix} pixel1\\ pixel2 \end{bmatrix}
[pixel1pixel2]
而拥有2500个像素点的汽车实例的向量为
[
p
i
x
e
l
1
p
i
x
e
l
2
p
i
x
e
l
3
.
.
.
p
i
x
e
l
2500
]
\begin{bmatrix} pixel1\\ pixel2\\ pixel3\\ ...\\ pixel2500 \end{bmatrix}
pixel1pixel2pixel3...pixel2500
这里的例子一个像素还只是含有灰阶强度一个信息,这样的图片还只是黑白双色的,如果我们处理彩色图片,则需要采用RGB来表示一个像素, 那么一个像素将会携带红绿蓝三种信息。届时一张50x50的图片就拥有7500个特征!这么庞大的特征数量恐怕是传统的回归函数难以处理的
神经网络详解
神经网络的起源,是人类试图去模仿大脑的运作方式。首先我们来看一个神经元。
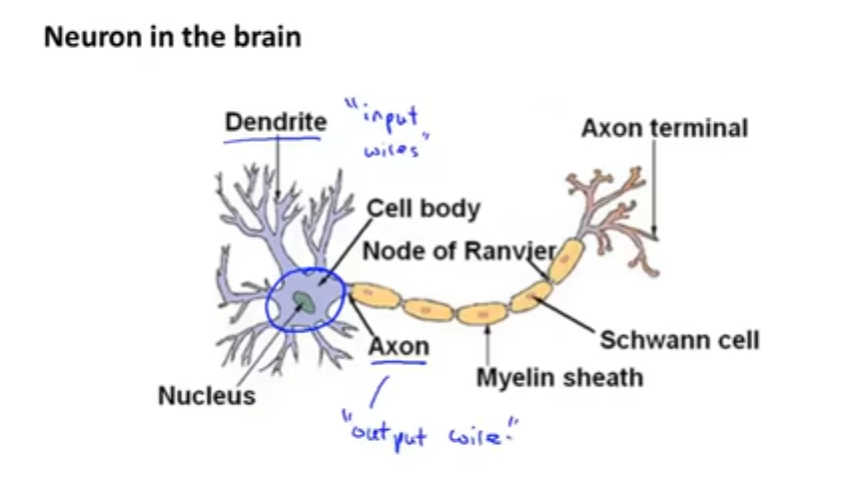
在一个神经元中,有若干个树突,树突用于向该神经元传递信息,以及有一个轴突,轴突则是该神经元向外(也就是其他神经元)传递信息,虽然只有一条轴突,但是轴突终端分出来的细支使得神经元可以同时向多个神经元传递信息。简而言之,神经元就是一个计算单元,接收了若干电信号后对电信号进行处理,并且将结果输出给其他神经元。
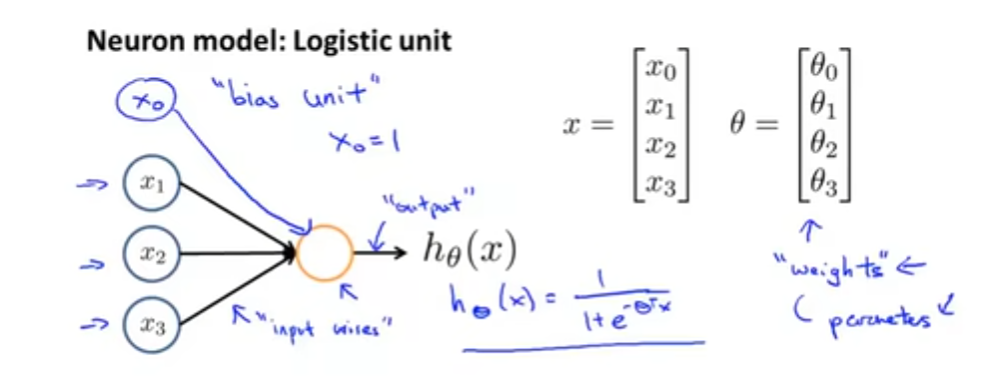
在一个神经网络里,我们将神经元的交互过程简化为一个很简单的模型,一个神经元就是一个逻辑单元。在神经网络中,激活函数就是我们曾经说的Logistic函数
g
(
z
)
=
1
/
1
+
e
−
θ
T
x
g(z)=1/1+e^{-\theta^Tx}
g(z)=1/1+e−θTx,对应的参数
θ
j
\theta_j
θj有时候也会被称之为权重
神经网络是一组神经元连接起来的组合,x1,x2,x3向第二层的神经元输入数据,然后第二层神经元处理后再向第三层的输出,如下图所示。但是需要注意的是,一般x0会被我们人为的隐藏,因为x0是固定等于1的,它不会受上一层的影响,但是会影响到下一层的结果,为什么恒为1可以看前面的线性回归内容,也可以直接私信我。

一般第一层被称之为输入层,最后一层又被称之为输出层,中间的层级被称之为隐藏层,神经网络可能会有许多层级。在深入探讨神经网络之前,我们先规定一些记号,用于后续的展开:
- a i ( j ) a_i^{(j)} ai(j)用于表示第j层第i个神经单元的激活项,表示该神经单元计算并输出的值
- Θ ( j ) \Theta^{(j)} Θ(j)表示的是权重矩阵,表示的是从第j层到第j+1层的映射,
看起来有点难懂,不如直接看下面的:
看上面的图可以知道
a
1
(
2
)
a_1^{(2)}
a1(2)也就是第二层第一个激活值是和第一层的x1,x2,x3有关的,实际上他的式子如下
a
1
(
2
)
=
g
(
z
1
(
2
)
)
=
g
(
Θ
10
(
1
)
x
0
+
Θ
11
(
1
)
x
1
+
Θ
12
(
1
)
x
2
+
Θ
13
(
1
)
x
3
)
a_1^{(2)} = g(z_1^{(2)})=g(\Theta_{10}^{(1)}x_0+\Theta_{11}^{(1)}x_1+\Theta_{12}^{(1)}x_2+\Theta_{13}^{(1)}x_3)
a1(2)=g(z1(2))=g(Θ10(1)x0+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3)
其中
Θ
10
(
1
)
\Theta_{10}^{(1)}
Θ10(1)表示的是从x0映射到第二层第一个节点
a
1
(
2
)
a_1^{(2)}
a1(2)的权重,函数g(z)是Logistic函数
照猫画虎我们还可以写出如下的内容:
a
2
(
2
)
=
g
(
z
2
(
2
)
)
=
g
(
Θ
20
(
1
)
x
0
+
Θ
21
(
1
)
x
1
+
Θ
22
(
1
)
x
2
+
Θ
23
(
1
)
x
3
)
a_2^{(2)} = g(z_2^{(2)})=g(\Theta_{20}^{(1)}x_0+\Theta_{21}^{(1)}x_1+\Theta_{22}^{(1)}x_2+\Theta_{23}^{(1)}x_3)
a2(2)=g(z2(2))=g(Θ20(1)x0+Θ21(1)x1+Θ22(1)x2+Θ23(1)x3)
a
3
(
2
)
=
g
(
z
3
(
2
)
)
=
g
(
Θ
30
(
1
)
x
0
+
Θ
31
(
1
)
x
1
+
Θ
32
(
1
)
x
2
+
Θ
33
(
1
)
x
3
)
a_3^{(2)} = g(z_3^{(2)})=g(\Theta_{30}^{(1)}x_0+\Theta_{31}^{(1)}x_1+\Theta_{32}^{(1)}x_2+\Theta_{33}^{(1)}x_3)
a3(2)=g(z3(2))=g(Θ30(1)x0+Θ31(1)x1+Θ32(1)x2+Θ33(1)x3)
如果你学习过线性代数就知道,方程组和矩阵是可以相互转化的,我们将这个方程组中的参数 Θ \Theta Θ转化为矩阵形式就可以得到一个3行4列矩阵
Θ
(
1
)
=
[
Θ
10
(
1
)
Θ
11
(
1
)
Θ
12
(
2
)
Θ
13
(
1
)
Θ
20
(
1
)
Θ
21
(
1
)
Θ
22
(
2
)
Θ
23
(
1
)
Θ
30
(
1
)
Θ
31
(
1
)
Θ
32
(
2
)
Θ
33
(
1
)
]
\Theta^{(1)} = \begin{bmatrix} \Theta_{10}^{(1)}& \Theta_{11}^{(1)} & \Theta_{12}^{(2)} &\Theta_{13}^{(1)}\\ \Theta_{20}^{(1)}& \Theta_{21}^{(1)} & \Theta_{22}^{(2)} &\Theta_{23}^{(1)}\\ \Theta_{30}^{(1)}& \Theta_{31}^{(1)} & \Theta_{32}^{(2)} &\Theta_{33}^{(1)}\\ \end{bmatrix}
Θ(1)=
Θ10(1)Θ20(1)Θ30(1)Θ11(1)Θ21(1)Θ31(1)Θ12(2)Θ22(2)Θ32(2)Θ13(1)Θ23(1)Θ33(1)
这个就是我们所说的权重矩阵
接下来我们讨论下神经网络的向量化。上面的方程组可以简写为
a
1
(
2
)
=
g
(
z
1
(
2
)
)
a_1^{(2)} = g(z_1^{(2)})
a1(2)=g(z1(2))等,因此我们可以将特征向量x定义为
x
=
[
x
0
x
1
x
2
x
3
]
x=\begin{bmatrix} x_0\\ x_1\\ x_2\\ x_3 \end{bmatrix}
x=
x0x1x2x3
将权重矩阵定义为
KaTeX parse error: Expected '}', got '\end' at position 63: …\ z_3^{(2)}\\ \̲e̲n̲d̲{bmatrix}
拥有了向量化的神经网络后,我们可以使用向量一次性处理大量数据,比如我想求出第二层节点
a
(
2
)
a^{(2)}
a(2)的值,则使用
z
(
2
)
=
Θ
(
1
)
x
,
a
(
2
)
=
g
(
z
(
2
)
)
z^{(2)}=\Theta^{(1)}x,a^{(2)}=g(z^{(2)})
z(2)=Θ(1)x,a(2)=g(z(2))