https://blog.csdn.net/weixin_45434953/article/details/130970273
上一篇文章的例子中，如果使用一个四次多项式去拟合房价函数，会导致过拟合问题

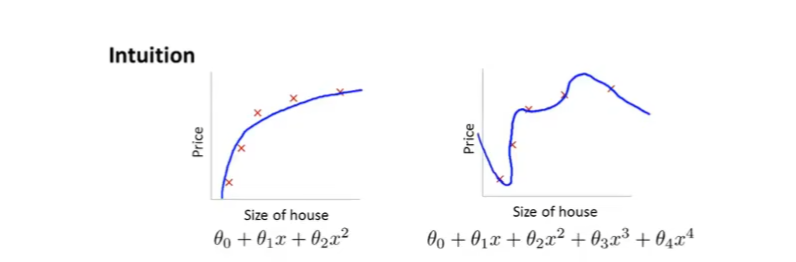
而正则化是解决过拟合的一个方法。右图过拟合是因为其三次方项和四次方项的影响，我们再回顾下线性回归的代价函数：
$$J=\frac{1}{2m}\sum _{i=1}^m{h}_{\theta }(x^{(i)}-y^{(i)}{)}^2$$我们可以人为地添加一些"惩罚项"，比如：$$J=\frac{1}{2m}\sum _{i=1}^m{h}_{\theta }(x^{(i)}-y^{(i)}{)}^2+1000{\theta }_3^2+1000{\theta }_4^2$$当我们要得出最小的代价函数的时候，${\theta }_3$和${\theta }_4$必须要尽可能接近于0，否则函数J会变得很大。对于假设函数${\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2+{\theta }_3{x}^3+{\theta }_4{x}^4$来说${\theta }_3$和${\theta }_4$接近于0会使得函数图像较为接近${\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2$，但是仍然保留有${\theta }_3$和${\theta }_4$的特征，而不是简单地将它抛弃掉

简单来说，正则化能够在不丢失特征信息的情况下简化模型，使得曲线更加平滑而非“放飞自我”。假设房价有101个特征：${\theta }_0......{\theta }_{1}00$那么我们也能使用如下的正则化方式:$$J=[\frac{1}{2m}\sum _{i=1}^m{h}_{\theta }(x^{(i)}-y^{(i)}{)}^2+\lambda \sum _{j=1}^m{\theta }_j^2]$$可以看到我们一般不对${\theta }_0$进行正则化。其中$\lambda$用于控制它们之间的权重。如果$\lambda$太大，会使得函数假设函数近似于${\theta }_0$也就是用一条直线去拟合，反而变成了欠拟合了，因此对$\lambda$也需要小心设置。

线性回归正则化

对于正则化的线性回归，我们需要作如下修改-
仔细观察可知道，粉色括号里的项恰好是正则化后的代价函数$J(\theta )$的导数。我么不妨整理一下$${\theta }_j:=(1-\partial \frac{\lambda }{m}){\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\ast x^{(i)}$$可以看到，正则化的梯度下降就是将${\theta }_j$缩小一下，然后采用常规的梯度下降进行处理

如果我们采用正规方程，那么正则化的正规方程的形式则如下：
$$\theta =(X^{T}X+\lambda \left[\begin{array}{ccccc}0& & & & \\ & 1& & & \\ & & .& & \\ & & & .& \\ & & & & 1\end{array}\right]{)}^{-1}{X}^{T}y$$
相比常规正规方程增加了一个矩阵后，只要$\lambda >0$小括号里的矩阵就一定是可逆的，因此是一定有计算结果的。这也回应了之前在介绍正规方程时，$(X^{T}X{)}^{-1}{X}^{T}y$中的矩阵求逆一旦遇到不可逆的矩阵该怎么办，答案就是采用正规化将其变成可逆的

逻辑(Logistics)回归正规化

当我们采用一个有很多无关特征的多项式进行拟合的时候，这些大量的特征会导致过拟合