算法的重构是压缩感知中重要的一步，是压缩感知的关键之处。因为重构算法关系着信号能否精确重建，国内外的研究学者致力于压缩感知的信号重建，并且取得了很大的进展，提出了很多的重构算法，每种算法都各有自己的优缺点，使用者可以根据自己的情况，选择适合自己的重构算法，大大增加了使用的灵活性，也为我们以后的研究提供了很大的方便。

压缩感知的重构算法主要分为三大类：

1.组合算法   2.贪婪算法  3.凸松弛算法

每种算法之中又包含几种算法，下面就把三类重构算法列举出来。

算法类别	定义	优缺点	具体算法
贪婪算法	贪婪算法首先选取合适的原子，再逐步进行递增，进而逼近信号矢量，利用这种过程进行	计算量和精度的要求居中，也是三种重构算法中应用最大的一种	(1)匹配追踪算法 (2)正交匹配追踪算法 (3)分段正交匹配追踪算法 (4)正则化正交匹配追踪算法 (5)稀疏自适应匹配追踪算法
组合算法	先是对信号进行结构采样，然后再通过对采样的数据进行分组测试，最后完成信号的重构	需要观测的样本数目比较多但运算的效率最高	(1) 傅里叶采样 (2) 链式追踪算法 (3)  HHS追踪算法
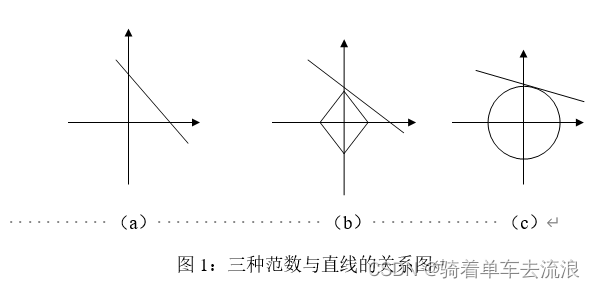
凸松弛算法	法，它将非凸问题转化为凸问题进行求解，即l0范数转化成l1范数并采用线性规划来求解	计算量大但是需要观测的数量少重构的时候精度高	(1)基追踪算法 (2)最小全变差算法 (3)内点法 (4)梯度投影算法 (5)凸集交替投影算法

本篇主要阐述分段正交匹配追踪算法

分段正交匹配追踪(Stagewise OMP)也是由OMP改进而来的一种贪心算法，与CoSaMP、SP算法类似，不同之处在于CoSaMP、SP算法在迭代过程中选择的是与信号内积最大的2K或K个原子，而StOMP是通过门限阈值来确定原子。此算法的输入参数中没有信号稀疏度K，因此相比于ROMP及CoSaMP有独到的优势。

StOMP的算法流程：

 

 

 StOMP的算法结果：