2000-2020全要素生产率OP法+LP法+OLS和固定效应法三种方法合集含原始数据和计算过程Stata代码

1、时间：OP法：2008-2020年、LP法2000-2020年、OLS和固定效应法2000-2020年

2、数据内容：包括原始数据、计算结果和stata do文档

3、方法说明：

Olley-Pakes法（简称OP法）鉴于固定效应方法存在以上自身难以克服的问题，Olley and Pakes（1996）发展了基于一致半参数估计值方法（Consistenesemi-parametricesti-mator）。该方法假定企业根据当前企业生产率状况，据此做出投资决策，因此用企业的当期投资作为不可观测生产率冲击的代理变量，从而解决了同时性偏差问题。
OLS法：如果有充足的理由相信影响企业决策的那部分可观测的TFP是因企业而异的，而且是跨时不变的，那么在面板数据条件下，一个相对简单的方法是使用个体固定效应回归方法估计。
Levinsohnand Petrin（简称LP法） 在满足一系列假定的条件下，Olley-Pakes方法可以提供对企业层生产函数的一致估计值。其中一个假定是要求代理变量 （投资）与总产出始终保持单调关系。这就意味着那些投资额为零的样本并不能被估计。事实上，由于并非每一个企业每一年都有正的投资，从而使得很多企业样本在估计过程中被丢弃掉了。Levinsohnand Petrin(2003)针对这一问题发展了一种新的全要素生产率估计方法。该方法并不是使用投资额作为代理变量，而是代之以中间 品投入指标，从数据的角度出发，中间品投入更易获得。

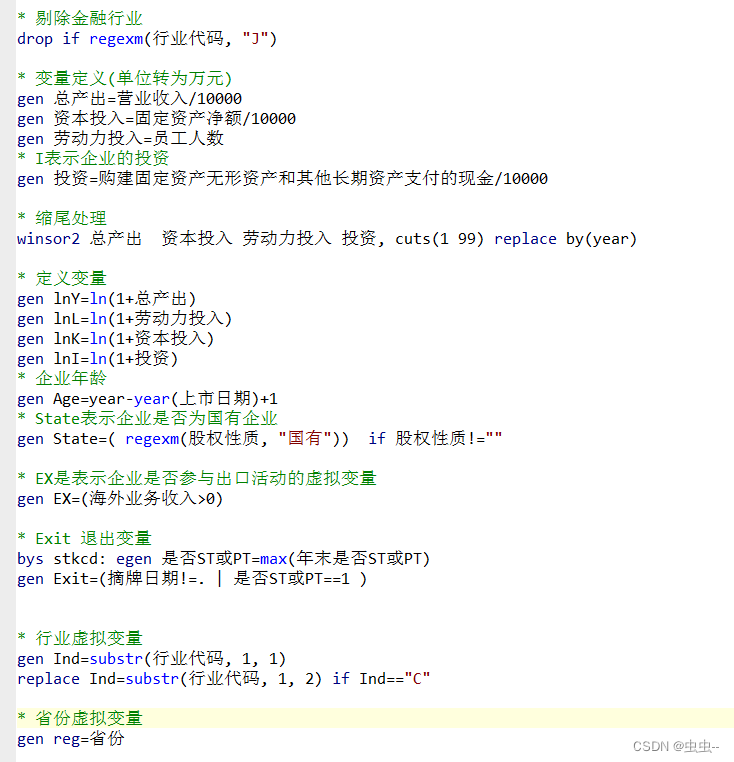
4、部分代码:

OP方法计算
* 安装opreg， 输入命令findit opreg找到对应命令进行安装
xtset stkcd year
xi: opreg lnY, exit(Exit) state(Age lnK) proxy(lnI) free(lnL i.Ind i.year i.reg) cvars(State EX )   vce(bootstrap, seed(1357) rep(5)) 
est store OP

gen tfp_op=lnY - _b[lnL]*lnL-_b[lnK]*lnK

keep stkcd 证券代码 year tfp_op
save 运行结果.dta, replace
export excel 结果导出.xlsx, firstrow(var) replace

下载链接：

2000-2020全要素生产率OP法+LP法+OLS和固定效应法-文献-数据-Statahttps://download.csdn.net/download/m0_71334485/85927928