文章及补充材料链接:https://jguan.page/Radatron/
理解本文需要一些电磁波与雷达信号处理相关的理论知识。
1. 引言
雷达的角度分辨率通常很低。雷达的角度分辨率与雷达的天线孔径成反比,因此毫米波雷达要达到激光雷达的角度分辨率,需要3000根天线,10m孔径。另一增大角度分辨率的方法是使用级联MIMO雷达模拟大孔径雷达,其中雷达轮流发射信号以避免干扰。将多个收发器的信号进行组合,可以生成高精度雷达图像。但这种方法对于自动驾驶中的动态场景不适用,因为每个雷达采集的时间不同,场景存在差异。这在视觉中会导致运动模糊,但容易去除;而毫米波雷达的射频信号属于毫米波长的正弦波,一个微小运动就会改变发射器信号的符号,从而在结合后导致模糊、失焦甚至消除物体,且这种影响会随发射器数量的增大而增大。
本文的方法通过使用一种新型雷达数据预处理方法和深度学习网络来克服上面的问题。前者能补偿运动引起的大部分误差,而剩下的误差来自相对速度较大的场景。本文使用一个两分支的神经网络,将高分辨率和低分辨率的雷达图像作为输入,使用无运动误差的低分辨率图像纠正高分辨率图像中的错误信息。
本文介绍了一个包含级联MIMO雷达数据的数据集Radatron,其中雷达信号的水平角分辨率是普通雷达的10倍(
1.
8
∘
1.8^\circ
1.8∘)。实验表明本文获取的高精度雷达数据能大幅提高检测性能,尤其是对于对向来车等困难情况。
2. 相关工作
一些数据集使用雷达点云,但过滤算法会导致有效信息的损失和雷达点云的稀疏性。Radatron提供的是3D雷达热图。
3. 毫米波MIMO雷达的背景知识
毫米波雷达发射调频连续波(FMCW)来感知环境。发射天线(TX)发射信号在物体上反射,然后被接收天线(RX)接收。比较发射和接收信号,可以得到往返飞行时间(ToF)
τ
\tau
τ,从而得到物体的距离
ρ
=
τ
c
/
2
\rho=\tau c/2
ρ=τc/2(
c
c
c为光速)。使用多个RX接收信号,ToF之差可以用于估计反射波到达的角度
ϕ
\phi
ϕ。
(
ρ
,
ϕ
)
(\rho,\phi)
(ρ,ϕ)就建立了雷达热图,可在2D极坐标下定位物体。
雷达的距离分辨率与FMCW波的带宽成正比,而角度分辨率与RX的数量成正比。毫米波频段的带宽较高,因此毫米波雷达的距离分辨率可达厘米级。但要增大角度分辨率,通过增大RX的数量来实现是不现实的;一个可行方案是使用多个TX和多个RX组成的MIMO雷达。设
N
N
N个TX轮流发射信号,
M
M
M个RX进行接收,可以仅使用
N
+
M
N+M
N+M个物理天线模拟
N
×
M
N\times M
N×M个虚拟天线。
N
×
M
N\times M
N×M个虚拟天线的接收信号组合起来,就能建立
(
ρ
,
ϕ
)
(\rho,\phi)
(ρ,ϕ)热图。
由于TX轮流发射信号,第
i
i
i个天线和第
j
j
j个天线发射信号会存在微小时间差
δ
t
i
j
\delta t_{ij}
δtij。静止场景中这个时间差是无害的,但对于运动场景,即使只有1mm的变化,角度估计也会明显变化,这是因为
δ
t
i
j
\delta t_{ij}
δtij内的运动污染了ToF差值
Δ
τ
i
j
\Delta\tau_{ij}
Δτij:
Δ
τ
i
j
′
=
τ
i
−
τ
j
+
δ
t
i
j
2
v
c
=
Δ
τ
i
j
+
δ
t
i
j
2
v
c
\Delta\tau'_{ij}=\tau_i-\tau_j+\delta t_{ij}\frac{2v}{c}=\Delta\tau_{ij}+\delta t_{ij}\frac{2v}{c}
Δτij′=τi−τj+δtijc2v=Δτij+δtijc2v其中
v
v
v是相对速度,
c
c
c为光速;且
v
v
v越大,误差越大。这会导致雷达热图中的物体反射被污染,例如移动到另一个位置或是分裂为多个不同角度、不太明显的反射。
4. 方法
4.1 雷达信号处理
本文设计运动补偿算法,并整合到雷达数据处理流程中,如图所示。

首先输入原始雷达信号,在时域使用标准的快速傅里叶变换,以估计不同距离的反射强度。在估计反射角度前,先利用虚拟天线阵列的冗余性,补偿运动引入的失真。设
i
i
i与
i
′
i'
i′是co-located的虚拟天线对(
τ
i
=
τ
i
′
\tau_i=\tau_{i'}
τi=τi′),估计的ToF差值为
τ
i
−
τ
i
′
+
δ
t
i
i
′
2
v
c
=
δ
t
i
i
′
2
v
c
\tau_i-\tau_{i'}+\delta t_{ii'}\frac{2v}{c}=\delta t_{ii'}\frac{2v}{c}
τi−τi′+δtii′c2v=δtii′c2v,其中
v
v
v为唯一的未知数,可以估计得到,进一步得到运动引入失真,将其相反数添加到所有的TX上进行补偿(具体算法见附加材料)。最后,使用纠正的
δ
τ
\delta\tau
δτ提取反射角度信息。使用传统波束形成算法得到极坐标下的2D距离-水平角(RA)雷达热图,其每个像素值代表反射强度。将这一雷达信号处理流程用于生成网络的两个输入:
高分辨率级联雷达:使用多个TX以获得较高的角度分辨率。
低分辨率单一雷达:使用一个TX和全部RX,无需运动补偿,但导致角度分辨率低、引入泄漏伪影。
4.2 Radatron网络设计
经过上述预处理,仍可能有少数困难情况(如对向来车)可能存在误差。为结合级联雷达与单一雷达的优势,Radatron将两者融合,使用Fast R-CNN FPN结构。
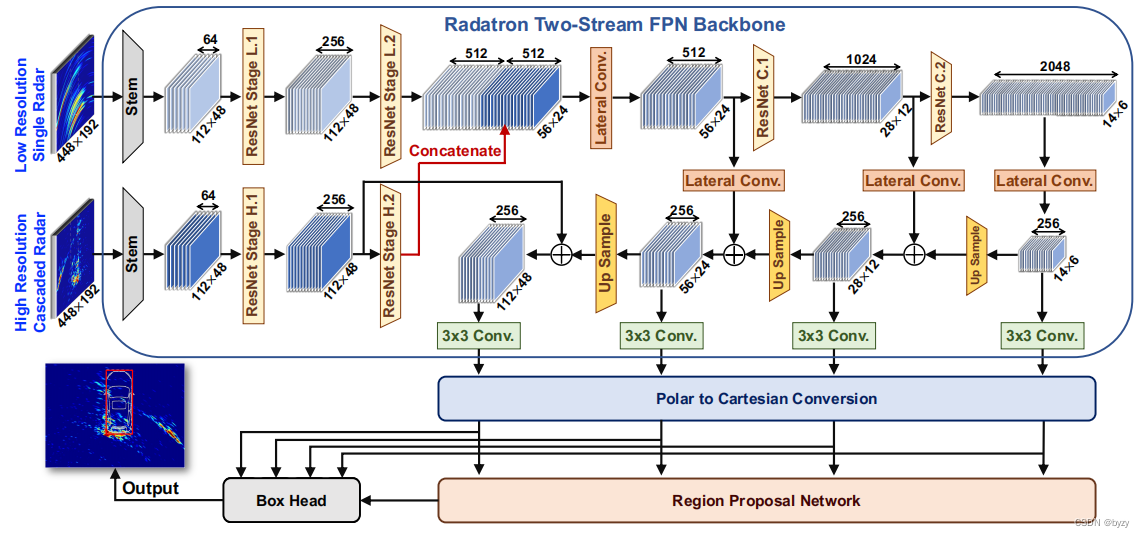
如图所示,一个分支使用低分辨率单一雷达热图,用其无污染的特点检测高动态物体;另一分支使用高分辨率级联雷达热图精确捕捉汽车轮廓。在主干网络中间层深度融合两者特征,最后将极坐标转换到直角坐标,输入到RPN和ROI头中,得到2D边界框。
Radatron的主干网络:使用基于FPN的结构,输入为相同尺寸的热图,使用两个相同的分支处理:首先通过Stem层(
7
×
7
7\times7
7×7卷积+ReLU+BN)然后通过ResNet,拼接后使用
3
×
3
3\times3
3×3卷积融合。最后再通过ResNet层进一步编码特征图并组合。
坐标转换:极坐标是雷达信号的自然表达,但边界框更适合在笛卡尔坐标下表达,因此本文在主干网络使用极坐标,而在后续的RPN和ROI头使用直角坐标(通过双线性插值得到)。
数据增广:训练时,使用角度翻转(即水平翻转,以消除数据集内在偏差;原始数据多数车辆出现在自车一侧)和角度平移(即绕原点旋转,以生成更多朝向的边界框;原始数据多数车辆的朝向与自车相同或相反)。
6. 评估和实验
评估指标:
A
P
0.5
AP_{0.5}
AP0.5、
A
P
0.75
AP_{0.75}
AP0.75和不同IoU阈值下AP的均值mAP。
基准方案:(1)模拟其余数据集的虚拟天线阵列(仅产生低分辨率雷达数据);(2)只有低分辨率单一雷达热图分支的Radatron;(3)高分辨率级联雷达热图不进行运动补偿预处理,输入到只有高分辨率级联雷达热图分支的Radatron中;(4)使用雷达单一模态版本的MVDNet(输入为高分辨率级联雷达热图,进行/不进行运动补偿预处理),与仅有高分辨率级联雷达热图分支的Radatron进行比较。
测试集分割:将测试集的数据分为3类,即同向(同一车道、朝向角小于
5
∘
5^\circ
5∘的车辆)、有偏(同一车道、朝向角大于
5
∘
5^\circ
5∘的车辆)和对向(对向车道的车辆),对于高分辨率级联雷达热图来说依次是简单、中等和困难难度。
6.1 与基准方案比较
与基准方案(1)比较,实验结果表明使用本文角度分辨率更高的雷达数据在所有评估指标上均更高,且越困难的样本、IoU阈值越大的AP提升越大。这被归因于运动补偿算法、多分辨率网络和数据集的高分辨率热图。
与基准方案(2)(3)比较,本文的方法有更好的性能,特别是对于困难样本。在有偏车辆的检测上,Radatron性能优于基准方案(2),因为低分辨率和高泄漏率使得确定物体朝向很困难;在对向来车的检测上,Radatron性能优于基准方案(3),因为运动补偿的缺失使得热图有严重失真。
与基准方案(4)比较,尽管运动补偿能大幅提高MVDNet对对向来车的检测性能,但Radatron仍大幅优于之。这被归因于Resnet FPN主干结构和极坐标到笛卡尔坐标的转换。
6.2 Radatron的性能
实验表明本文的运动补偿和多分辨率网络均有帮助。但对于有偏车辆来说,使用多分辨率带来的性能提升会比对向来车更小。
6.3 定性结果
随着雷达分辨率的提高,检测精度也会提高,特别是对于有偏车辆。但相同分辨率下,无运动补偿的热图受到运动引入失真的影响而对高速物体(如对向来车)的检测较差。失效情况表明网络有时候会错误地信任低分辨率输入并视图处理不存在的运动失真。
本文还使用雾机模拟真实的雾,并在此情况下进行检测。结果表明即使图像完全看不见车辆,雷达也能准确地检测到物体。
7. 局限性与讨论
Radatron数据集的最大检测范围仅有25m;Radatron网络仅处理了2D雷达数据,而使用3D数据可以估计3D边界框;多普勒信息也可被利用;训练集和测试集来自同一国家,泛化性有待考量;Radatron数据集目前仅包含车辆检测。
附:补充材料
附录B: 消融研究
数据增广的影响:去掉4.2节中的数据增广后有,对有偏车辆和对向来车的检测分别有较大性能下降,证实了本文提出的两种数据增广的作用。
坐标系的影响:使用两种变体进行实验(笛卡尔输入、隐式地学习坐标变换)。Radatron的方法比笛卡尔输入有更好的性能,证实了在极坐标下,网络更容易学习和抑制雷达伪影。Radatron的性能也比隐式地学习坐标变换更好。
在不同阶段融合:与输入融合(融合后通过所有ResNet)和晚期融合(分别通过所有ResNet后融合)比较,Radatron均有更好的性能。
多普勒:本文提取单一TX的多普勒信息,作为Radatron单一TX输入的另一通道(多普勒预处理算法见附录G)。实验表明如此使用多普勒信息不会带来性能提升。可能的原因是,尽管多普勒信息对分辨不同速度、相距较近的汽车有帮助,但这不是本文主要的误差来源(运动引入失真)。
附录C: 失效情况分析
- 遮挡:导致漏检或边界框错位;
- 镜面反射:一部分雷达信号不能被反射回雷达接收器,导致边界框大小或位置误差较大;
- 对背景的误检:如房屋等;
- 相邻汽车:将两辆相邻纵向汽车识别为一辆横向汽车;或反过来;
- 视野边缘的低分辨率:雷达的角度分辨率是中间高两侧低的;距离越远空间分辨率越低。
附录E: 运动引入失真的数学表达
雷达射频信号ToF的差异将转化为相位差。两个天线之间存在ToF差异的原因有两点:一是天线之间微小的位置差异(
Δ
τ
i
j
\Delta \tau_{ij}
Δτij),二是环境中物体的运动(
δ
t
i
j
2
v
c
\delta t_{ij}\frac{2v}{c}
δtijc2v)。
相量表示:毫米波雷达发射的电磁波是正弦波,即
Signal
=
A
sin
(
2
π
f
t
+
θ
0
)
\textup{Signal}=A\sin(2\pi ft+\theta_0)
Signal=Asin(2πft+θ0)其中
A
A
A为振幅,
f
f
f为频率,
θ
0
\theta_0
θ0为初相,
2
π
f
t
+
θ
0
2\pi ft+\theta_0
2πft+θ0为瞬时相位。相应的相量为
Phasor
=
A
e
j
(
2
π
f
t
+
θ
0
)
\textup{Phasor}=Ae^{j(2\pi ft+\theta_0)}
Phasor=Aej(2πft+θ0) FMCW波雷达信号的频率随时间线性变化,则其相量表示为
FMCW
=
A
e
j
[
2
π
(
f
0
t
+
α
2
t
2
)
t
+
θ
0
]
\textup{FMCW}=Ae^{j[2\pi (f_0t+\frac{\alpha}{2}t^2)t+\theta_0]}
FMCW=Aej[2π(f0t+2αt2)t+θ0]其中
f
0
f_0
f0为初始频率,
α
\alpha
α为斜率。设往返ToF为
τ
\tau
τ,则接收到的反射信号为
Reflection
=
e
−
j
{
2
π
[
f
0
(
t
−
τ
)
+
α
2
(
t
−
τ
)
2
]
t
+
θ
0
}
\textup{Reflection}=e^{-j\{2\pi [f_0(t-\tau)+\frac{\alpha}{2}(t-\tau)^2]t+\theta_0\}}
Reflection=e−j{2π[f0(t−τ)+2α(t−τ)2]t+θ0}
注意反射波与入射波是反相的。
使用混频器,通过将反射信号乘以发射信号的复共轭,与发射信号进行比较,得到的信号称为拍频信号:
BeatFreqSignal
≈
e
j
2
π
(
α
t
τ
+
f
0
τ
)
\textup{BeatFreqSignal}\approx e^{j2\pi(\alpha t\tau+f_0\tau)}
BeatFreqSignal≈ej2π(αtτ+f0τ)其中高阶项
π
α
τ
2
\pi\alpha\tau^2
πατ2被忽略。
可见拍频信号的瞬时相位等于TX和RX的瞬时相位之差。将拍频信号在时域进行标准快速傅里叶变换后,可在与拍频
α
τ
\alpha\tau
ατ对应的频率区间得到峰值功率,相应的相位为
2
π
f
0
τ
2\pi f_0\tau
2πf0τ。
到达角和运动引入失真:使用傅里叶变换提取距离信息
ρ
\rho
ρ后,会比较来自多个天线的拍频信号以估计到达角(AoA)
ϕ
\phi
ϕ。这一步比较的实际上是相位差
Δ
θ
i
j
=
2
π
f
0
Δ
τ
i
j
\Delta \theta_{ij}=2\pi f_0\Delta \tau_{ij}
Δθij=2πf0Δτij而非ToF之差
Δ
τ
i
j
\Delta \tau_{ij}
Δτij。
线性阵列中,相位差
Δ
θ
i
j
=
2
π
f
0
Δ
τ
i
j
=
2
π
f
0
(
τ
j
−
τ
i
)
=
2
π
l
sin
ϕ
λ
(
j
−
i
)
\Delta \theta_{ij}=2\pi f_0\Delta \tau_{ij}=2\pi f_0(\tau_j-\tau_i)=2\pi\frac{l\sin\phi}{\lambda}(j-i)
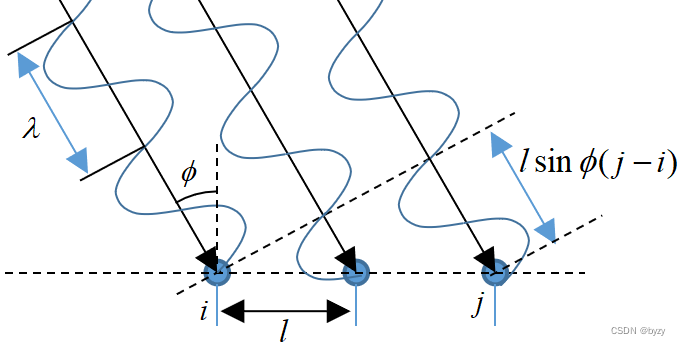
Δθij=2πf0Δτij=2πf0(τj−τi)=2πλlsinϕ(j−i)其中
l
l
l为天线间距,
λ
\lambda
λ为波长。
上式可用图表示如下:
对于MIMO雷达,若发射间隔为
δ
t
i
j
\delta t_{ij}
δtij,则上式变为
Δ
θ
i
j
′
=
2
π
l
sin
ϕ
λ
(
j
−
i
)
+
2
π
f
0
δ
t
i
j
2
v
c
\Delta \theta'_{ij}=2\pi\frac{l\sin\phi}{\lambda}(j-i)+2\pi f_0\delta t_{ij}\frac{2v}{c}
Δθij′=2πλlsinϕ(j−i)+2πf0δtijc2v可见,对于运动物体,由于
f
0
f_0
f0很大,即使速度很小,也会剧烈改变相位差,从而使距离-水平角热图失真。
附录F: 运动引入失真的补偿算法
co-located的虚拟天线对被相邻的物理TX模拟。co-located虚拟天线对的时间间隔为一个chirp的时间间隔
Δ
T
\Delta T
ΔT,且不存在与AoA相关的相位差。这样,上式进一步变为
Δ
θ
i
j
†
=
2
π
f
0
δ
t
i
i
′
2
v
c
\Delta \theta^\dagger_{ij}=2\pi f_0\delta t_{ii'}\frac{2v}{c}
Δθij†=2πf0δtii′c2v 通过在每个距离区间内测量每对co-located天线之间的相位差,并取所有co-located天线对的测量值中位数作为最终的运动引入相位变化的估计。最后使用发射间隔
δ
t
\delta t
δt来放缩估计的运动引入相位变化,并通过对每个虚拟天线乘以相反相位的相量来补偿。
最后使用不重叠的虚拟天线提取反射角度信息。虽然多数情况下该算法的效果较好,但对于相对高速情况仍存在误差。
附录G: 多普勒预处理算法
由于一帧雷达数据包含
K
K
K个chirp,因此可使用同一虚拟天线在时间上的相位差(
Δ
θ
†
\Delta\theta^\dagger
Δθ†),类似前面的方法(上式)来提取多普勒信息,从而得到速度:
v
=
c
4
π
f
0
⋅
N
T
Δ
θ
†
=
λ
4
π
N
T
Δ
θ
†
v=\frac{c}{4\pi f_0\cdot NT}\Delta\theta^\dagger=\frac{\lambda}{4\pi NT}\Delta\theta^\dagger
v=4πf0⋅NTcΔθ†=4πNTλΔθ†其中
T
T
T为相邻chirp的时间间隔,
N
N
N为TX的数量。
标准算法是沿chirps使用另一个快速傅里叶变换,得到3D距离-水平角-多普勒(RAD)张量。不同速度的物体被分组到不同的多普勒区间。但对于级联雷达来说,每根天线的两个chirp之间的时间很长,会导致速度域的混叠,即不同速度范围的物体会落入同一个速度区间中。
为解决混叠问题,可以使用相邻天线的发射时间间隔,但相邻天线的chirp并不是co-located的,因此除了运动引入的相位变化外还有与AoA相关的相位差。但之前的工作中对两个相位差进行了解耦,可对AoA相关的相位差进行补偿。
具体来说,本文分别处理每个TX的RA热图,共可产生
N
⋅
K
N\cdot K
N⋅K个RA热图。通过乘以TX阵列方向向量的复共轭补偿AoA相关的相位差后,在
N
⋅
K
N\cdot K
N⋅K的维度上进行快速傅里叶变换,得到RAD热图,其角度分辨率与低分辨率RA热图相同,但速度分辨率以及不产生混叠的最大速度均很高。
虽然由于不完美的AoA相位补偿,仍然存在速度混叠,每个物体的主要速度通常对应多普勒维度的最高功率区间。因此本文通过对每一个RA网格,沿多普勒维度进行argmax操作,得到2D的RA-多普勒索引特征图。这样混叠部分由于功率较低而被忽略,且3D RAD张量的稀疏性得到减轻,使用小型神经网络能更容易地学习。该RA-多普勒索引特征图被作为Radatron单一TX输入的第二通道。






![[附源码]JAVA毕业设计框架的电脑测评系统(系统+LW)](https://img-blog.csdnimg.cn/28d7120757514faab44a7c785fac3ffe.png)

