智能优化算法：法医调查优化算法

摘要：法医调查优化算法( Forensic-based investigation algorithm, FBI), 是由 Jui-Sheng Chou 等于2020 年提出的一种群体智能优化算法。其灵感来源于警官调查嫌疑人的过程。

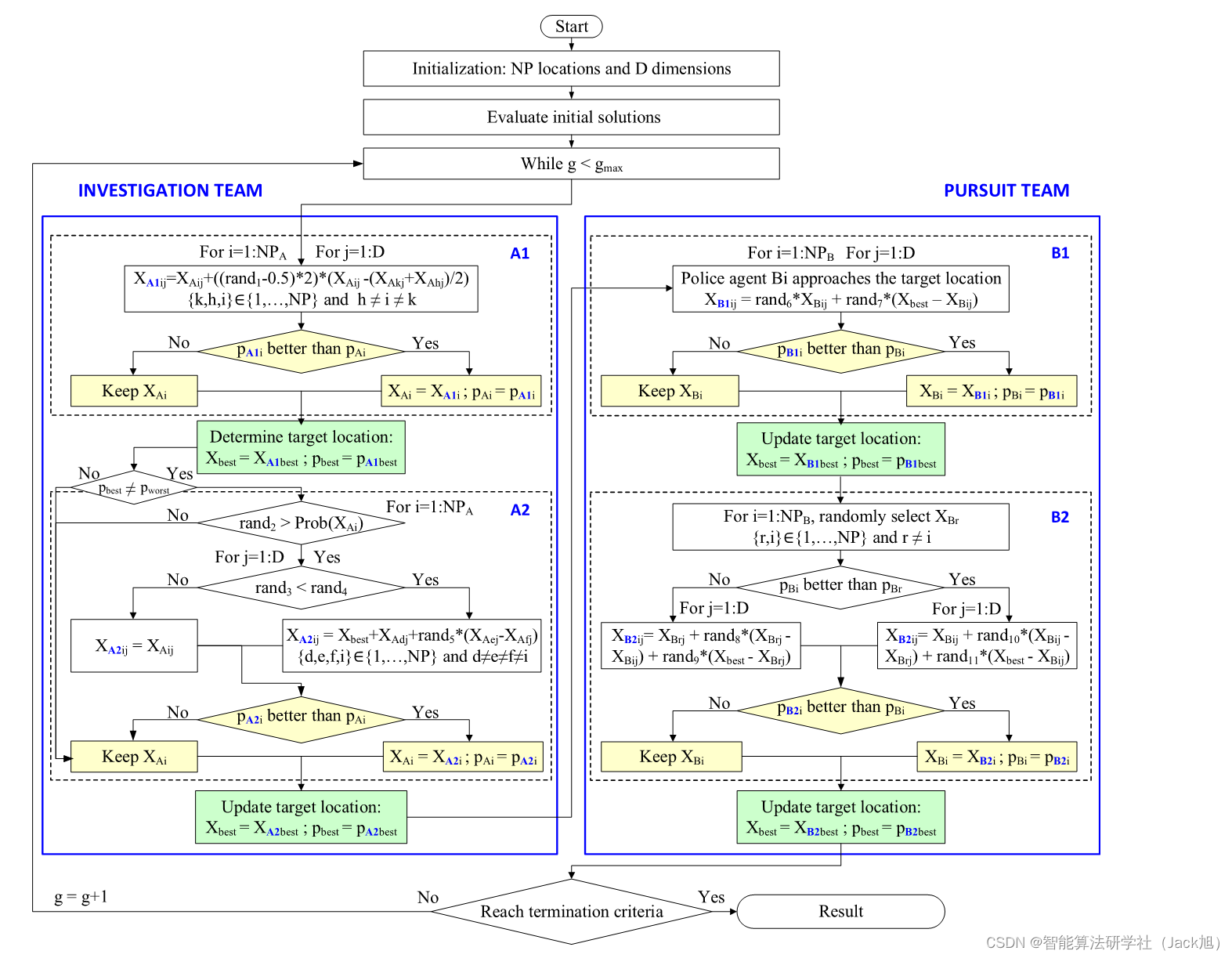
1.法医调查优化算法

警察的大规模案件调查通常包括五个步骤，其中步骤2、3和4可视为一个循环过程。

立案：对这起事件的调查从最先到达犯罪现场的警察发现的信息开始。这些信息构成了调查小组成员的主要出发点，他们从遵循几个标准程序开始，以获得可能发生的事情的第一印象。小组成员调查犯罪现场、受害者、可能的嫌疑人及其背景信息；小组找到证人并询问证人。
分析调查结果：通过在团队简报中共享信息，团队成员试图获得所有可用信息的概述。在第二步中，团队评估信息，并尝试将信息与他们对案件已有的印象联系起来，以评估可能的嫌疑人。
调查方向：在调查的第三步中，团队成员根据对调查结果的分析，做出几种猜想(包括犯罪场景、犯罪动机和调查路线)。团队再次评估调查结果，得出新的方向，或确认、更改或终止现有的调查方向。
行动：在确定了调查路线和优先顺序后，警察团队就要采取的进一步行动做出决定。这一步骤与关于优先事项的决策密切相关，通常首先追求最有希望的研究方向。所采取的行动再次提供了新的信息。一旦获得该信息，调查小组将根据现有信息解释其含义或含义。对新发现的分析可能会导致调查和行动方向的调整。
起诉：在做出起诉决定之前，一旦确定了一名严重嫌疑人，诉讼就结束了。

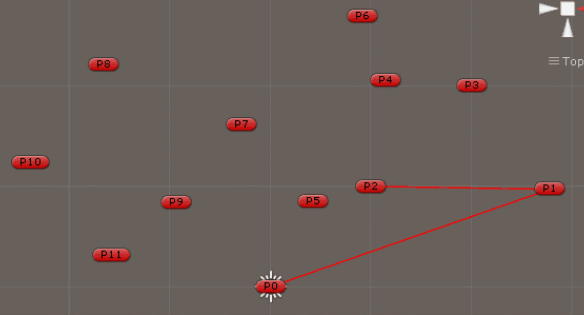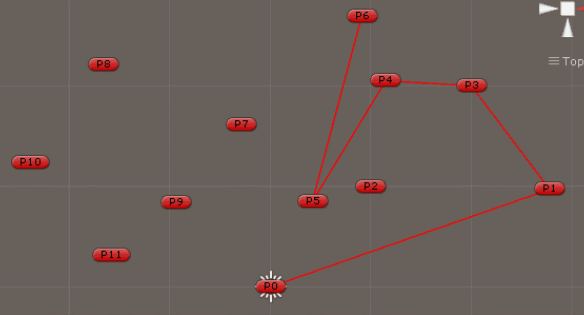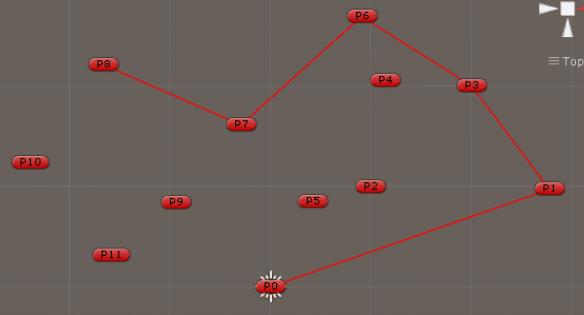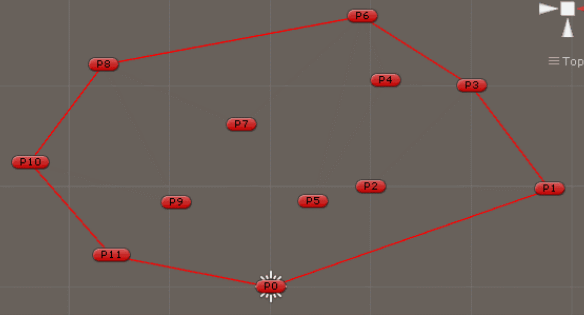
1.1 分析调查A1

该小组评估了信息，并初步确定了可能的可疑地点。在其他调查结果的背 景下，对嫌疑人的每个可能位置进行调查。首先，根据 $X_{{\mathrm{A}}_{\mathrm{i}}}$ 和其他可疑位置的相关信息，推断出 ${\mathrm{X}}_{{\mathrm{A}}_{\mathrm{i}}}$ 的一个新
$${\mathrm{X}}_{\mathrm{A}{1}_{\mathrm{i}\mathrm{j}}}={\mathrm{X}}_{{\mathrm{A}}_{\mathrm{i}\mathrm{j}}}+{\left((\mathrm{rand}-0.5{)}^{\ast }2\right)}^{\ast }\left(\sum _{\mathrm{a}=1}^{{\mathrm{a}}_1}{\mathrm{X}}_{{\mathrm{A}}_{\mathrm{a}\mathrm{j}}}\right)/{\mathrm{a}}_1\text{\hspace{1em}(1)}$$
其中， $\mathrm{j}=1,2,\cdots ,\mathrm{D};\mathrm{D}$ 为问题的维数； $\left((\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}-0.5{)}^{\ast }2\right)$ 表示一个 $[-1,1]$ 的随机数； rand表示一个 $[0,1]$ 的随机数； a 1 ∈ { 1 , 2 , ⋯   , n − 1 } \mathrm{a}_1 \in\{1,2, \cdots, \mathrm{n}-1\} a1​∈{1,2,⋯,n−1} 表示影响 ${\mathrm{X}}_{{\mathrm{A}}_{\mathrm{i}\mathrm{j}}}$ 移动个体数量; $\mathrm{a}=1,2,\cdots ,{\mathrm{a}}_1$ 。实验表明， $\mathrm{a}1=2$ 能够在较短的计算时间内产生最佳结果。因此，新的可疑位置 ${\mathrm{X}}_{\mathrm{A}{1}_{\mathrm{i}}}$ 如式(2)计算； ${\mathrm{p}}_{{\mathrm{A}}_{\mathrm{i}}}$ 定义为嫌疑人在 ${\mathrm{X}}_{{\mathrm{A}}_{\mathrm{i}}}$ 位置的概率(目标值)，这意味着 ${\mathrm{p}}_{{\mathrm{A}}_{\mathrm{i}}}$ 是 ${\mathrm{X}}_{{\mathrm{A}}_{\mathrm{i}}}$ 位置的目标值(即 ${\mathrm{p}}_{{\mathrm{A}}_{\mathrm{i}}}={\mathrm{f}}_{\text{objective }}\left({\mathrm{A}}_{\mathrm{i}}\right)$ )。 将保留嫌疑人存在概率 更大(目标值)的位置，而放弃另一个位置。
$${\mathrm{X}}_{\mathrm{A}{1}_{\mathrm{i}\mathrm{j}}}={\mathrm{X}}_{{\mathrm{A}}_{\mathrm{i}\mathrm{j}}}+{\left({\left({\mathrm{rand}}_1-0.5\right)}^{\ast }2\right)}^{\ast }\left({\mathrm{X}}_{{\mathrm{A}}_{\mathrm{i}\mathrm{j}}}-\left({\mathrm{X}}_{{\mathrm{A}}_{\mathrm{k}\mathrm{j}}}+{\mathrm{X}}_{{\mathrm{A}}_{\mathrm{h}\mathrm{j}}}\right)/2\right)\text{\hspace{1em}(2)}$$
其中， $\mathrm{k}、\mathrm{h}$ 和 $\mathrm{i}$ 是三个可疑位置: { k , h , i } ∈ { 1 , 2 , ⋯   , N P } ， k \{\mathrm{k}, \mathrm{h}, \mathrm{i}\} \in\{1,2, \cdots, \mathrm{NP}\} ， \mathrm{k} {k,h,i}∈{1,2,⋯,NP}，k 和 $\mathrm{h}$ 随机选择; $\mathrm{j}=1,2,\cdots ,\mathrm{D};\mathrm{N}\mathrm{P}$ 是 可疑位置的数量； $\mathrm{D}$ 为问题的维数； $\left({\left({\mathrm{rand}}_1-0.5\right)}^{\ast }2\right)$ 表示一个 $[-1,1]$ 的随机数； ${\mathrm{rand}}_1$ 表示一个 $[0,1]$ 的 随机数。

1.2 分析调查A2

调查人员将每个可疑位置的概率与其他位置的概率进行比较，以确定应进一步 调查的最可能的可疑位置。当优化是一个最小化问题时， ${\mathrm{p}}_{\mathrm{w}\mathrm{o}\mathrm{r}\mathrm{s}\mathrm{t}}$ 是最低概率(最差目标值)， ${\mathrm{p}}_{\text{best }}$ 是最高概率(最 佳目标值)， ${\mathrm{X}}_{\text{best }}$ 是最佳位置。可以理解的是，虽然 ${\mathrm{p}}_{\text{worst }}$ 与 ${\mathrm{p}}_{\text{best }}$ 不同，但任何概率较低的位置都可能会被放 弃，转而选择另一个概率较高的位置。使用式(3)评价每个位置的概率 $\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left({\mathrm{X}}_{{\mathrm{A}}_{\mathrm{i}}}\right)，\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left({\mathrm{X}}_{{\mathrm{A}}_{\mathrm{i}}}\right)$ 的高值对应 于该位置的高概率。
$$\mathrm{Prob}\left({\mathrm{X}}_{{\mathrm{A}}_{\mathrm{i}}}\right)=\left({\mathrm{p}}_{\text{worst }}-{\mathrm{p}}_{{\mathrm{A}}_{\mathrm{i}}}\right)/\left({\mathrm{p}}_{\text{worst }}-{\mathrm{p}}_{\text{best }}\right)\text{\hspace{1em}(3)}$$
搜索位置的更新受其他可疑位置的方向影响。然而，并非所有方向都改变了；更改更新位置中随机选择的方 向，以增加搜索区域的多样性。在这一步中， ${\mathrm{X}}_{{\mathrm{A}}_{\mathrm{i}}}$ 的移动只受最佳个体和其他随机个体的影响。步骤A2类似于 步骤 $\mathrm{A}1$ ， 式(4)给出了移动的一般公式。
$${\mathbf{X}}_{\mathrm{A}{2}_{\mathrm{i}}}={\mathbf{X}}_{\text{best }}+\sum _{\mathrm{b}=1}^{\mathrm{a}2}{\alpha }_{\mathrm{b}}{}^{\ast }{\mathbf{X}}_{{\mathrm{A}}_{\mathrm{b}\mathrm{j}}}\text{\hspace{1em}(4)}$$
其中， ${\mathrm{X}}_{\text{best }}$ 为最佳位置； ${\mathrm{a}}_2$ 是影响 ${\mathrm{X}}_{\mathrm{A}{2}_{\mathrm{i}}}$ 移动的个体数： a 2 ∈ { 1 , 2 , ⋯   , n − 1 } ; b = 1 , 2 , ⋯   , a 2 \mathrm{a}_2 \in\{1,2, \cdots, \mathrm{n}-1\} ; \mathrm{b}=1,2, \cdots, \mathrm{a}_2 a2​∈{1,2,⋯,n−1};b=1,2,⋯,a2​ ； ${\alpha }_{\mathrm{b}}\left({\alpha }_{\mathrm{b}}\in [-1,1]\right)$ 是其他个体移动的有效系数。数值实验得出 ${\mathrm{a}}_2=3$ 。因此，使用式(5)生成新的可疑位置
$${\mathrm{X}}_{\mathrm{A}{2}_{\mathrm{i}\mathrm{j}}}={\mathrm{X}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}+{\mathrm{X}}_{{\mathrm{A}}_{\mathrm{d}\mathrm{j}}}+{\mathrm{rand}}_5{}^{\ast }\left({\mathrm{X}}_{{\mathrm{A}}_{\mathrm{e}\mathrm{j}}}-{\mathrm{X}}_{{\mathrm{A}}_{\mathrm{f}\mathrm{j}}}\right)\text{\hspace{1em}(5)}$$
其中， ${\mathrm{X}}_{\text{best 是在步骤 }}\mathrm{A}$ 中更新的最佳位置， ${\mathrm{rand}}_5$ 是 $[0,1]$ 范围内的随机数； $\mathrm{d},\mathrm{e},\mathrm{f},\mathrm{i}$ 为四个可疑位置： { d , e , f , i } ∈ { 1 , 2 , ⋯   , N P } \{\mathrm{d}, \mathrm{e}, \mathrm{f}, \mathrm{i}\} \in\{1,2, \cdots, \mathrm{NP}\} {d,e,f,i}∈{1,2,⋯,NP} ， d, e和f随机选择； $\mathrm{j}=1,2,\cdots ,\mathrm{D}$ 。

1.3 行动B1

该部分对应着“行动”步骤。在收到调查小组关于最佳位置的报告后，追捕小组中的所有特工必须以协调的方式 接近目标，以逮捕嫌疑人。根据式(6)，每个代理 $B_{\mathrm{i}}$ 接近具有最佳概率(目标值)的位置。如果新接近的位置产生 的概率(目标值)比旧位置的概率 $\left({\mathrm{p}}_{\mathrm{B}\mathrm{i}}\right)$ 更好，则更新该位置。
$${\mathrm{X}}_{\mathrm{B}{1}_{\mathrm{i}\mathrm{j}}}={\mathrm{rand}}_6{}^{\ast }{\mathrm{X}}_{{\mathrm{B}}_{\mathrm{i}\mathrm{j}}}+{\mathrm{rand}}_7{}^{\ast }\left({\mathrm{X}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}-{\mathrm{X}}_{{\mathrm{B}}_{\mathrm{i}\mathrm{j}}}\right)\text{\hspace{1em}(6)}$$
其中， $X_{\text{best }}$ 是调查小组提供的最佳位置； ${\mathrm{rand}}_6$ 和 ${\mathrm{rand}}_7$ 为两个 $[0,1]$ 范围内的随机数； $\mathrm{j}=1,2,\cdots ,\mathrm{D}$ 。

1.4 行动B2

该部分扩展了“行动”步骤。无论何时采取任何行动，警察都会向总部报告新地点的概率(目标值)。总部立即更新位置，并命令追捕小组接 近该位置。此时，每个代理 $B_i$ 与所有其他代理进行密切协调；代理 $B_i$ 向最佳位置移动，代理 $B_i$ 受到其他团队成员(代理 $B_r$ ，概率为 $p_{B_r})$ 的 (目标值)时，将更新该位置。
$$\begin{array}{cc}{\mathrm{X}}_{\mathrm{B}{2}_{\mathrm{i}\mathrm{j}}}={\mathrm{X}}_{{\mathrm{B}}_{\mathrm{r}\mathrm{j}}}+{\mathrm{rand}}_8{}^{\ast }\left({\mathrm{X}}_{{\mathrm{B}}_{\mathrm{r}\mathrm{j}}}-{\mathrm{X}}_{{\mathrm{B}}_{\mathrm{i}\mathrm{j}}}\right)+{\mathrm{rand}}_9{}^{\ast }\left({\mathrm{X}}_{\text{best }}-{\mathrm{X}}_{{\mathrm{B}}_{\mathrm{r}\mathrm{j}}}\right)& (7)\\ {\mathrm{X}}_{\mathrm{B}{2}_{\mathrm{i}\mathrm{j}}}={\mathrm{X}}_{{\mathrm{B}}_{\mathrm{i}\mathrm{j}}}+{\mathrm{rand}}_{10}{}^{\ast }\left({\mathrm{X}}_{{\mathrm{B}}_{\mathrm{i}\mathrm{j}}}-{\mathrm{X}}_{{\mathrm{B}}_{\mathrm{r}\mathrm{j}}}\right)+{\mathrm{rand}}_{11}{}^{\ast }\left({\mathrm{X}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}-{\mathrm{X}}_{{\mathrm{B}}_{\mathrm{i}\mathrm{j}}}\right)& (8)\end{array}$$
其中， ${\mathrm{X}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}$ 是步骤B1中提供的最佳位置， ${\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}}_8,{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}}_9,{\mathrm{rand}}_{10}$ 和 ${\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}}_{11}$ 是 $[0,1]$ 范围内的随机数； $\mathrm{r}$ 和㧑两个警察代理： { r , i } ∈ \{\mathrm{r}, \mathrm{i}\} \in {r,i}∈ { 1 , 2 , ⋯   , N P } \{1,2, \cdots, \mathrm{NP}\} {1,2,⋯,NP} ，且r随机选择; $\mathrm{j}=1,2,\cdots ,\mathrm{D}$ 。

3.实验结果

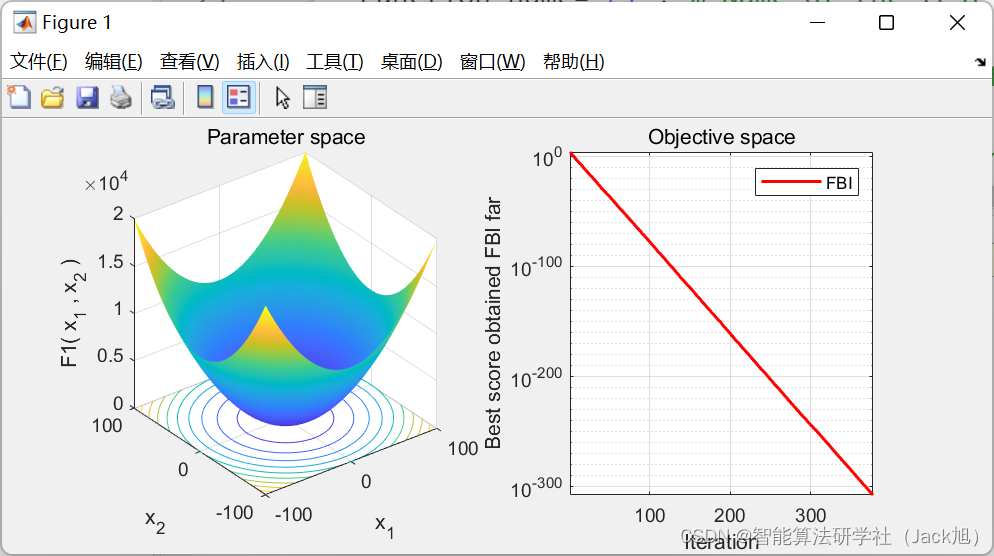
4.参考文献

[1] Jui-Sheng Chou, Ngoc-Mai Nguyen, FBI inspired meta-optimization, Applied Soft Computing, Volume 93, 2020, 106339, ISSN 1568-4946

5.Matlab代码

6.python代码