泰勒公式

用柯西定理证明
拉格朗日余项

麦克劳林展开式:

皮亚诺余项的泰勒公式:
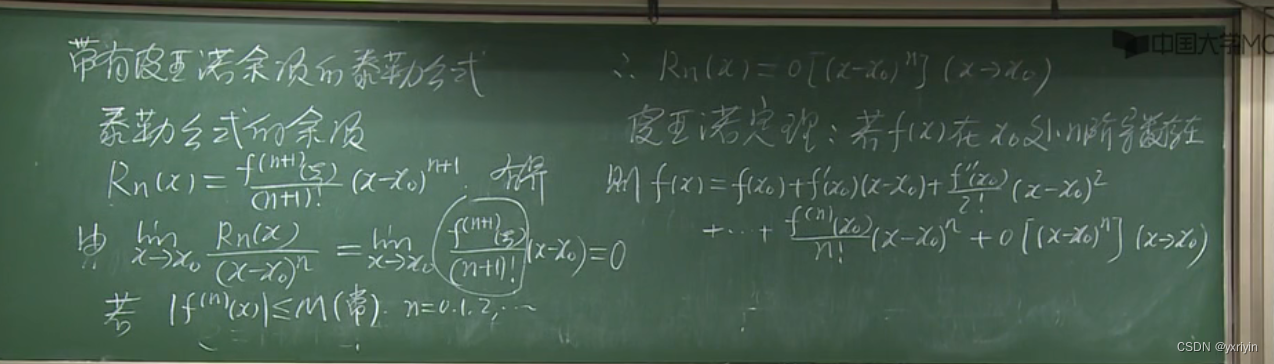
弧长的微分

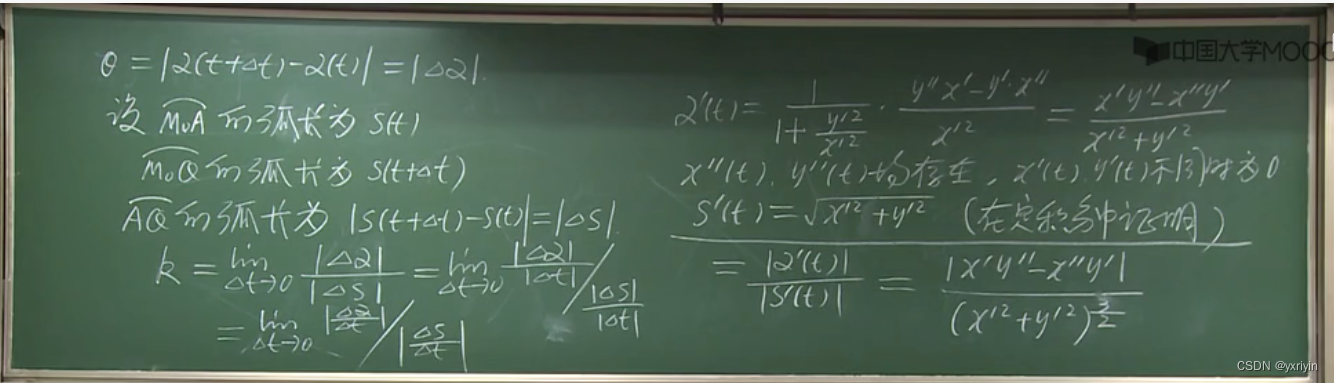
注意s'(t)需要在后面证明(定积分的知识)
不定积分:

注意,不同的积分方法经常会得到不同的结果,但它们一定只相差一个常数
定积分:


可积分的充分条件:

积分中值定理:

微积分基本定理:

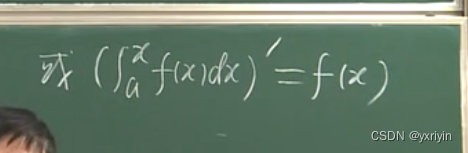
注意积分变量和上限变量是不一样的,但都写成x方便。
积分变量可以随便换。
牛顿-莱布尼兹公式

一般变限积分求导
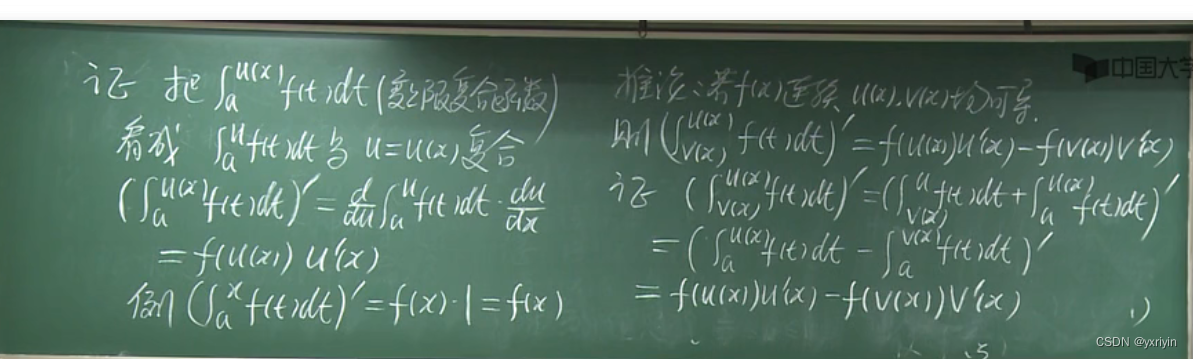
曲线弧长:
 在此证明
在此证明

圆的周长公式:

弧长微分公式:

圆台侧面积问题:

注意,在做近似的时候,需要保证误差必须是变量的高阶无穷小
也就是y = f'(x)dx + o(
x)
直观的理解是,考虑一个球的体积,相对于体积而言,圆台和圆柱的差距很小,
所以微元法看成梯形还是矩形并不影响大局。当然端点例外,但因为只有那一个点有这个问题。
但是如果是表面积,圆台和圆柱的差距就不可忽略了。
第一类广义积分:

第二类广义积分:

收敛级数的性质:


柯西-阿玛达公式:

收敛区间的收敛幂级数逐项可导,逐项可积,而且收敛区间不变


求幂级数的方法:

函数展开成幂级数:




求积分的新方法:

唯一性定理:

看一个例子:
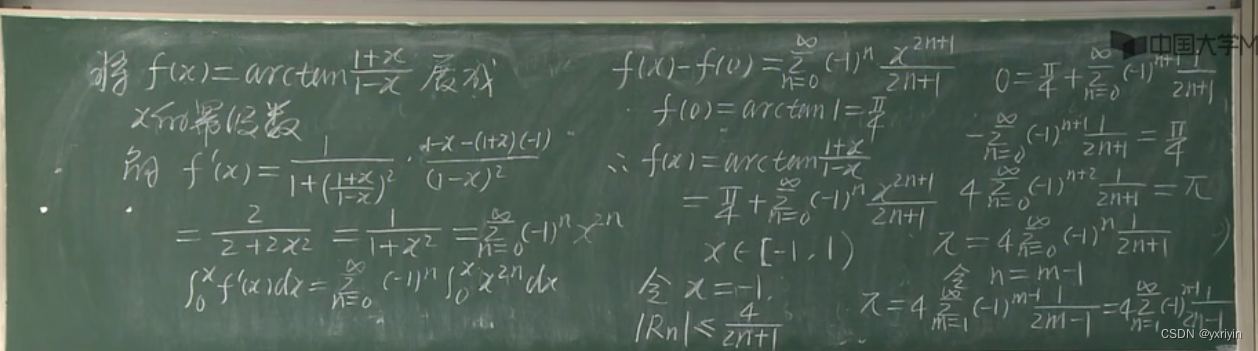
能展开幂级数之后,求导和积分都好做。
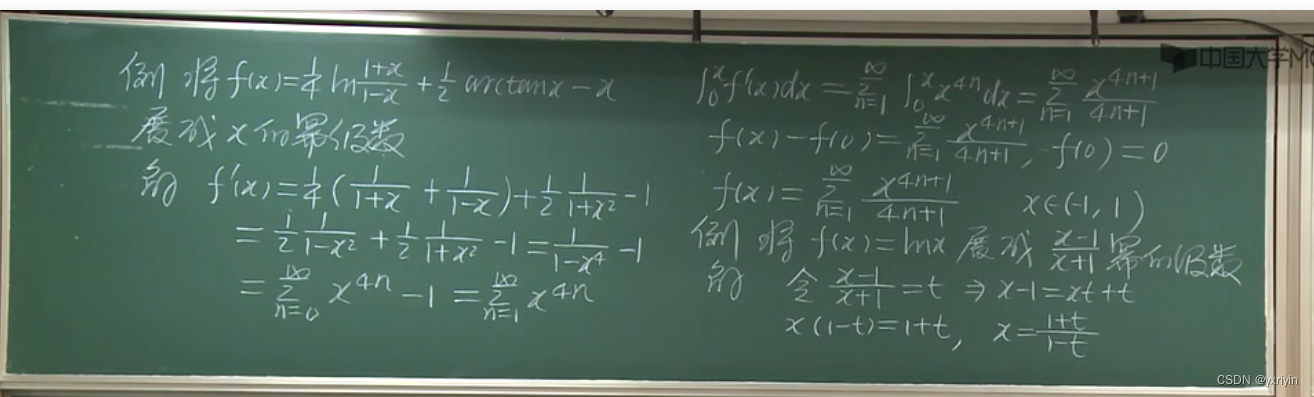
![[附源码]JAVA毕业设计抗击新冠疫情专题宣传网站(系统+LW)](https://img-blog.csdnimg.cn/8626ba7453da4f43829805da6393379f.png)


![[附源码]Python计算机毕业设计Django楼盘销售管理系统](https://img-blog.csdnimg.cn/4cb2eca455744795b9250235afd1b553.png)