Problem - 1627C - Codeforces

题意：

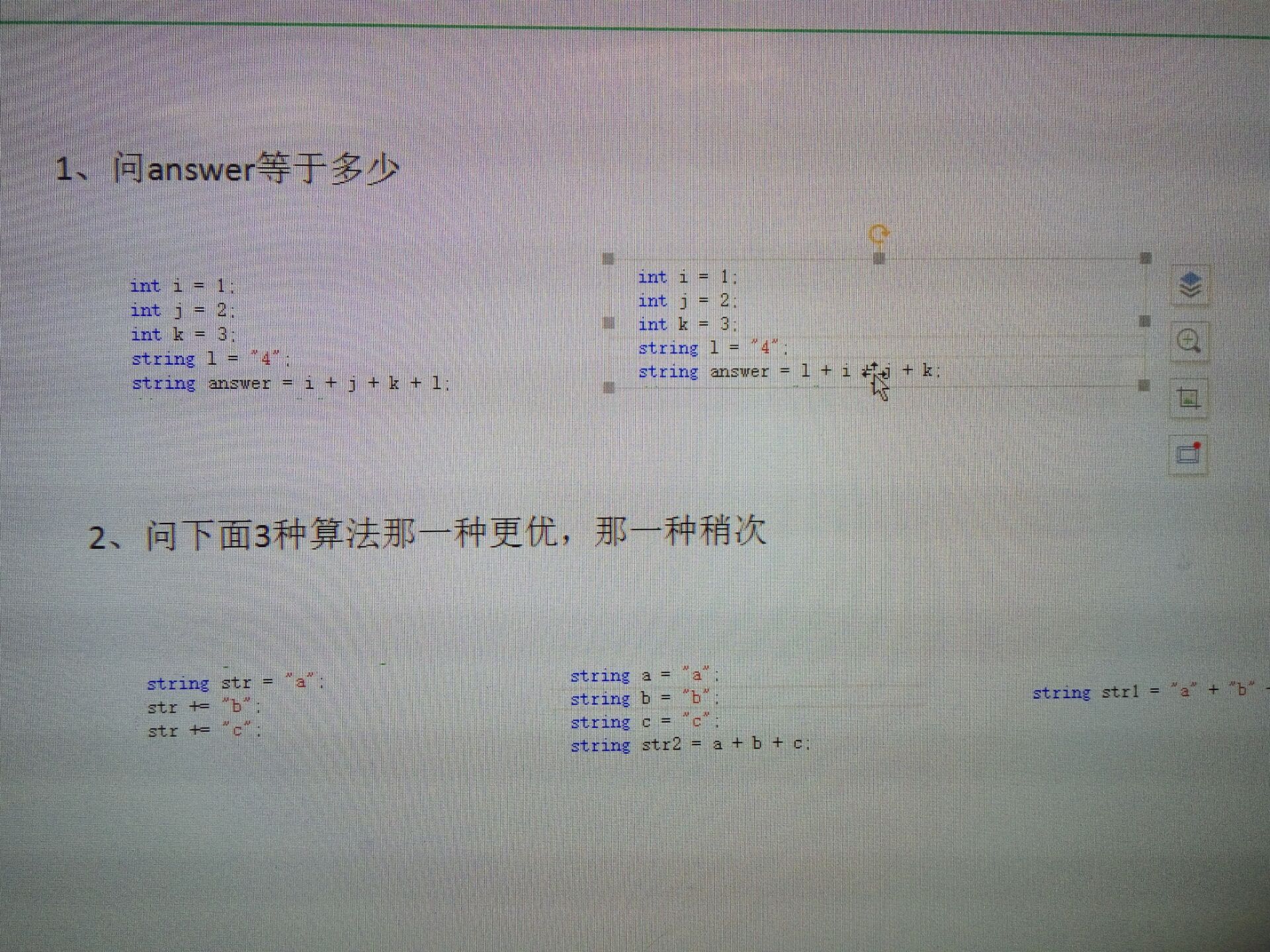
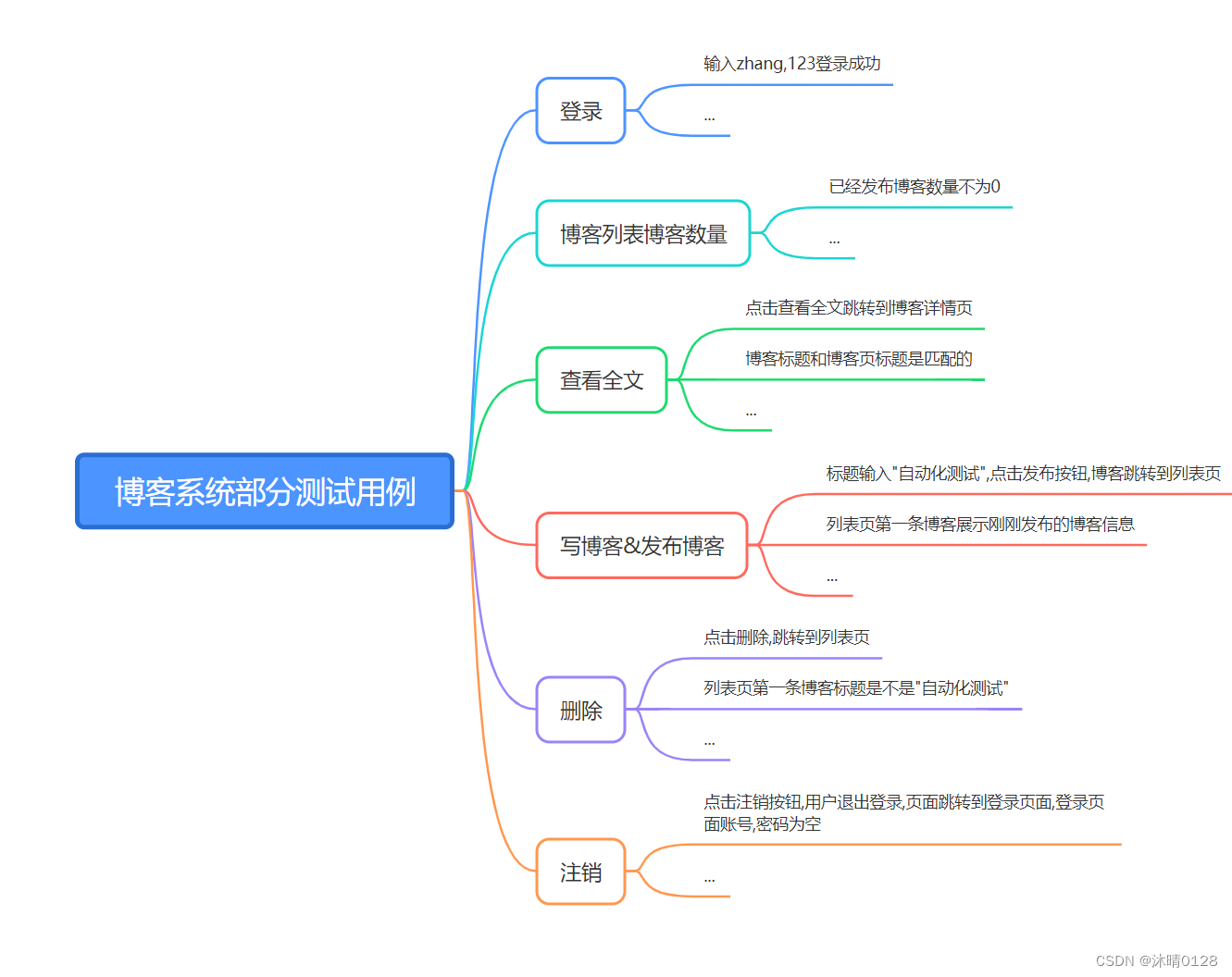
给定一棵树的形态，让你给这棵树的边赋值，使得每对相邻的边的边权和都是质数

思路：

一开始模拟了一下样例，Sample3告诉我们如果有三条边相邻就是无解（可以猜的结论）

然后不知道该怎么具体赋值，不知道该怎么特殊化边权

事实上，只需要2，3，2，3这样子赋值即可

感觉2000分以下的构造

如果出的简单一点，那就是手推样例，直接模仿样例给的构造，或者直接最特殊的情况，这种最特殊的情况就算全部猜一遍也能猜出来

难的我也不懂，还没写过难的构造题

Code：

#include <bits/stdc++.h>

#define int long long

using namespace std;

const int mxn=1e5+10;
const int mxe=1e5+10;

struct ty{
    int to,next,id;
}edge[mxe<<2];

int N;
int u,v,tot=0;

int a[mxn];
int in[mxn],head[mxn];

void G_init(){
    tot=0;
    for(int i=0;i<=N;i++){
        head[i]=-1;
        in[i]=0;
    }
}
void add(int u,int v,int id){
    edge[tot].id=id;
    edge[tot].to=v;
    edge[tot].next=head[u];
    head[u]=tot++;
}
void dfs(int u,int fa,int c){
    for(int i=head[u];~i;i=edge[i].next){
        if(edge[i].to==fa) continue;
        a[edge[i].id]=c;
        dfs(edge[i].to,u,c^1);
    }
}
void solve(){
    cin>>N;
    G_init();
    for(int i=1;i<=N-1;i++){
        cin>>u>>v;
        add(u,v,i);
        add(v,u,i);
        in[u]++;
        in[v]++;
    }
    int mi=1e9,ansi=1;
    for(int i=1;i<=N;i++){
        if(in[i]>2){
            cout<<-1<<'\n';
            return;
        }
        if(mi>in[i]){
            mi=in[i];
            ansi=i;
        }
    }
    dfs(ansi,0,0);
    for(int i=1;i<=N-1;i++) cout<<a[i]+2<<" \n"[i==N-1];
}
signed main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int __=1;cin>>__;
    while(__--)solve();return 0;
}