目录
最小栈
栈的压入与弹出
逆波兰表达式
最小栈
155. 最小栈 - 力扣(Leetcode)
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack()初始化堆栈对象。void push(int val)将元素val推入堆栈。void pop()删除堆栈顶部的元素。int top()获取堆栈顶部的元素。int getMin()获取堆栈中的最小元素。
刚刚开始,我认为可以写一个栈存放数据,一个int保存最小值,但是如果最小值在栈中呗pop时,我们就找不到之前的最小值了

设计双栈解决该问题
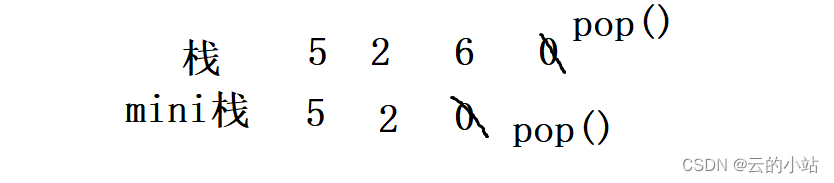
mini栈的栈顶就是最小值存放栈数据中的。 当我们栈pop时只需要比较是否与mini.top()是否相等,相等mini.pop(),否则不动

如果多次压入多个0(最小值)我们也需要在mini栈压入0。否者在栈pop最小值时会把mini唯一最小值删除,但是pop的最小值是多个的,数据会出错。

栈.pop()。是把0删除,这次删除也会把mini栈0删除,删除后mini.top=2,而实际栈最小数据==0

所以我们需要在压入数据如果与mini.top相同或小于,mini.top也压入数据。
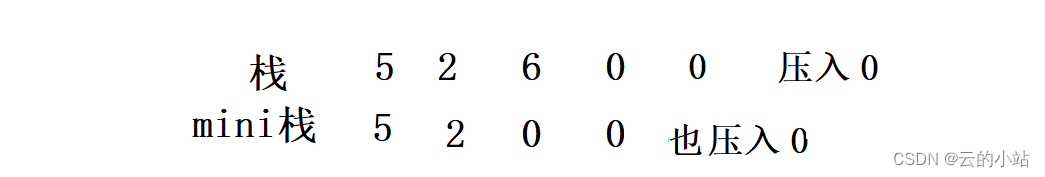
这样如果我们删除栈.pop(),此刻最小值依旧是0,而mini.top()也为0。

假设极端情况:最小值非常非常非常多,最小值1有100w个
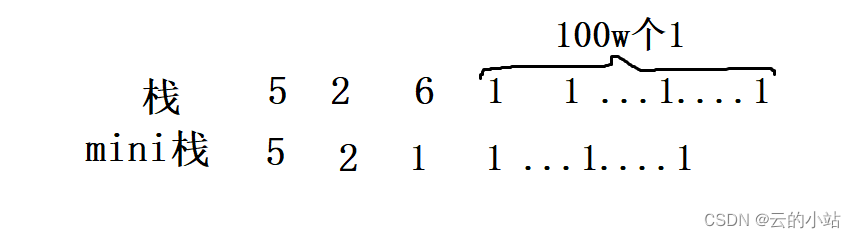
此时最小栈也要存放100w个1,极大的浪费了空间,所以我们使用计数器(一个结构体,里面保存最小值,以及最小值数量)
struct Intcount
{
Intcount(int x = 0)
:_val(x)
, count(1)
{}
int _val;
int count;
};使用计数器代替了stack<int>-->stack<Intcount>
实现代码:
struct Intcount
{
Intcount(int x = 0)
:_val(x)
, count(1)
{}
int _val;
int count;
};
class MinStack {
private:
std::stack<Intcount> _minst;
std::stack<int> st;
public:
void push(int val) {
if (_minst.size() == 0)
{
_minst.push(val);
st.push(val);
}
else
{
st.push(val);
if (st.top() == _minst.top()._val)
{
++_minst.top().count;
}
else if(st.top() < _minst.top()._val)
{
_minst.push(val);
}
}
}
void pop() {
if (st.top() == _minst.top()._val)
{
--_minst.top().count;
if (_minst.top().count == 0)
{
_minst.pop();
}
}
st.pop();
}
int top() {
return st.top();
}
int getMin() {
return _minst.top()._val;
}
};栈的压入与弹出
栈的压入、弹出序列_牛客题霸_牛客网 (nowcoder.com)
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹出序列。
1. 0<=pushV.length == popV.length <=1000
2. -1000<=pushV[i]<=1000
3. pushV 的所有数字均不相同
一句话,判断出栈顺序是否合法。
开辟一个栈
将popV与pushV的数据拿出来,将pushV的数据加载到栈中。
那栈顶的数据与popV的数据比较,如果相等就pop栈顶数据并且popV的下标++,无论相等不相等都要一直载入pushV数据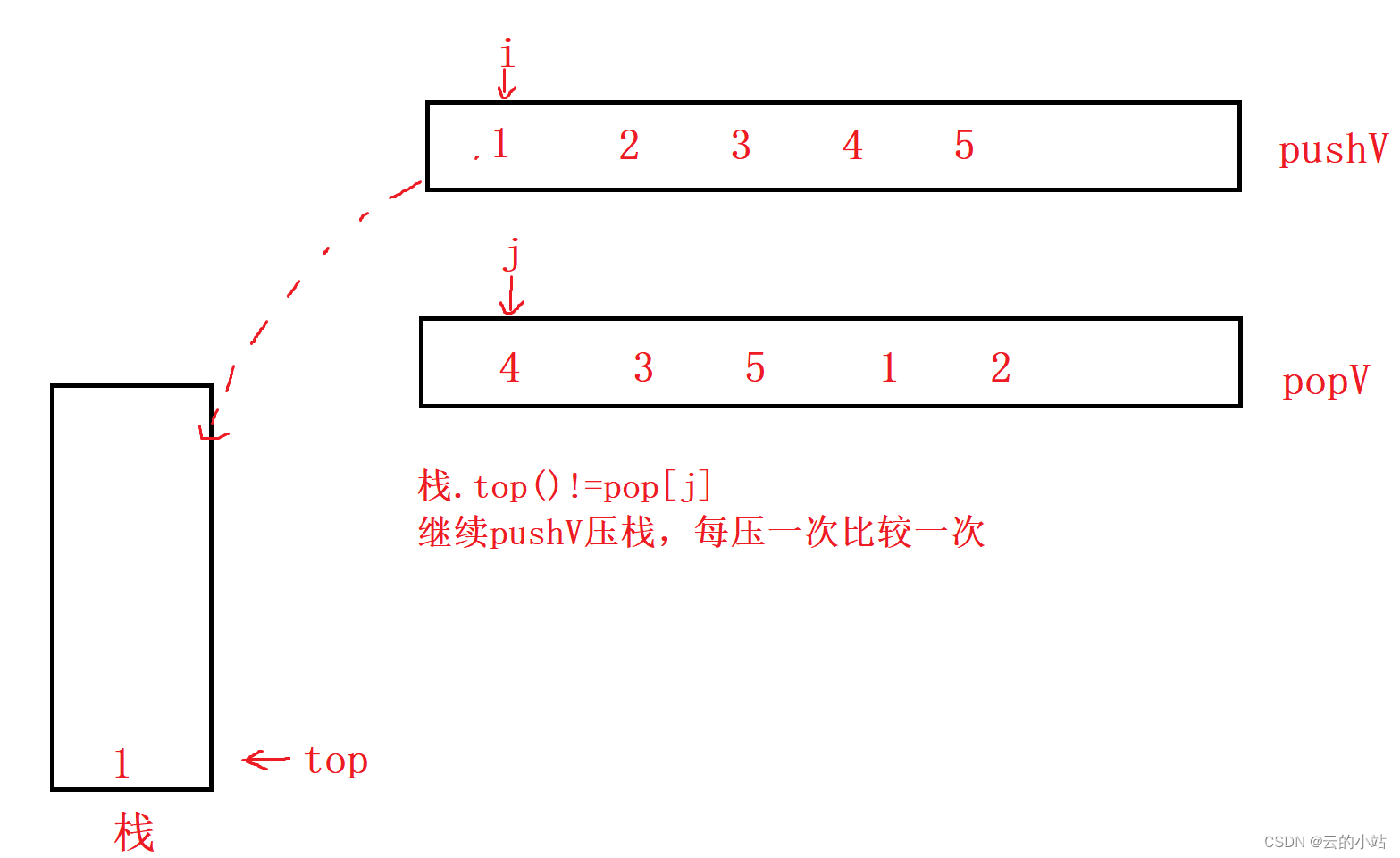
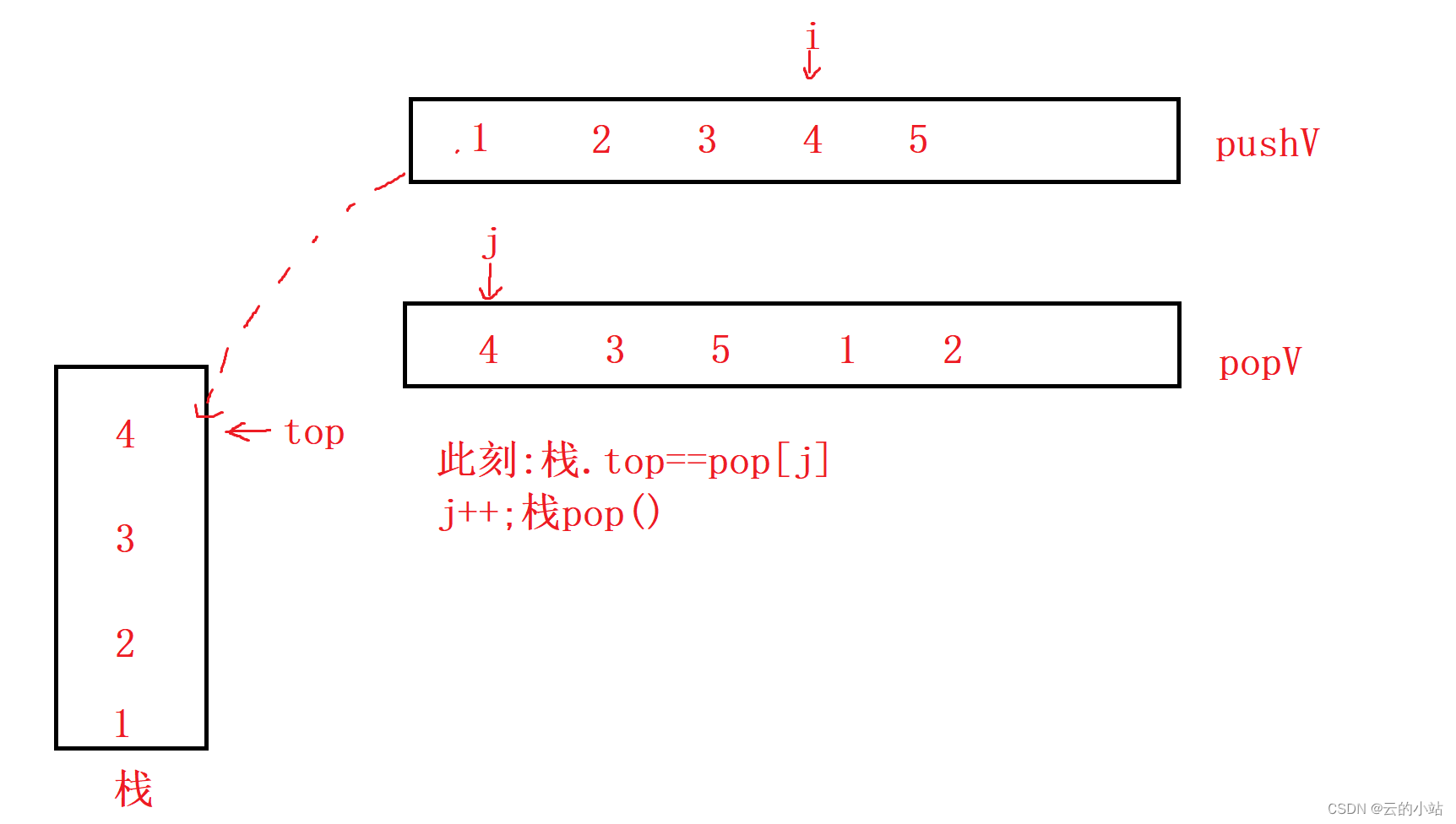
直到栈.top()等于popV[j]此刻将栈顶删除并且j++,并且检查新栈top是否等于popV[j ]
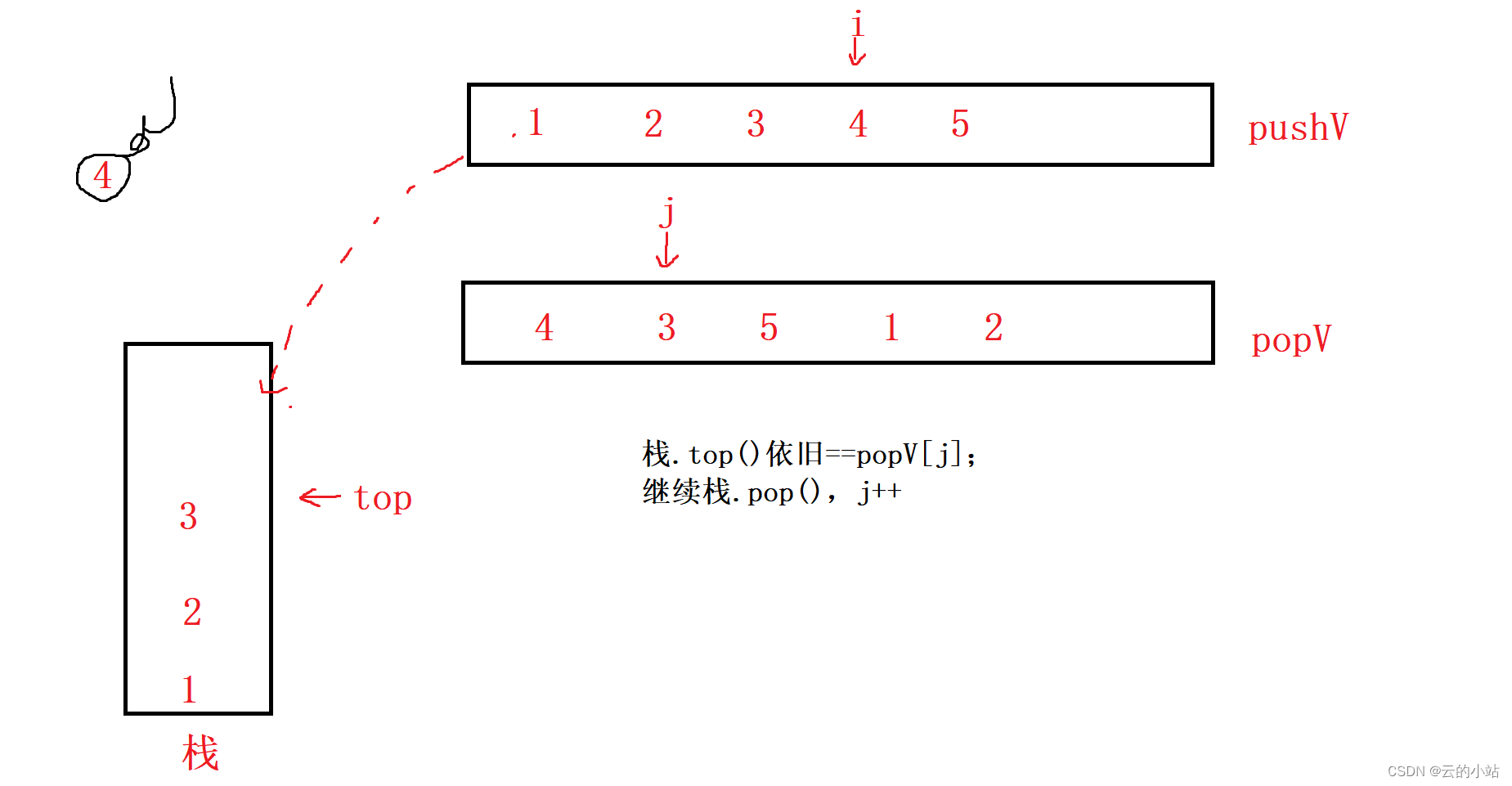
继续栈pop
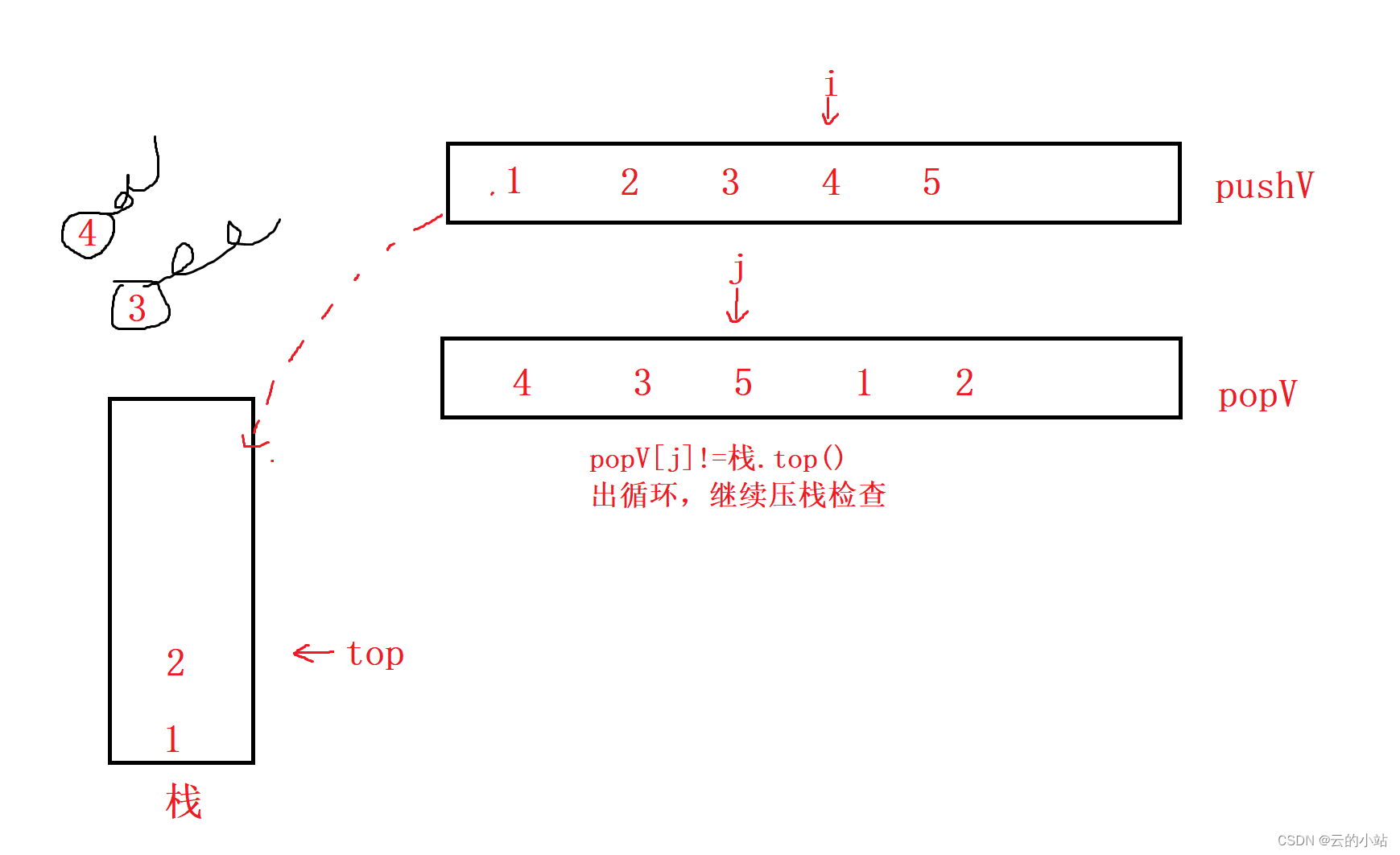

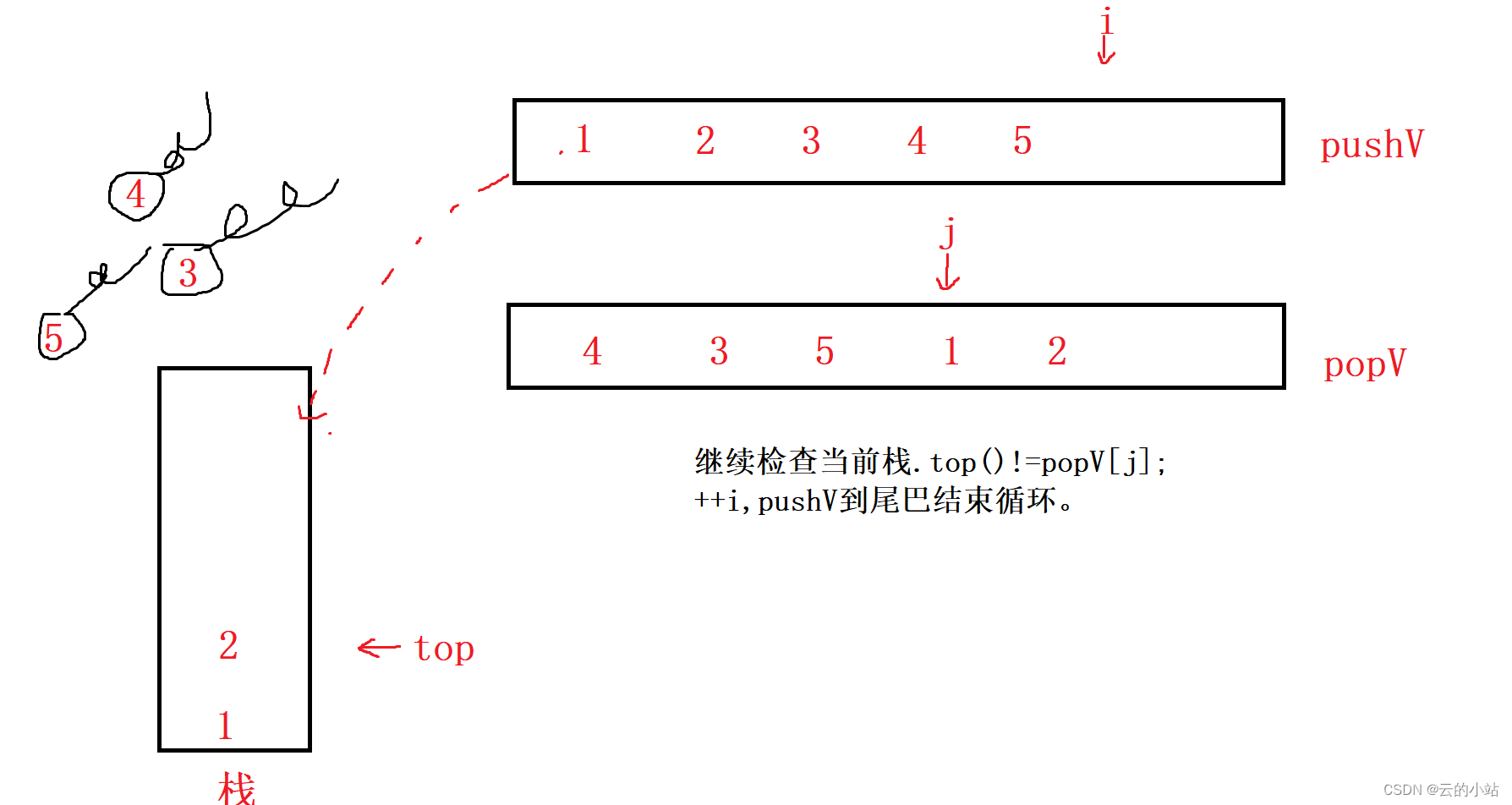
这个时候检查栈是否有数据,如果有数据就是错误的,如果没有数据就是正确的。
代码:
class Solution {
public:
bool IsPopOrder(vector<int> pushV,vector<int> popV) {
stack<int> st;
vector<int>::size_type j=0;
for(size_t i=0;i<pushV.size();++i)
{
st.push(pushV[i]);
while(!st.empty()&&popV[j]==st.top())
{
st.pop();
++j;
}
}
return st.empty();
}
};逆波兰表达式
150. 逆波兰表达式求值 - 力扣(Leetcode)
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
注意:
- 有效的算符为
'+'、'-'、'*'和'/'。 - 每个操作数(运算对象)都可以是一个整数或者另一个表达式。
- 两个整数之间的除法总是 向零截断 。
- 表达式中不含除零运算。
- 输入是一个根据逆波兰表示法表示的算术表达式。
- 答案及所有中间计算结果可以用 32 位 整数表示。
建一个栈,将数字字符串转换为整型然后存放到栈中,如果遇见运算符字符串,就将栈中取两个数据,进行运行,结果在压入栈中。
注意我们将使用switch判断表达式,表达式不可能比对字符串,但是可以比对整型字符char。所以我们将运算符字符串在比较时取第一个元素比较 char*ch="+" 取ch[0]进行比较。
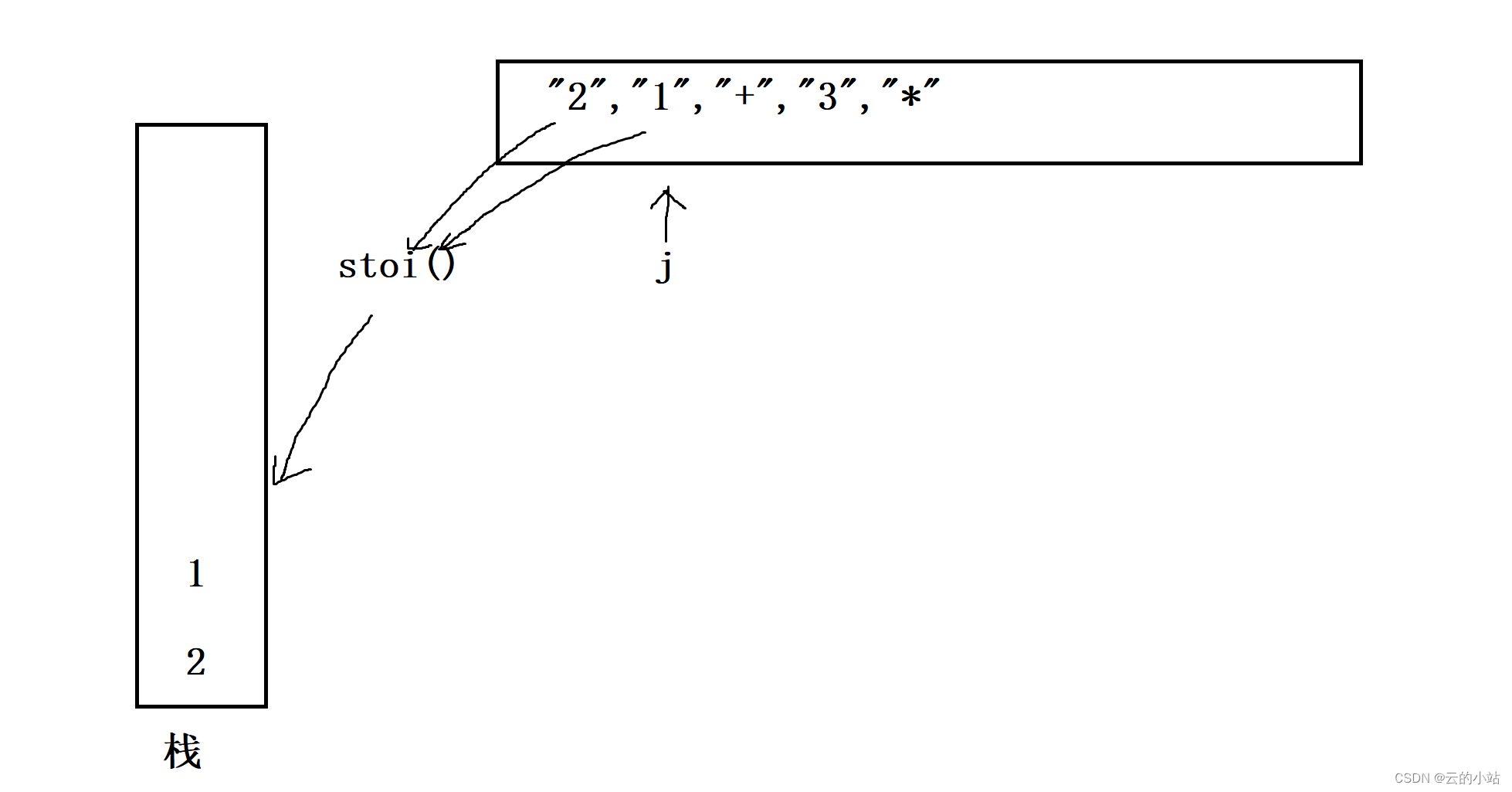
利用stoi函数将数字字符串转换为整型。

将“2” 和 “1”转换后压入栈中
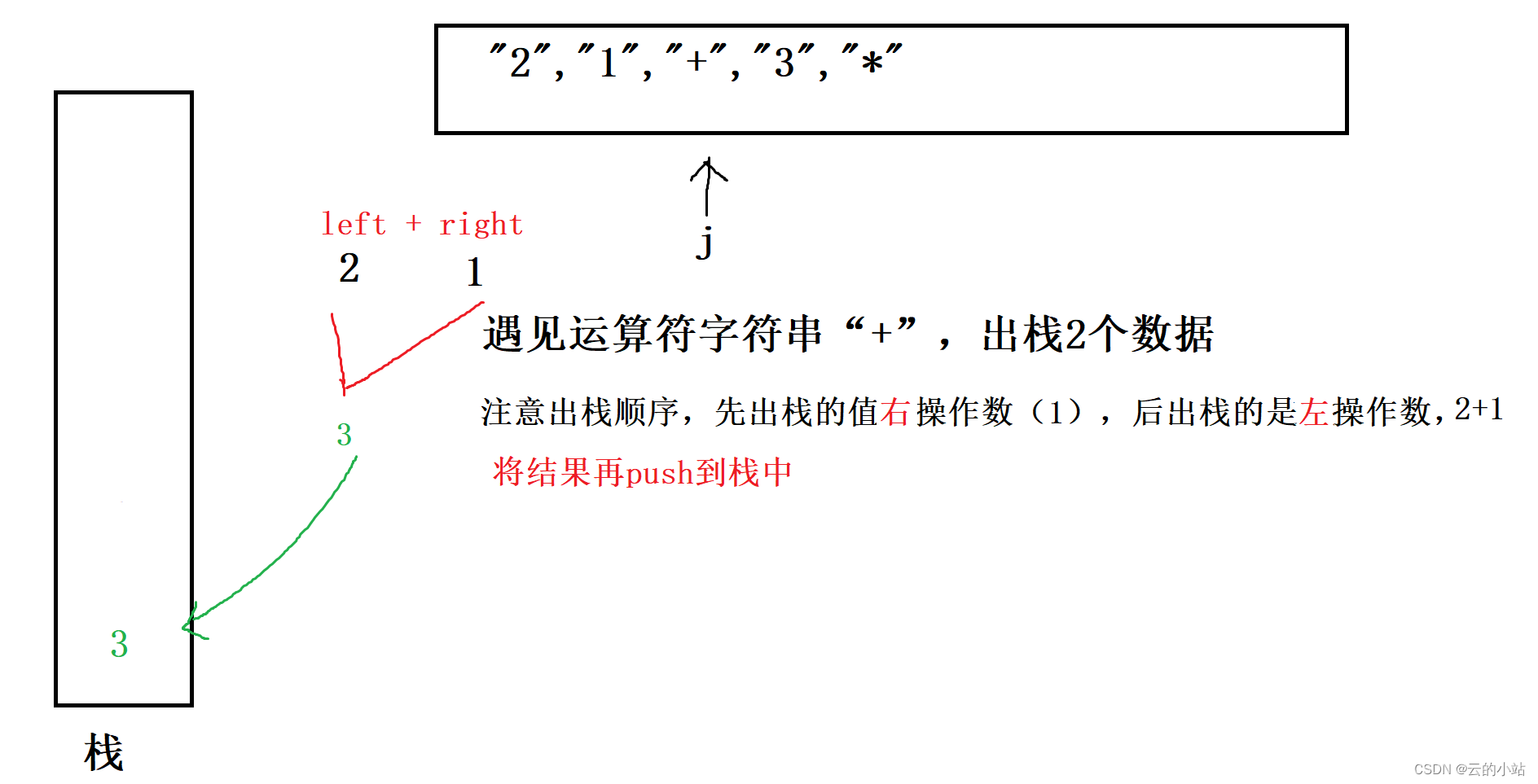
继续将字符串“5”压入栈中,
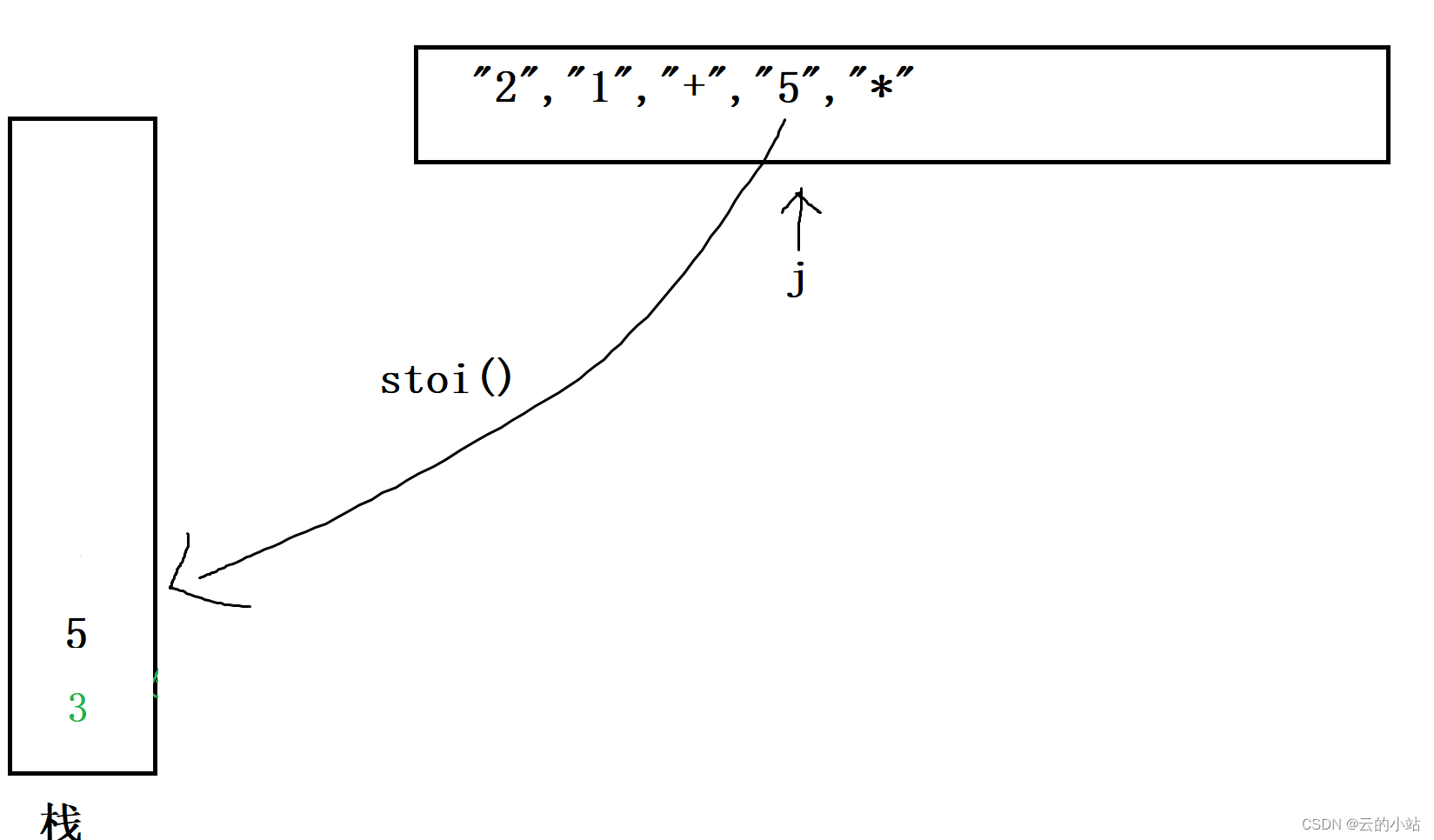
继续走遇见''*" 拿出数据5和3进行运算,5为右操作数,3为左操作数
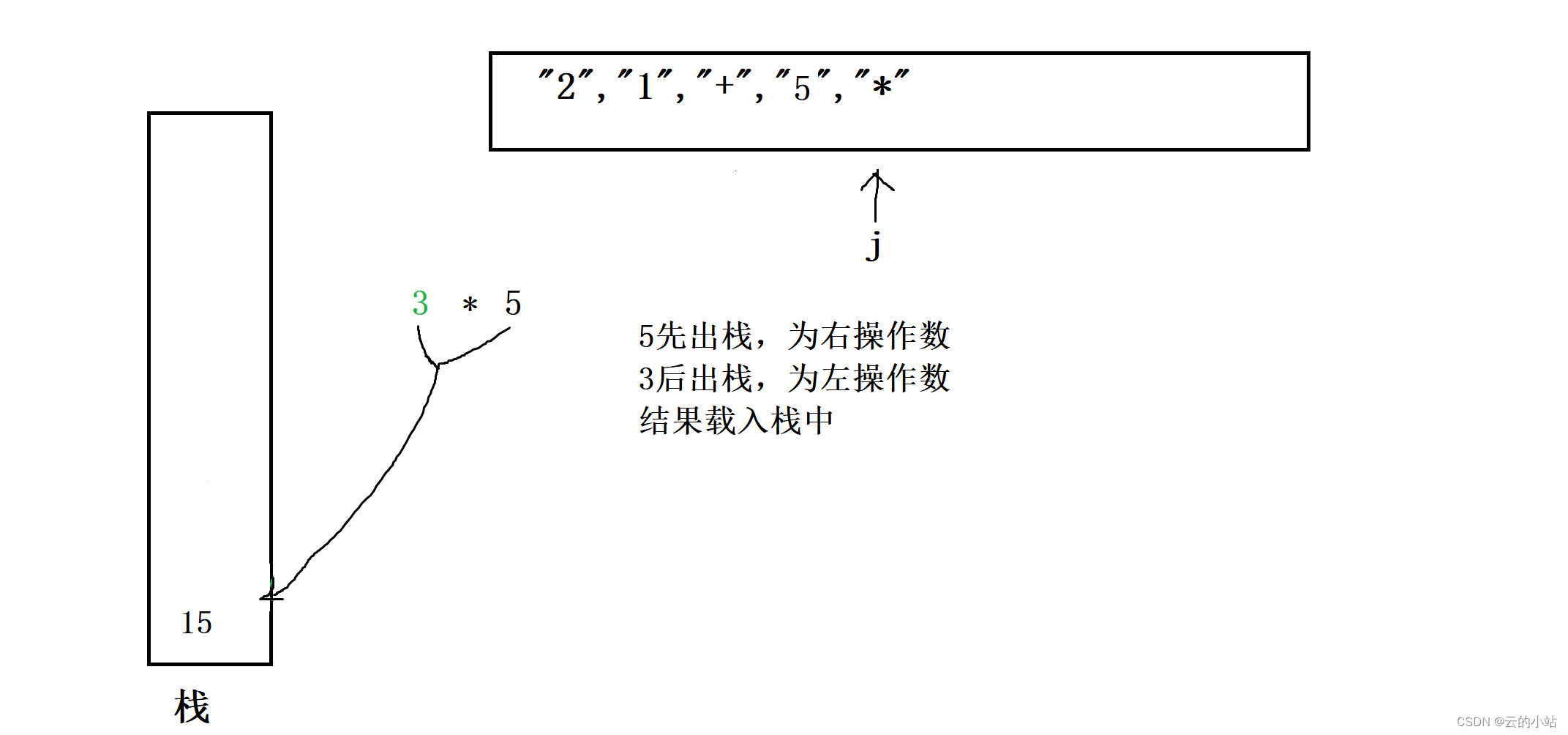
++j走到末尾,此刻将栈.top取出的数据就是结果数据
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> st;
for(auto ch : tokens)
{
if(ch=="+"||ch=="-"
||ch=="*"||ch=="/")
{
int num2=st.top();
st.pop();
int num1=st.top();
st.pop();
switch (ch[0]) {
case '+':
st.push(num1 + num2);
break;
case '-':
st.push(num1 - num2);
break;
case '*':
st.push(num1 * num2);
break;
case '/':
st.push(num1 / num2);
break;
}
}
else
{
st.push(stoi(ch));
}
}
return st.top();
}
};