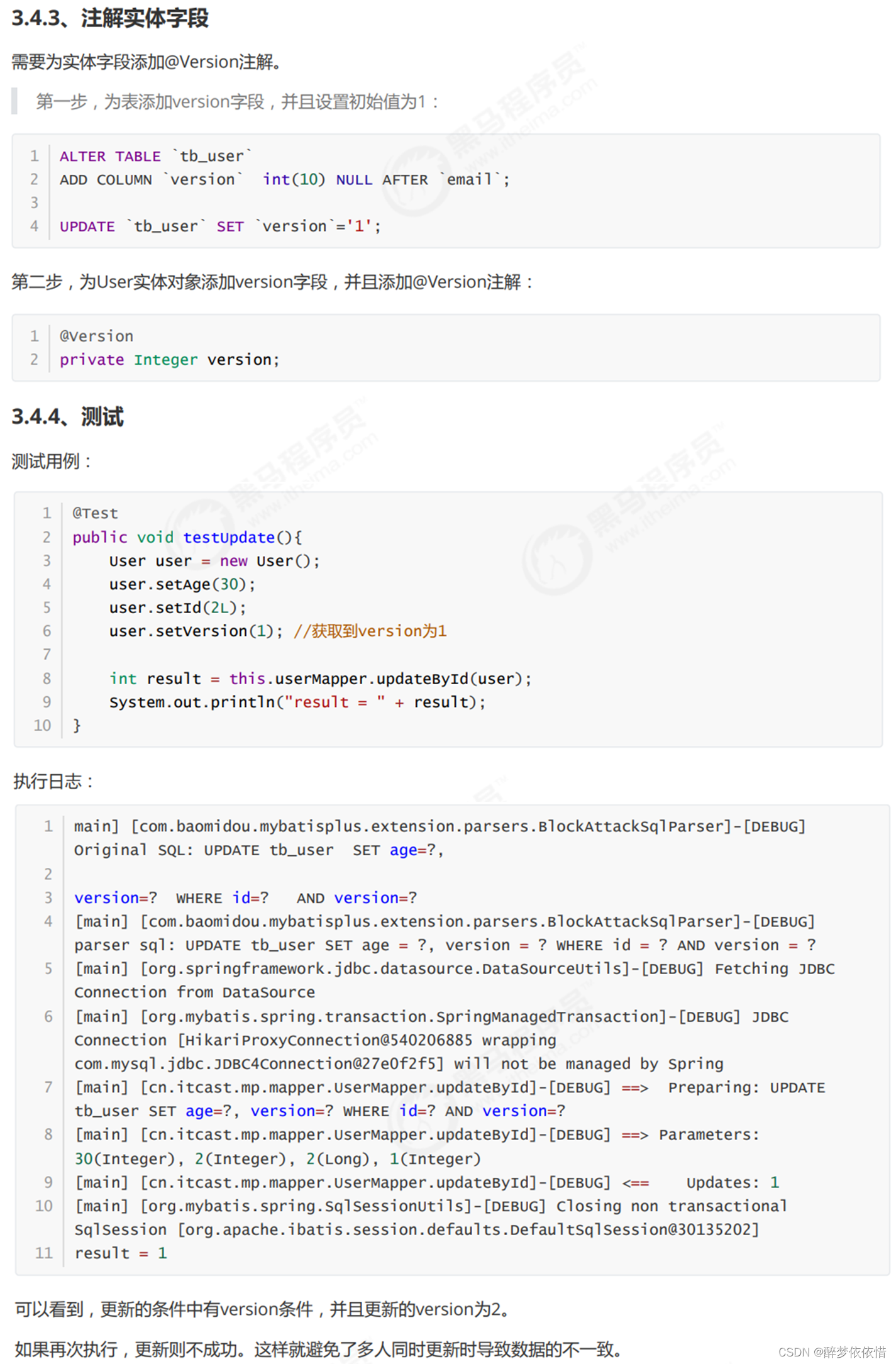
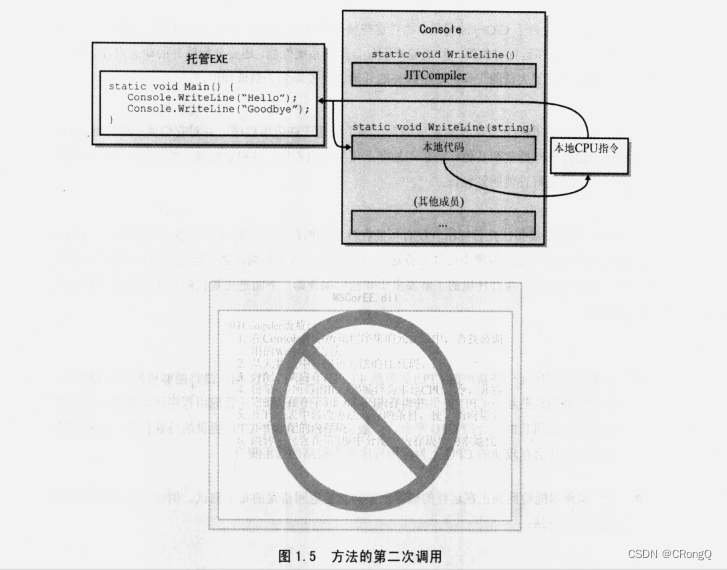
点到直线距离最小二乘解释

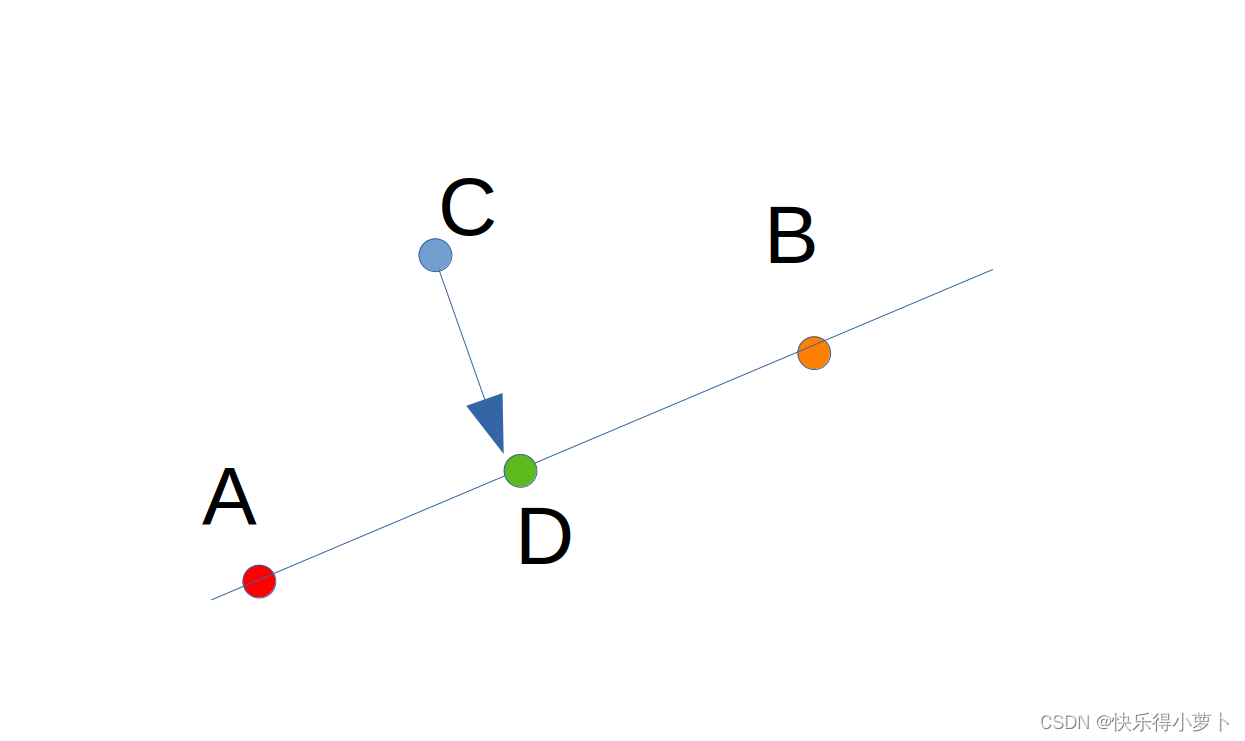
推倒部分

形象描述是C到AB距离最短，也就是CD最短用数学语言描述是$min||(B-A)\lambda +A-C||$ 其中 $D=(B-A)\lambda +A$,其实本质是一个最小二乘问题。因此带入得到
$$\lambda =((B-A{)}^T(B-A){)}^{-1}(B-A{)}^T(C-A)$$
因此带入得到$CD$
$$DC=C-[\lambda (B-A)+A]$$

实现代码

#include "bits/stdc++.h"
#include "eigen3/Eigen/Core"

// 求点到直线距离

using namespace std;

// 定义求解的模板类
// 目的求解C点到AB两点的距离

template<typename point>
class solve
{
private:
    point mPA;
    point mPB;
    point mPC;
public:
    // 求解的部分
    point getMinVec(bool isNeedCheck = false){
        point subBA = mPB - mPA;
        double inv = 1./(subBA.transpose()*subBA);
        double temp = (subBA.transpose()*(mPC-mPA));
        double lambda = inv * temp;
        point res = mPC - subBA * lambda - mPA;
        // 验证 点积为0,是垂直的状态
        if(isNeedCheck){
            cout << "check " << (res.transpose() * subBA).transpose() << endl;
        }
        return res;
    }
    solve(point _A, point _B, point _C):
    mPA(_A), mPB(_B), mPC(_C){

    }
    ~solve(){}
};


int main(int argc, char ** argv){

    
    // 例子1 求解两个2维度的点构成的线  与另一个点的距离
    Eigen::Matrix<double,2,1> iA(1,1);
    Eigen::Matrix<double,2,1> iB(2,2);
    Eigen::Matrix<double,2,1> iC(0,1);

    solve<Eigen::Matrix<double,2,1>> cal(iA, iB, iC);
    Eigen::Vector2d res = cal.getMinVec();
    cout << "2 维度向量：" << res.transpose() << endl;
    cout << "2 模长：" << res.norm() << endl;


    // 例子2 3维度的
    Eigen::Matrix<double, 3, 1> iA3(1, 1, 1);
    Eigen::Matrix<double, 3, 1> iB3(2, 2, 2);
    Eigen::Matrix<double, 3, 1> iC3(0, 1, 0);

    solve<Eigen::Matrix<double,3,1>> cal3(iA3, iB3, iC3);
    Eigen::Vector3d res3 = cal3.getMinVec(true);
    cout << "3 维度向量：" << res3.transpose() << endl;
    cout << "3 模长：" << res3.norm() << endl;


    return 0;



}