目录
1、堆的概念及结构
1.1 概念(概念总是重要的)
1.2 结构,分为两种
1.2.1 小堆/小根堆示例
1.2.2 大堆/大根堆示例
2、堆的接口
3、接口实现
3.1 堆的初始化
3.2 堆的销毁
3.3 堆的插入
功能分析:
功能实现:
3.4 堆的删除
功能分析:
功能实现:
3.5 取堆顶的数据
3.6 堆的数据个数
3.7 堆的判空
4、完整代码
1、堆的概念及结构
1.1 概念(概念总是重要的)

上面这一段是堆的概念,但是这也太没劲了吧,我们来通俗的讲一下,敲黑板了嗷:
堆的本质是一个完全二叉树。
大堆(也叫大根堆):父节点大于/等于子节点。
小对(也叫小根堆):父节点小于/等于子节点。
如果不满足上面的条件,那么就不是堆。
堆的性质:
1、堆中某个节点的值总是不大于或不小于其父节点的值;
2、堆总是一棵完全二叉树。
1.2 结构,分为两种
1.2.1 小堆/小根堆示例
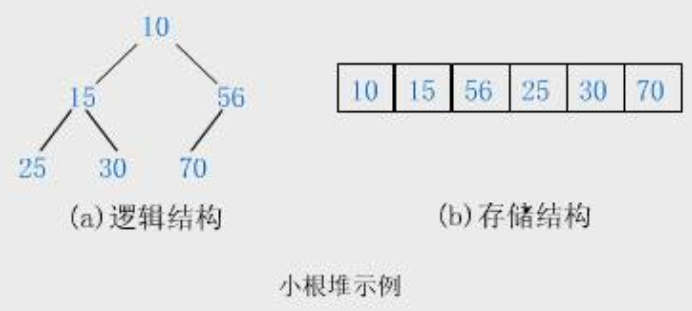
1.2.2 大堆/大根堆示例
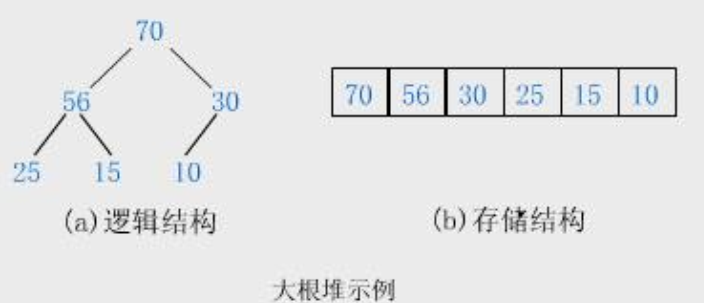
我们来看一个题目:
下列关键字序列为堆的是:(A)
A 100,60,70,50,32,65
B 60,70,65,50,32,100
C 65,100,70,32,50,60
D 70,65,100,32,50,60
E 32,50,100,70,65,60
F 50,100,70,65,60,32
分析:我们画图来分析
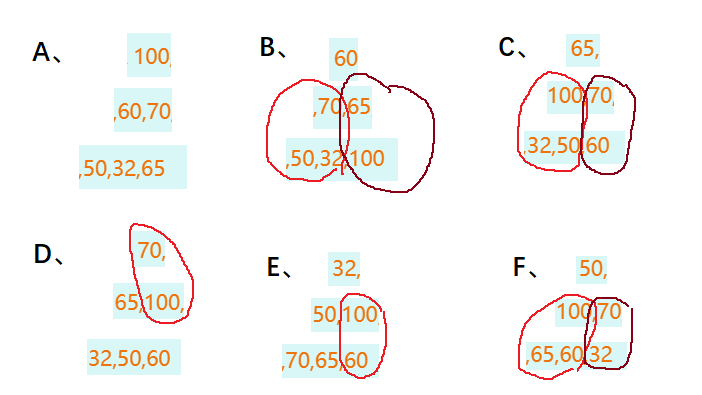
2、堆的接口
本篇文章是以小堆为例来实现的。堆的数据存储是用数组存的,数据的内存中的存储结构是顺序存储的,我们为了好理解,以逻辑结构理解的。
堆的接口有:初始化、销毁、插入、删除、取堆顶、堆的数据个数、判空。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
typedef int HPDataType;
typedef struct Heap
{
HPDataType* a;
int size;
int capacity;
}Heap;
// 堆的初始化
void HeapInit(Heap* hp);
// 堆的销毁
void HeapDestory(Heap* hp);
//交换
void Swap(HPDataType* p1, HPDataType* p2);
//向上调整
void AdjustUp(HPDataType* a, int child);
//向下调整
void AdjustDown(HPDataType* a, int size, int parent);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
bool HeapEmpty(Heap* hp);3、接口实现
我们这些接口好多都是与之前的数据结构文章是类似的,前面已经多次讲解,这里就不再讲解了,要是有看不懂的地方可以参考之前的数据结构文章。
3.1 堆的初始化
void HeapInit(Heap* hp)
{
assert(hp);
hp->a = NULL;
hp->size = 0;
hp->capacity = 0;
}3.2 堆的销毁
void HeapDestory(Heap* hp)
{
assert(hp);
free(hp->a);
hp->a = NULL;
hp->size = hp->capacity = 0;
}3.3 堆的插入
堆的插入是比较复杂的,也是一个难点,我们先来分析,再去实现功能。
功能分析:
1、插入的时候我们先要看数组是否需要扩容,先判满,如果空间满了就先扩容,然后将新元素插入到数组的尾部;
2、我们新插入一个元素,就需要去分析一下此堆是否满足小堆的结构,如果不满足我们就需要将新元素向上调整。
3、向上调整过程分析:
我们来举例分析一下:如果给一个小堆插入一个元素后,堆的结构被破坏,如何调整才能恢复小堆的结构。
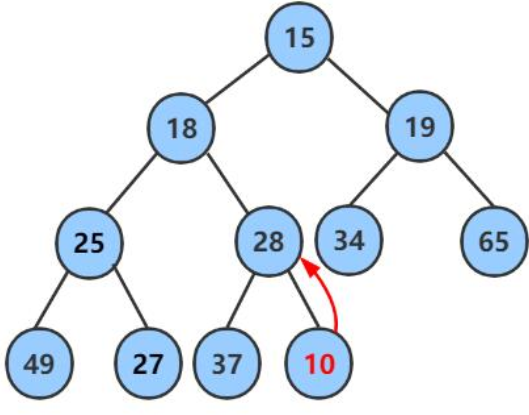
a、当我们发现给小堆插入一个 10 后,10 比父节点 28 小,破坏了小堆的结构,我们需要对堆进行调整;
b、堆的物理结构是数组,所以我们可以通过下标来找到父节点,这里找父节点的公式:parent = (child-1)/2。当我们找到父节点后,让子节点与父节点去比较,如果小于父节点我们就让两个节点的元素交换,交换后的父节点与它的父节点可能也不满足小堆,因此需要不断的向上调整;
c、循环去比较调整,当child = 0 时,我们的调整就结束了,因此我们的循环判断条件为 child > 0。
注意:当有一次调整完后,我们的堆已经成为了小堆,就跳出循环。
我们根据上面的思路来画图走一遍:
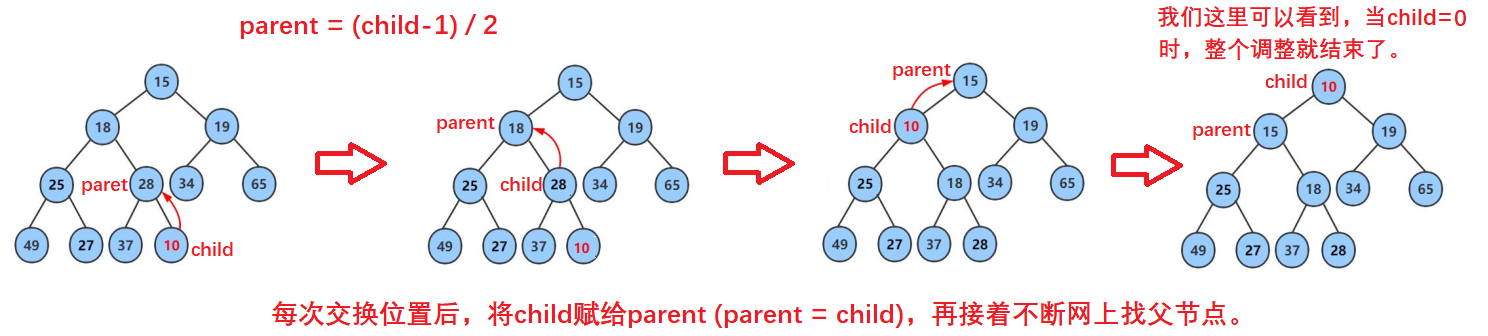
我们对功能的分析就结束了,开始实现功能。
功能实现:
void Swap(HPDataType* p1, HPDataType* p2)
{
HPDataType tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void AdjustUp(HPDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] < a[parent])//这里控制大小堆
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
//log N
void HeapPush(Heap* hp, HPDataType x)
{
assert(hp);
if (hp->size == hp->capacity)
{
int newcapacity = hp->capacity == 0 ? 4 : 2 * hp->capacity;
HPDataType* tmp = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * newcapacity);
if (NULL == tmp)
{
perror("realloc fail:");
}
hp->a = tmp;
hp->capacity = newcapacity;
}
hp->a[hp->size] = x;
hp->size++;
AdjustUp(hp->a, hp->size - 1);
}交换与向上调整后面我们会复用的,因此我们将其两个功能封装成函数。
3.4 堆的删除
堆的删除是删堆顶的元素。
思路:堆顶数据与最后一个数据交换,删掉最后一个数据,再从堆顶向下调整。
功能分析:
我们这里删除堆顶数据的时候不能直接删,直接删除堆顶数据就会破坏堆结构,再去建堆时间复杂度太高,不推荐,这里我们介绍一种方法,复杂度较低:
1、我们将堆顶数据与最后一个数据先交换,再删除最后一个数据,最后从堆顶向下调整;
2、向下调整比较复杂,我们下面进行分析并画图来讲解:
a、此时我们的 parent节点 是堆顶节点,接下来我们需要找到 2 个子节点中小的哪个作为孩子节点,这里的找子节点公式:child = parent*2 + 1;
b、如果孩子小于父亲,就交换,并且继续往下调整,让parent 走到 child 位置,再去算 child 位置;
c、当孩子下标大于数组的大小时,循环就结束,整个调整就完成了。
注意:当有一次调整完后,我们的堆已经成为了小堆,就跳出循环。
功能实现:
void AdjustDown(HPDataType* a, int size, int parent)
{
int child = parent * 2 + 1;
while (child < size)//当child大于了数组大小就跳出循环
{
//找出左右孩子中小/大的那个(假设法)
if (child + 1 < size && a[child + 1] < a[child])
{
child++;
}
if (a[child] < a[parent])
{
Swap(&a[parent], &a[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//log N
void HeapPop(Heap* hp)
{
assert(hp);
assert(!HeapEmpty(hp));
Swap(&hp->a[0], &hp->a[hp->size - 1]);
hp->size--;
AdjustDown(hp->a, hp->size, 0);
}3.5 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{
assert(hp);
assert(!HeapEmpty(hp));
return hp->a[0];
}3.6 堆的数据个数
int HeapSize(Heap* hp)
{
assert(hp);
assert(!HeapEmpty(hp));
return hp->size;
}3.7 堆的判空
bool HeapEmpty(Heap* hp)
{
assert(hp);
return hp->size == 0;
}4、完整代码
完整代码在代码仓库:Heap · 小白在努力jy/DataStructure - 码云 - 开源中国 (gitee.com)