来源:力扣(LeetCode)
描述:
给你一个 n x n 的二进制矩阵 grid 中,返回矩阵中最短 畅通路径 的长度。如果不存在这样的路径,返回 -1 。
二进制矩阵中的 畅通路径 是一条从 左上角 单元格(即,(0, 0))到 右下角 单元格(即,(n - 1, n - 1))的路径,该路径同时满足下述要求:
- 路径途经的所有单元格都的值都是
0。 - 路径中所有相邻的单元格应当在 8 个方向之一 上连通(即,相邻两单元之间彼此不同且共享一条边或者一个角)。
畅通路径的长度 是该路径途经的单元格总数。
示例 1:
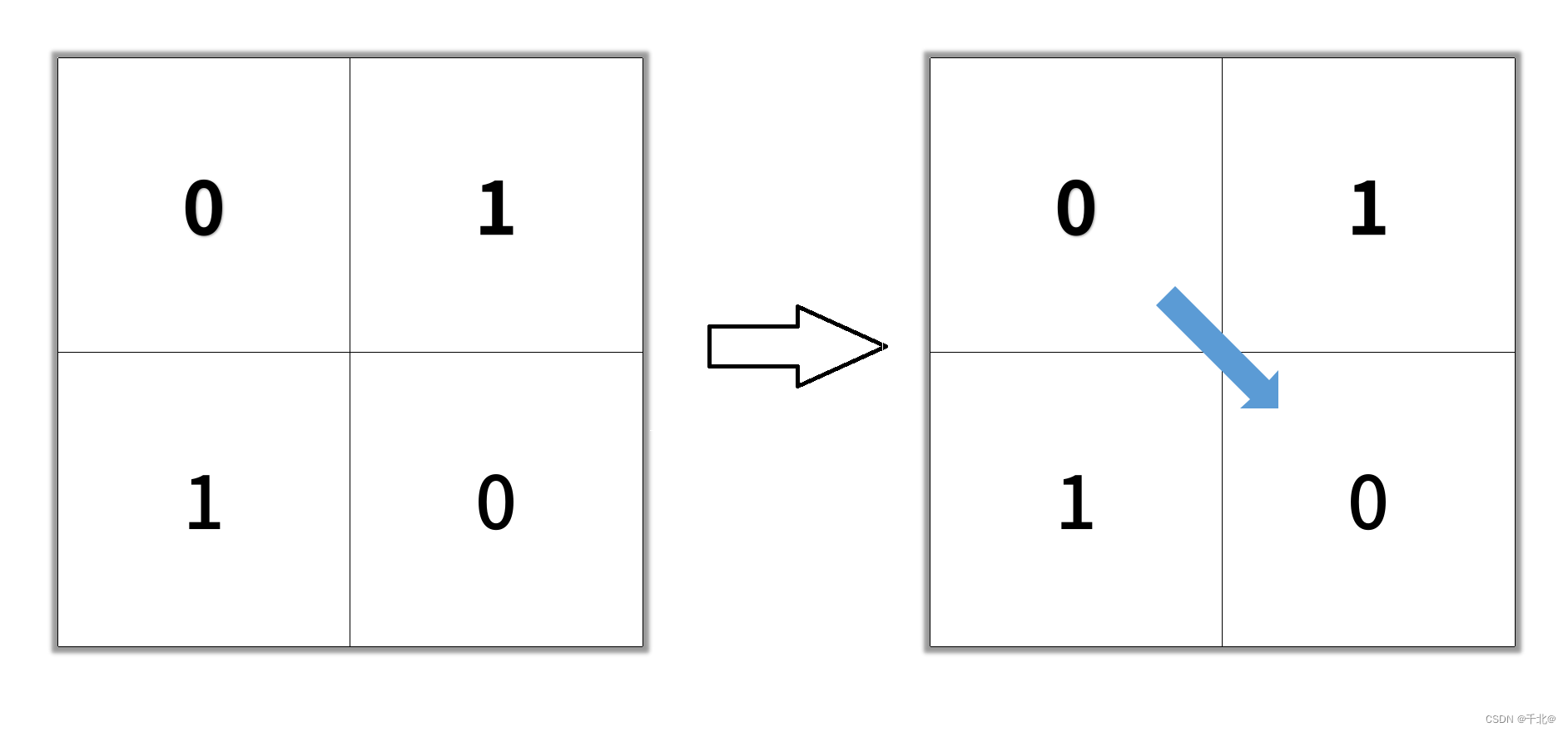
输入:grid = [[0,1],[1,0]]
输出:2
示例 2:
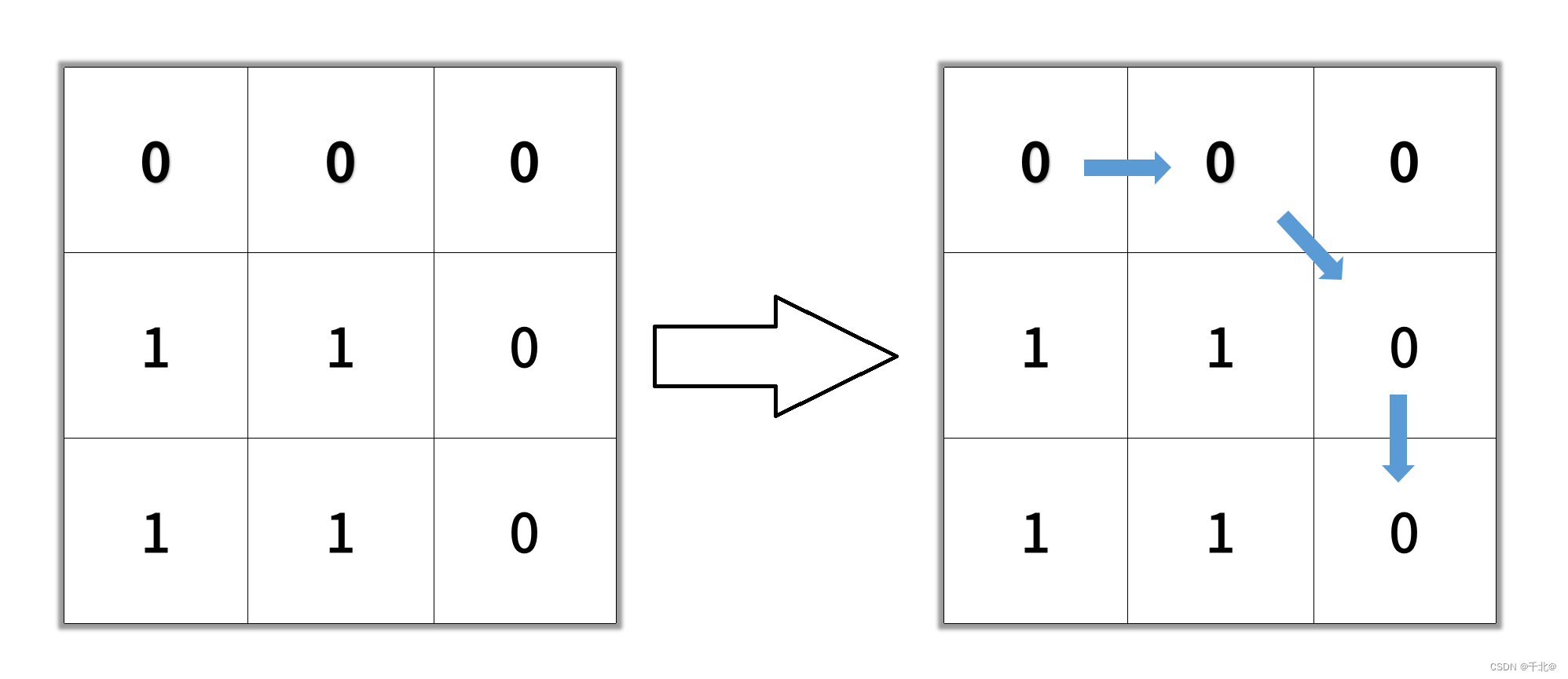
输入:grid = [[0,0,0],[1,1,0],[1,1,0]]
输出:4
示例 3:
输入:grid = [[1,0,0],[1,1,0],[1,1,0]]
输出:-1
提示:
- n == grid.length
- n == grid[i].length
- 1 <= n <= 100
- grid[i][j] 为 0 或 1
方法:广度优先搜索
把单元格当成图的节点,如果两个相邻单元格的值都是 0,那么这两个相邻单元格代表的节点之间存在边,且边长为 1。因此问题可以转化为给定一个无权图,求两个节点的最短路径。求无权图的最短路径问题的解法是广度优先搜索。
首先如果 grid[0][0] = 1,那么显然不存在最短路径,因此返回 −1。使用 dist 保存某一单元格到左上角单元格的最短路径,初始时 dist[0][0] = 0。初始时,我们将单元格 (0, 0) 放入队列中,然后不断执行以下操作:
- 如果队列为空,那么返回 −1。
- 从队列中取出单元格 (x, y),如果该单元格等于右上角单元格,那么返回 dist[x][y]。
- 遍历该单元格的所有相邻单元格,如果相邻单元格 (x1, y1) 的值为 0 且未被访问,那么令 dist[x1][y1] = dist[x][y] + 1,并且将相邻单元格 (x1, y1) 放入队列中。
代码:
class Solution {
public:
int shortestPathBinaryMatrix(vector<vector<int>>& grid) {
if (grid[0][0] == 1) {
return -1;
}
int n = grid.size();
vector<vector<int>> dist(n, vector<int>(n, INT_MAX));
queue<pair<int, int>> q;
q.push({0, 0});
dist[0][0] = 1;
while (!q.empty()) {
auto [x, y] = q.front();
q.pop();
if (x == n - 1 && y == n - 1) {
return dist[x][y];
}
for (int dx = -1; dx <= 1; dx++) {
for (int dy = -1; dy <= 1; dy++) {
if (x + dx < 0 || x + dx >= n || y + dy < 0 || y + dy >= n) { // 越界
continue;
}
if (grid[x + dx][y + dy] == 1 || dist[x + dx][y + dy] <= dist[x][y] + 1) { // 单元格值不为 0 或已被访问
continue;
}
dist[x + dx][y + dy] = dist[x][y] + 1;
q.push({x + dx, y + dy});
}
}
}
return -1;
}
};
执行用时:56 ms, 在所有 C++ 提交中击败了50.27%的用户
内存消耗:20.2 MB, 在所有 C++ 提交中击败了32.54%的用户
复杂度分析
时间复杂度:O(n2),其中 n 是数组的行数或列数。广度优先搜索最多访问 n2 个单元格。
空间复杂度:O(n2)。队列 q 不超过 n2 个元素,保存 dist 需要 O(n2) 的空间,保存队列 q 需要 O(n2) 的空间。
author:LeetCode-Solution