CNN详细学习

news2024/10/6 20:36:43

前馈神经网络

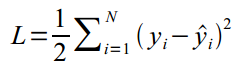
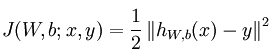
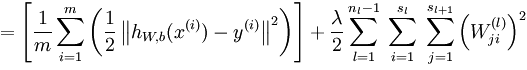
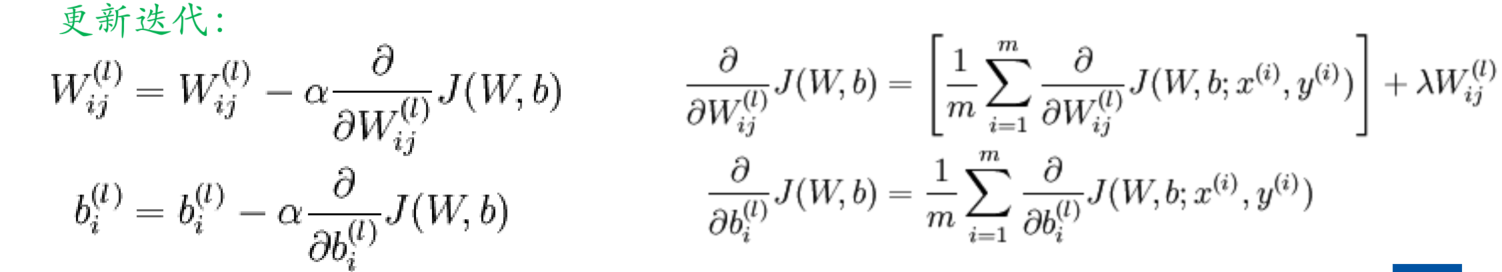
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

常见激活函数

  • sigmoid函数
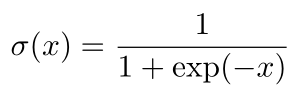
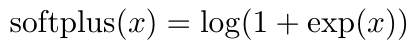
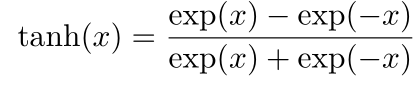
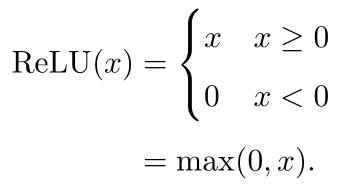
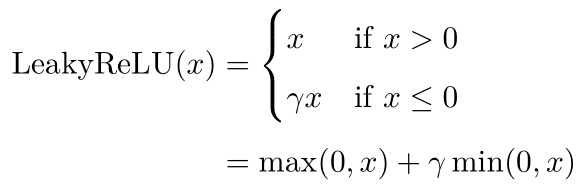
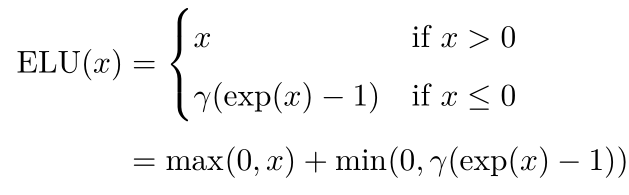
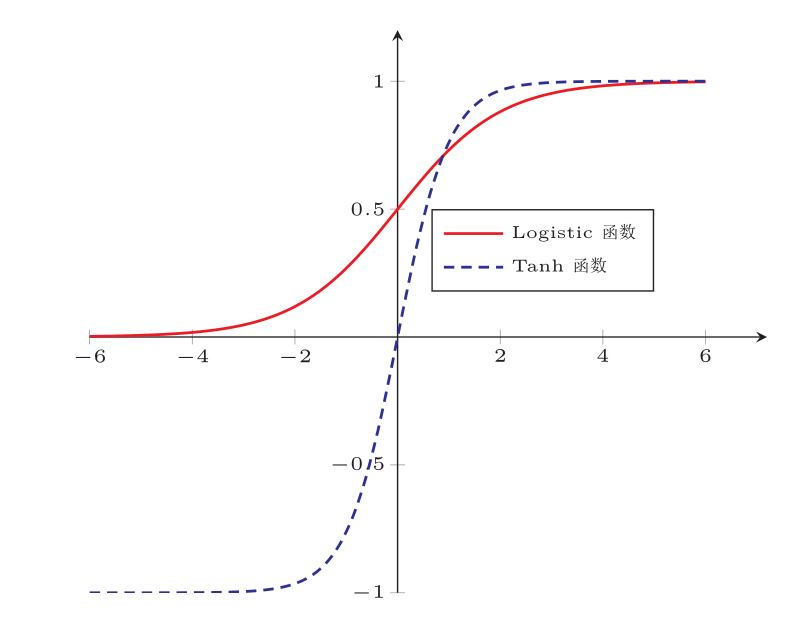
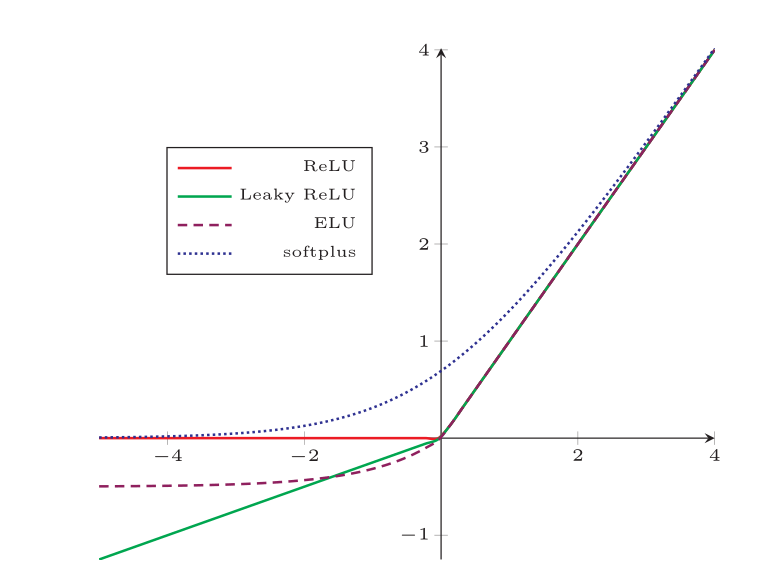
    在这里插入图片描述
    在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

梯度消失与爆炸

在这里插入图片描述

通用逼近定理

在这里插入图片描述
根据通用近似定理，对于具有线性输出层和至少一个使用“挤压”性质的激活函数的隐藏层组成的前馈神经网络

  • 只要其隐藏层神经元的数量足够，它可以以任意的精度来近似任何从一个定义在实数空间中的有界闭集函数。
  • 隐含层的数量不是越多越好，层数和特征的个数太多，会造成优化的难度和出现过拟合的现象
  • 只需要输入最基本的特征x1, x2, 只要给予足够多层的神经网络和神经元，神经网络会自己组合出最有用的特征

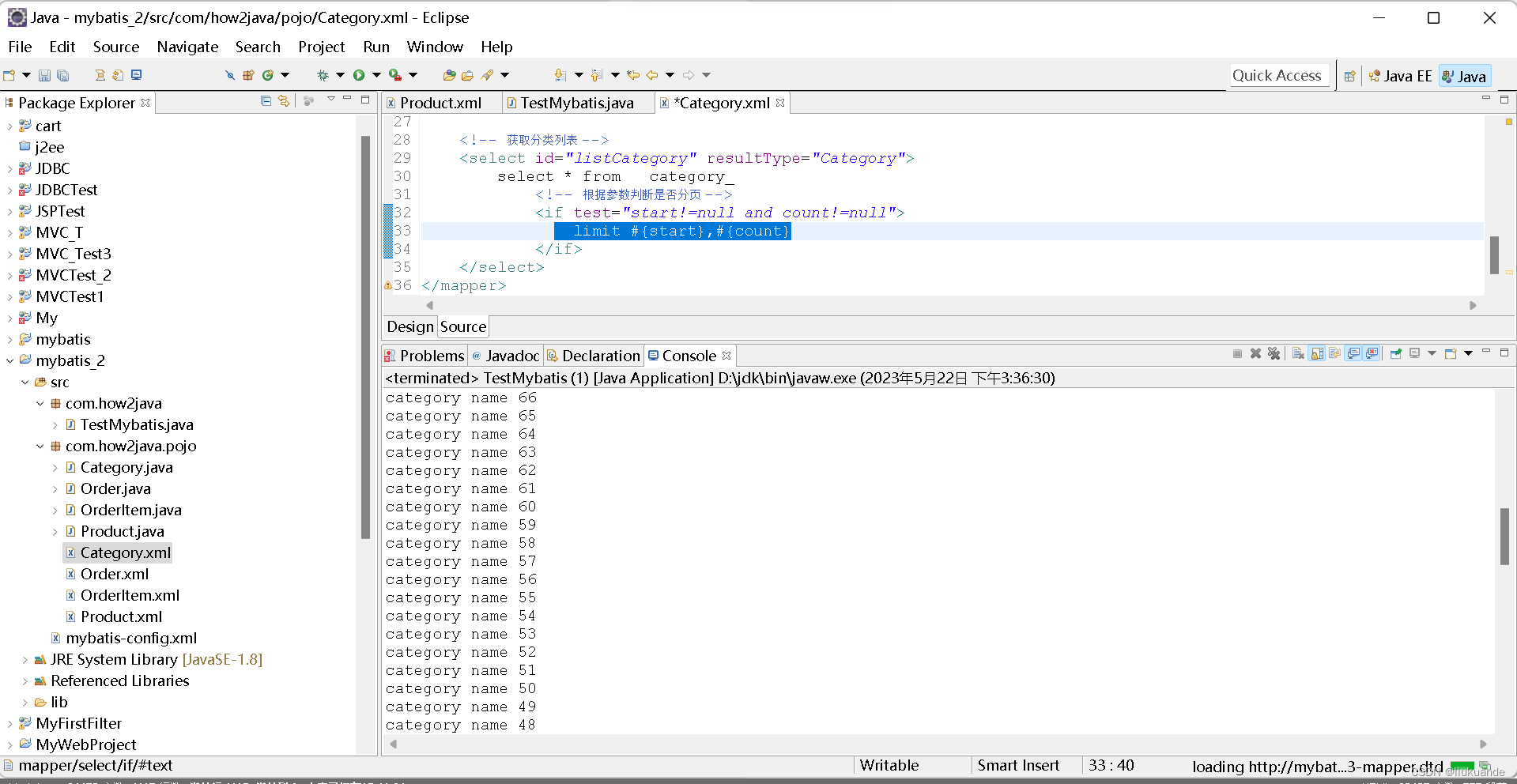
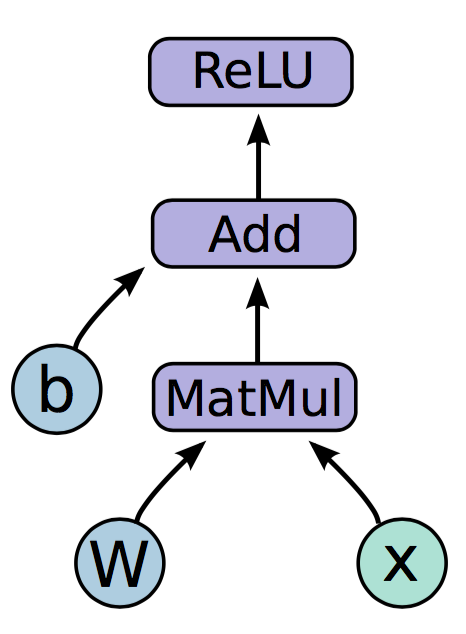
tensorflow实现

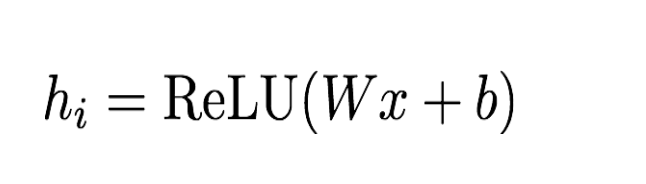
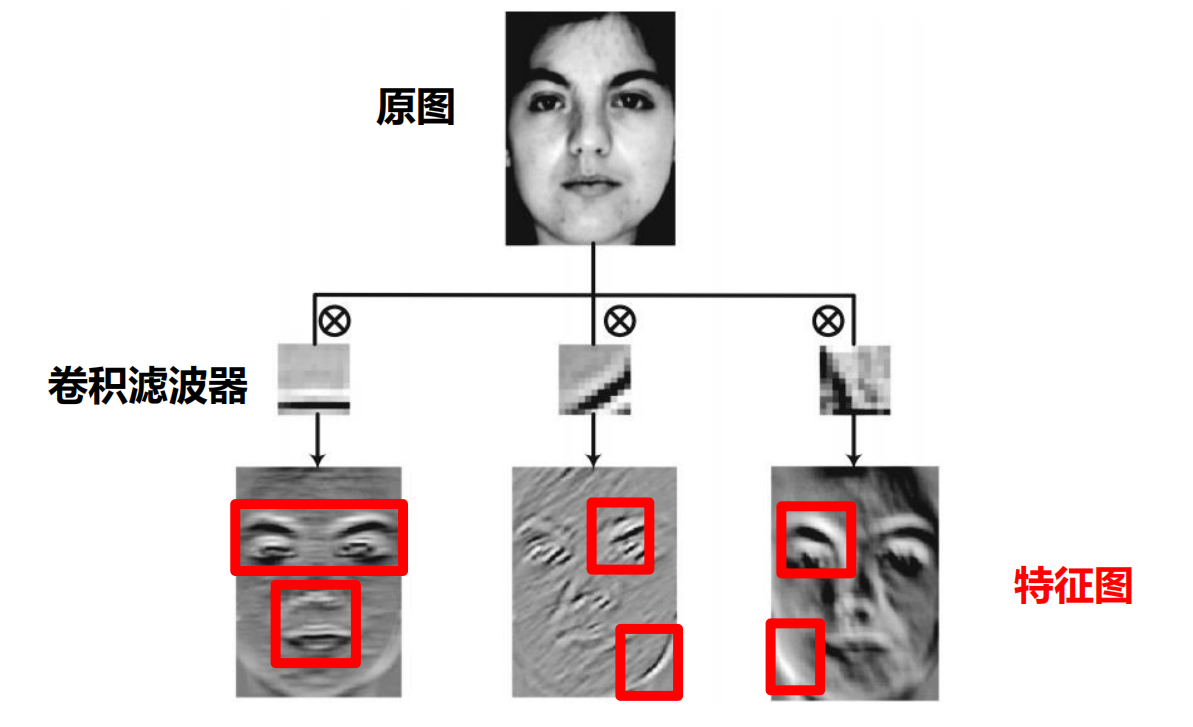
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

  • 一张图片-个滤波器，得一个特征图
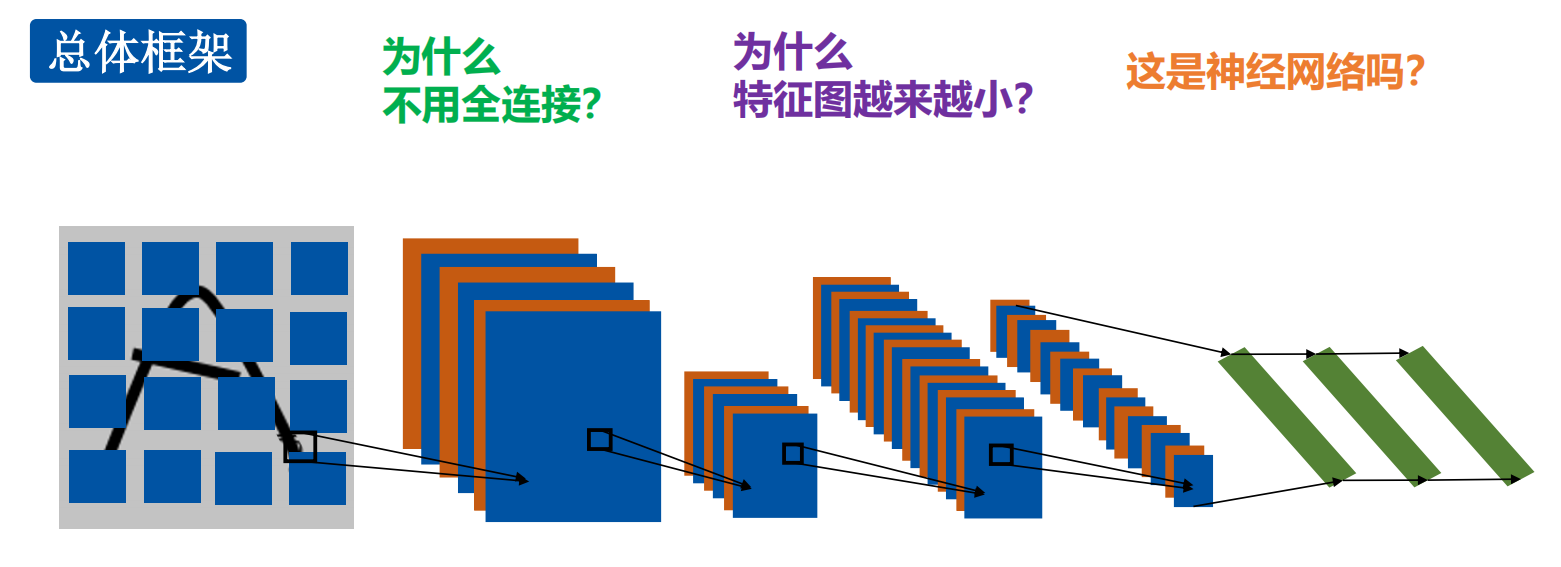
    在这里插入图片描述
    在这里插入图片描述
  • 为什么不用全连接？计算量太大，容易过拟合
  • 为什么特征图越来越小? 下采样，即池化会让特征图尺寸变小
  • 这是神经网络么？是的

CNN的由来：

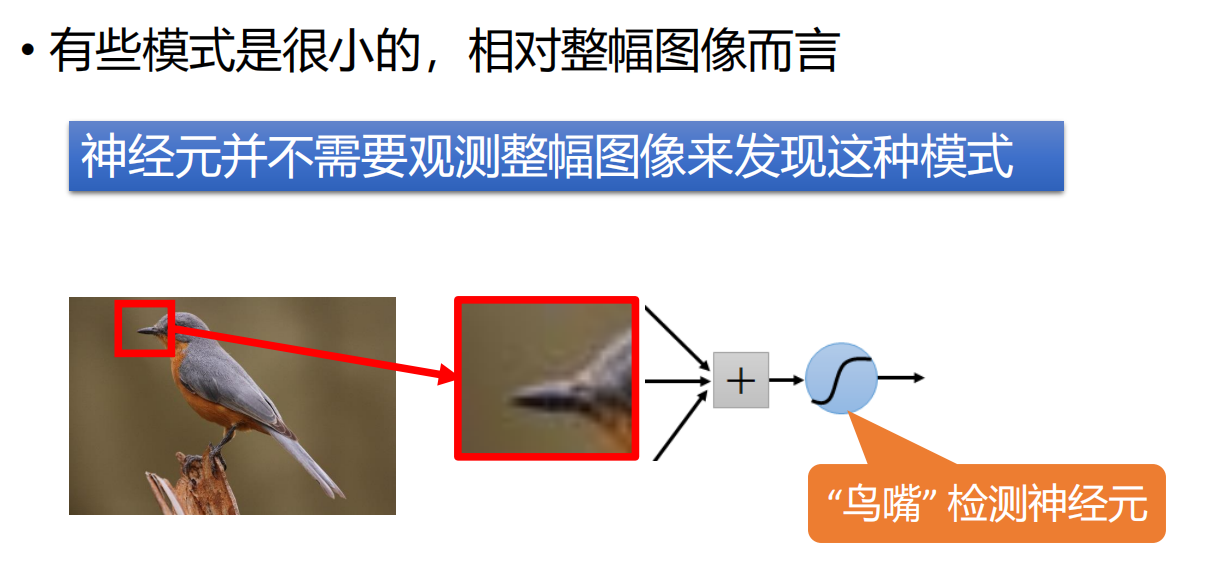
在这里插入图片描述

  • 引出，CNN的第一个特点：局部感知
    在这里插入图片描述
    在这里插入图片描述
  • 引导出第二个特征：权重共享

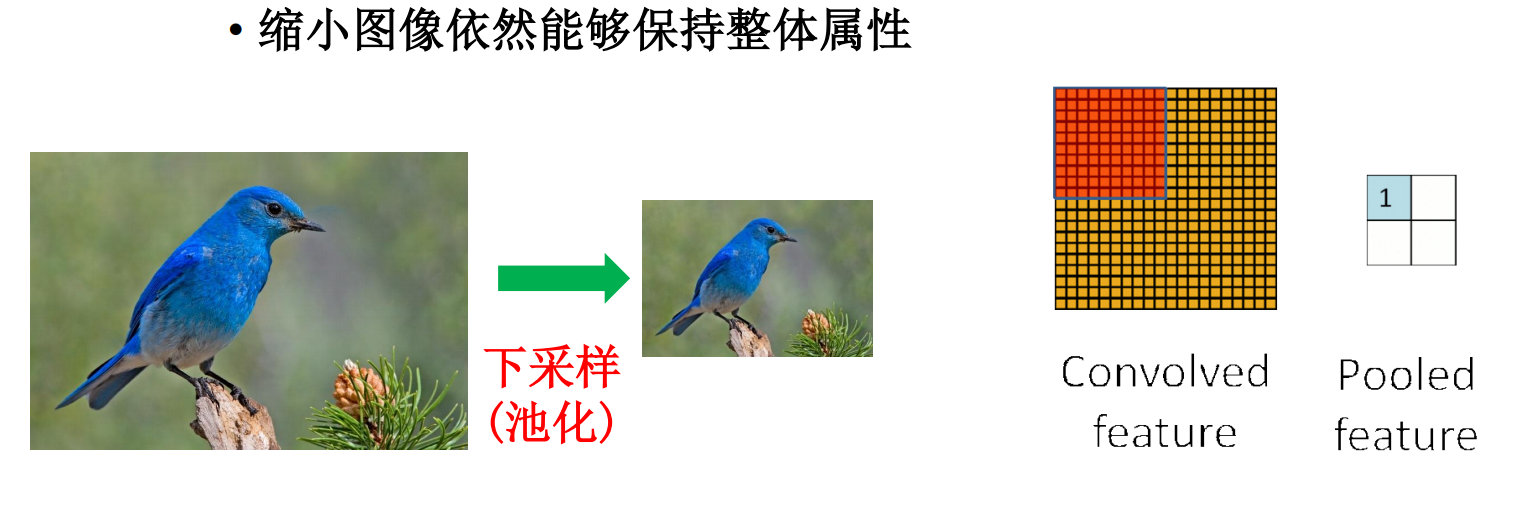
在这里插入图片描述

  • 第三个特征：池化，下采样

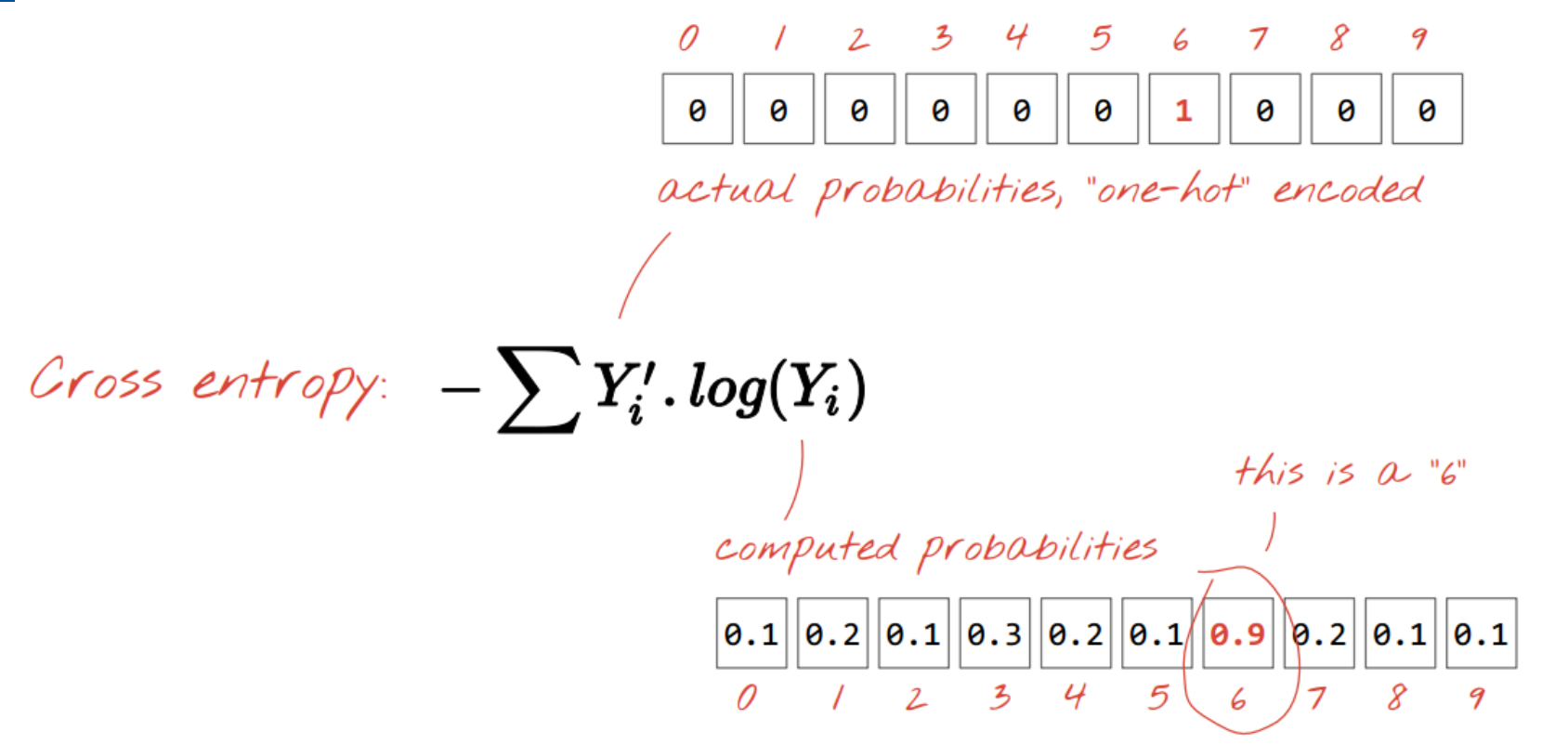
全连接网络的BP算法

  • 模型函数表达式
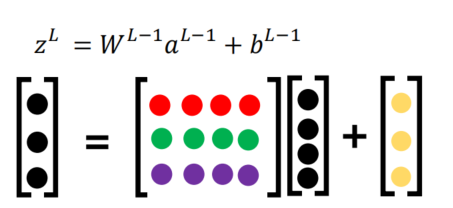
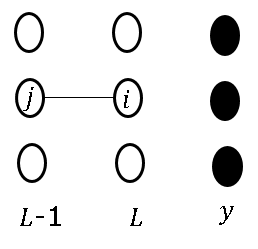
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
  • 带上损失函数进行求导
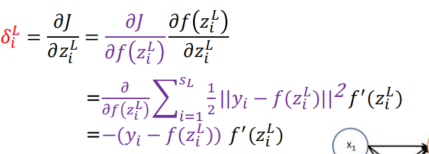
    在这里插入图片描述
  • L-2层同理
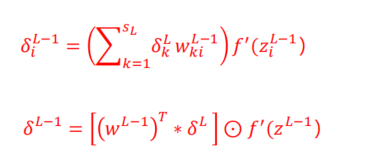
    在这里插入图片描述在这里插入图片描述
    在这里插入图片描述

CNN的卷积BP算法

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

  • δ \delta δ是误差矩阵
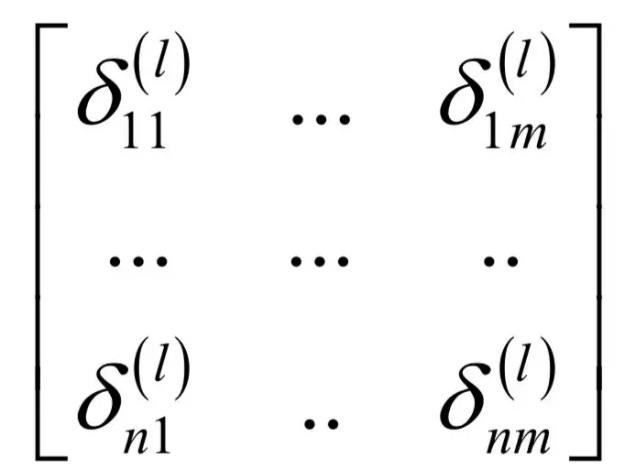
    在这里插入图片描述
    在这里插入图片描述

残差如何传递？

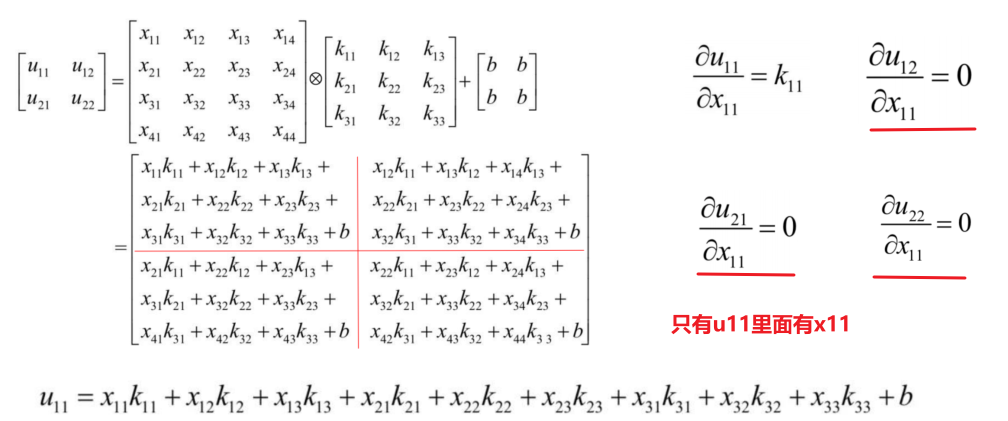
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

δ \delta δ求解详细过程

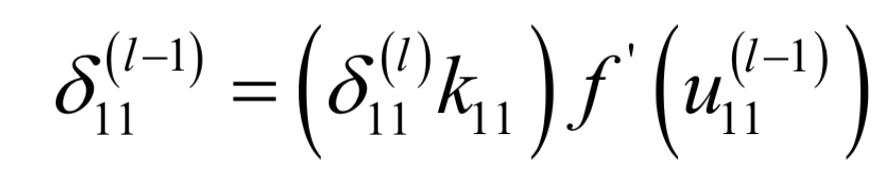
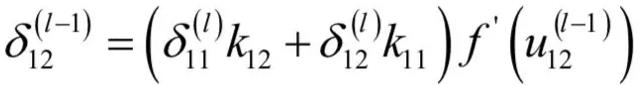
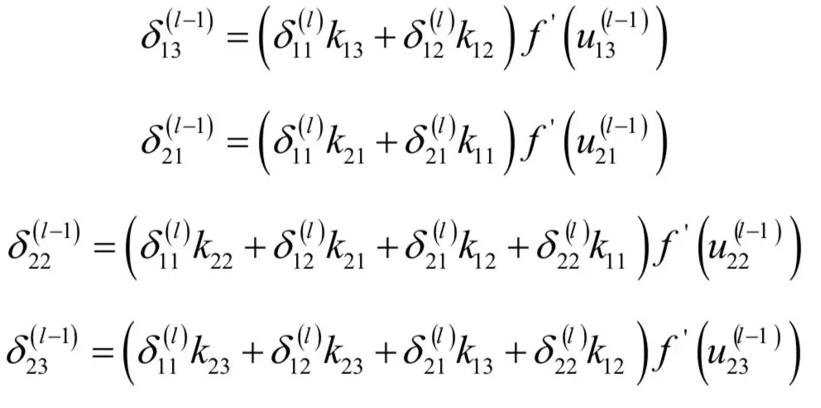
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

  • 关键核心公式
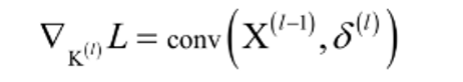
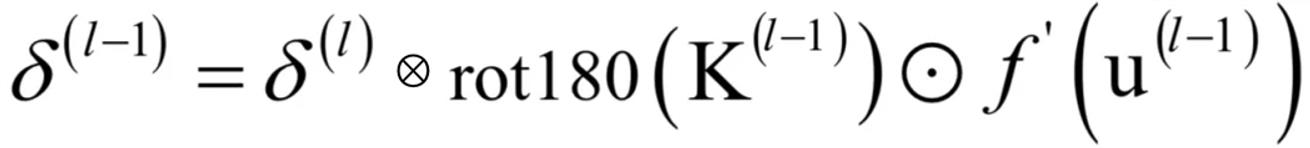
    在这里插入图片描述
    在这里插入图片描述
  • 误差项，求完导是1，所以残差项传递与bias项无关
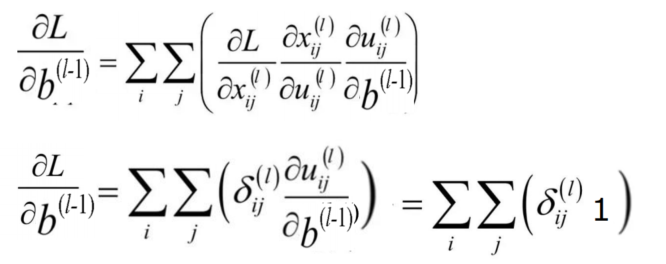
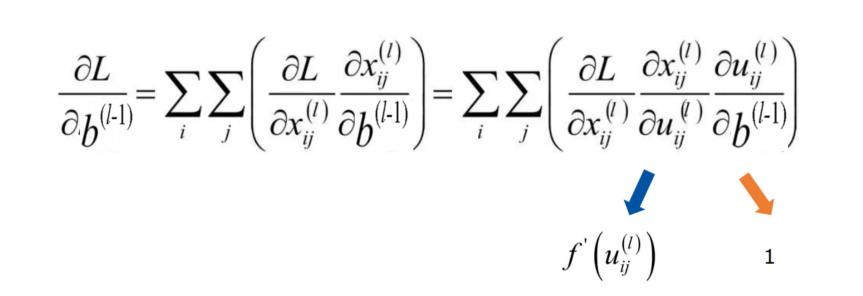
    在这里插入图片描述
    在这里插入图片描述
  • 多个特征图可以并行卷积
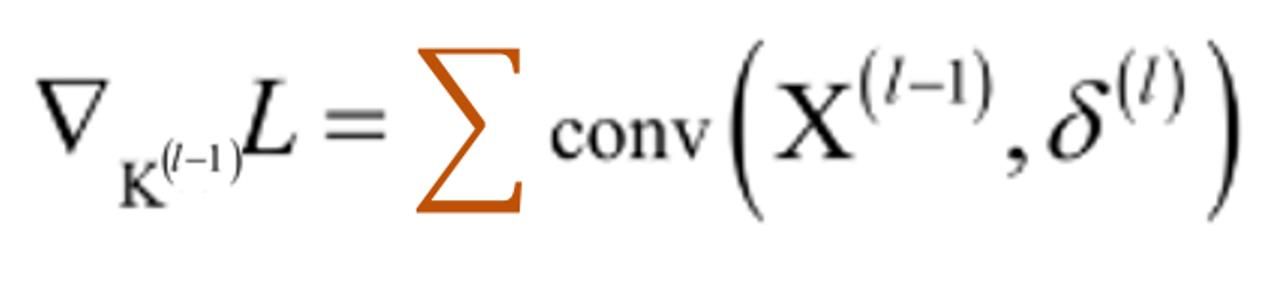
    在这里插入图片描述
    在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/569895.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

java矢量切片实现

java矢量切片实现

概述 可通过多种方式实现矢量切片的制作&#xff0c;前面讲到了基于postgis数据库、tippecanoe、Qgis等方式&#xff0c;本文讲述基于spring Boot框架下java的实现。 实现效果 实现代码 后端代码 引入依赖 <dependency><artifactId>giscat-vector-mvt</art…
阅读更多...
Microsoft Office 2021安装

Microsoft Office 2021安装

哈喽&#xff0c;大家好。今天一起学习的是office2021的安装&#xff0c;有兴趣的小伙伴也可以来一起试试手。 一、测试演示参数 演示操作系统&#xff1a;Windows 11 支持Win10安装&#xff0c;不支持Win7、XP系统 系统类型&#xff1a;64位 演示版本&#xff1a;cn_office_…
阅读更多...
公有云弊端尽显，“云回迁”真的来了吗？

公有云弊端尽显，“云回迁”真的来了吗？

5到10年前&#xff0c;如果一家企业制定数字化转型战略&#xff0c;那么这项战略的核心大概率是将业务迁移上云。 现在&#xff0c;多数企业的业务已在云中“开花结果”&#xff0c;与以往不同的是&#xff0c;原先的一“朵”云变成了一“片”云。 没错&#xff0c;多云战略正…
阅读更多...
Java集合底层原理总结

Java集合底层原理总结

文章目录 一、集合分类二、遍历集合方式三、单列集合3.1 List3.1.1 ArrayList底层分析3.1.2 LinkedList底层分析 3.2 Set3.2.1 HashSet&#xff08;无序&#xff09;底层分析3.2.2 LinkedHashSet&#xff08;有序&#xff0c;存取一致&#xff09;3.2.3 TreeSet&#xff08;可排…
阅读更多...
[LitCTF 2023]easy_shark

[LitCTF 2023]easy_shark

下载附件解压出现密码提示 使用010editor打开&#xff0c;发现frflags和deflags都被修改了&#xff0c;这就会造成压缩包伪加密 将它们都改回0&#xff0c;另存为再打开&#xff0c;不再出现密码提示 使用wirshark打开 过滤http并追踪&#xff0c;在最后一个包里找到了类似fla…
阅读更多...
车载以太网 - SomeIP - 协议用例 - on-wire

车载以太网 - SomeIP - 协议用例 - on-wire

目录 Specification of the SOME/IP on-wire format 1.1、验证Response报文中的源IP地址为Request报文中的目标IP地址
阅读更多...
搭建stm32电机控制代码框架（二）——Stm32CubeMx配置定时器

搭建stm32电机控制代码框架（二）——Stm32CubeMx配置定时器

搭建了基础的环境&#xff0c;配置了一个简单的工程后&#xff0c;CubeMx的基本操作就会了。然后基于这个操作往下推进&#xff0c;开始对关键模块定时器的攻略&#xff0c;这个部分需要先熟悉一下Stm32的定时器基本原理。 《STM32参考手册》中仅对定时器的介绍就已经占了100多…
阅读更多...
C++的最后一道坎 | 百万年薪的程序员

C++的最后一道坎 | 百万年薪的程序员

| 导语 C 的起源可以追溯到 40 年前&#xff0c;但它仍然是当今使用最广泛的编程语言之一&#xff0c;C发明人Bjarne Stroustrup 一开始没想到 C 会获得如此大的成功&#xff0c;他说&#xff1a;“C 的成功显然令人惊讶。我认为它的成功取决于其最初的设计目标&#xff0c;就是…
阅读更多...
用nginx实现一个直播服务—RTMP推流和HTTP-FLV拉流

用nginx实现一个直播服务—RTMP推流和HTTP-FLV拉流

目录 一、环境准备 二、安装编译nginx所需的安装包和下载nginx原代码包 三、nginx配置 四、启动nginx服务 五、测试推流和拉流服务 六、摄像头数据采集 七、查看统计 这篇文章主要记录用nginx实现直播服务&#xff0c;通过RTMP推流和通过HTTP-FLV或RTMP拉流&#xff0c;…
阅读更多...
DJ5-4 链路层交换机

DJ5-4 链路层交换机

目录 一、链路层交换机 二、交换机&#xff1a;支持多节点同时传输 三、交换机&#xff1a;转发表或称交换表 四、交互机&#xff1a;自学习 1. 单个交换机自学习/转发的例子 2. 多个交换机自学习/转发的例子 五、交换机&#xff1a;数据帧的过滤/转发 六、交换机的交换…
阅读更多...
css基础技巧

css基础技巧

1. emmet语法 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title><style>…
阅读更多...
如何在CSDN获取更多的铁粉？

如何在CSDN获取更多的铁粉？

一、铁粉的定义 要想获取铁粉&#xff0c;首先我们得知道什么是铁粉&#xff0c;根据官方给出定义是下面这样的&#xff1a; 【铁粉】具体规则如下&#xff1a; 铁粉 90 天内有阅读&#xff0c;购买专栏或其他互动&#xff0c;并且原力等级 > 0 的粉丝。 也就是说你的原力…
阅读更多...
数据结构——二叉树_(上)

数据结构——二叉树_(上)

学习二叉树之前我们首先要对树有一个认识&#xff0c;树是一种非线性结构&#xff0c;它是由n(n>0)个有限节点组成的一个具有层次关系的节点&#xff1b;而这个层次结构倒过来看就十分的像一棵树&#xff0c;所以起名树结构。 跟现实中的树一样&#xff0c;树结构也有一个根…
阅读更多...
Altium Designer18基础

Altium Designer18基础

原理图 第5课 元件库介绍及电阻容模型的创建.mp4_哔哩哔哩_bilibili 原理图库&#xff08;schLib&#xff09; 1. 创建原理图库&#xff1a; panels -> SCHLIB&#xff1a;左侧弹出SCH Lib窗口 Add&#xff1a;新建原理图库 点击原理图库名称&#xff1a;进入原理图库设置…
阅读更多...
【短视频矩阵系统源码搭建+二开源码定制部署】

【短视频矩阵系统源码搭建+二开源码定制部署】

短视频矩阵源码的框架有很多种&#xff0c;根据不同的业务需求和技术要求&#xff0c;可选择适合的框架。目前常见的短视频矩阵源码框架有&#xff1a;Flutter、React Native、Vue、Angular等前端框架&#xff1b;Spring Boot、Laravel等后端框架&#xff1b;FFmpeg、Pusher、W…
阅读更多...
ChatGPT“保姆级教程”——手把手教你5分钟快速AI智能文字转爆款视频(剪映+百度AIGC平台)

ChatGPT“保姆级教程”——手把手教你5分钟快速AI智能文字转爆款视频(剪映+百度AIGC平台)

目录 前言ChatGPT 剪映ChatGPT生成视频文档安装专业版剪映使用剪映一键出片保姆集教程 百度AIGC平台注册百度AIGC平台使用百度AIGC平台一键出片保姆集教程 总结其它资料下载 前言 在这个数字时代&#xff0c;视频已经成为了最流行的内容形式之一。而如何自动将文字转化为引人…
阅读更多...
JavaScript实现输入学生姓名，按q键程序结束的代码

JavaScript实现输入学生姓名，按q键程序结束的代码

以下为实现输入输入学生姓名&#xff0c;按q键程序结束的程序代码和运行截图 目录 前言 一、输入学生姓名&#xff0c;按q键程序结束 1.1 运行流程及思想 1.2 代码段 1.3 JavaScript语句代码 1.4 运行截图 前言 1.若有选择&#xff0c;您可以在目录里进行快速查找&#…
阅读更多...
Web应用技术(第十三周/第二次练习/7h)

Web应用技术(第十三周/第二次练习/7h)

本次练习基于how2java和课本&#xff0c;学习MyBatis高级映和分页 1.MyBatis高级映射&#xff1a;1.1 相关XML标签及其属性&#xff1a;&#xff08;1&#xff09;mapper标签&#xff1a;&#xff08;2&#xff09;DOCTYPE标签&#xff1a;&#xff08;3&#xff09;typeAliase…
阅读更多...
【MySQL】MySQL体系架构

【MySQL】MySQL体系架构

文章目录 背景一、MySQL体系架构二、网络连接层三、数据库服务层3.1 连接池3.2 系统管理和控制工具3.3 SQL接口3.4 解析树3.5 查询优化器3.6 缓存 四、存储引擎层五、系统文件层5.1 日志文件5.2 数据文件5.3 配置文件5.4 pid文件5.5 socket文件 背景 很多小伙伴工作很长时间了…
阅读更多...
【OJ比赛日历】快周末了，不来一场比赛吗？ #05.27-06.02 #14场

【OJ比赛日历】快周末了，不来一场比赛吗？ #05.27-06.02 #14场

CompHub[1] 实时聚合多平台的数据类(Kaggle、天池…)和OJ类(Leetcode、牛客…&#xff09;比赛。本账号会推送最新的比赛消息&#xff0c;欢迎关注&#xff01; 以下信息仅供参考&#xff0c;以比赛官网为准 目录 2023-05-27&#xff08;周六&#xff09; #8场比赛2023-05-28…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023