✅创作者：陈书予
🎉个人主页：陈书予的个人主页
🍁陈书予的个人社区，欢迎你的加入: 陈书予的社区
🌟专栏地址: Java华为OD机试真题（2022&2023)

1. 题目描述

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为O(log (m+n))。

2. 输入描述

nums1 = [1,3], nums2 = [2]

3. 输出描述

2.00000

4. Java算法源码

public double findMedianSortedArrays(int[] nums1, int[] nums2) {
    int m = nums1.length;
    int n = nums2.length;
    
    // 确保 nums1 的长度小于等于 nums2 的长度
    if (m > n) {
        int[] temp = nums1;
        nums1 = nums2;
        nums2 = temp;
        
        int tempLen = m;
        m = n;
        n = tempLen;
    }
    
    int iMin = 0, iMax = m, halfLen = (m + n + 1) / 2;
    while (iMin <= iMax) {
        int i = (iMin + iMax) / 2;
        int j = halfLen - i;
        
        if (i < iMax && nums2[j - 1] > nums1[i]) {
            iMin = i + 1; // i 太小，增大它
        } else if (i > iMin && nums1[i - 1] > nums2[j]) {
            iMax = i - 1; // i 太大，减小它
        } else { // i 是完美的
            int maxLeft;
            if (i == 0) {
                maxLeft = nums2[j - 1];
            } else if (j == 0) {
                maxLeft = nums1[i - 1];
            } else {
                maxLeft = Math.max(nums1[i - 1], nums2[j - 1]);
            }
            
            if ((m + n) % 2 == 1) {
                return maxLeft;
            }
            
            int minRight;
            if (i == m) {
                minRight = nums2[j];
            } else if (j == n) {
                minRight = nums1[i];
            } else {
                minRight = Math.min(nums1[i], nums2[j]);
            }
            
            return (maxLeft + minRight) / 2.0;
        }
    }
    
    return 0.0;
}

5. 测试

6.解题思路

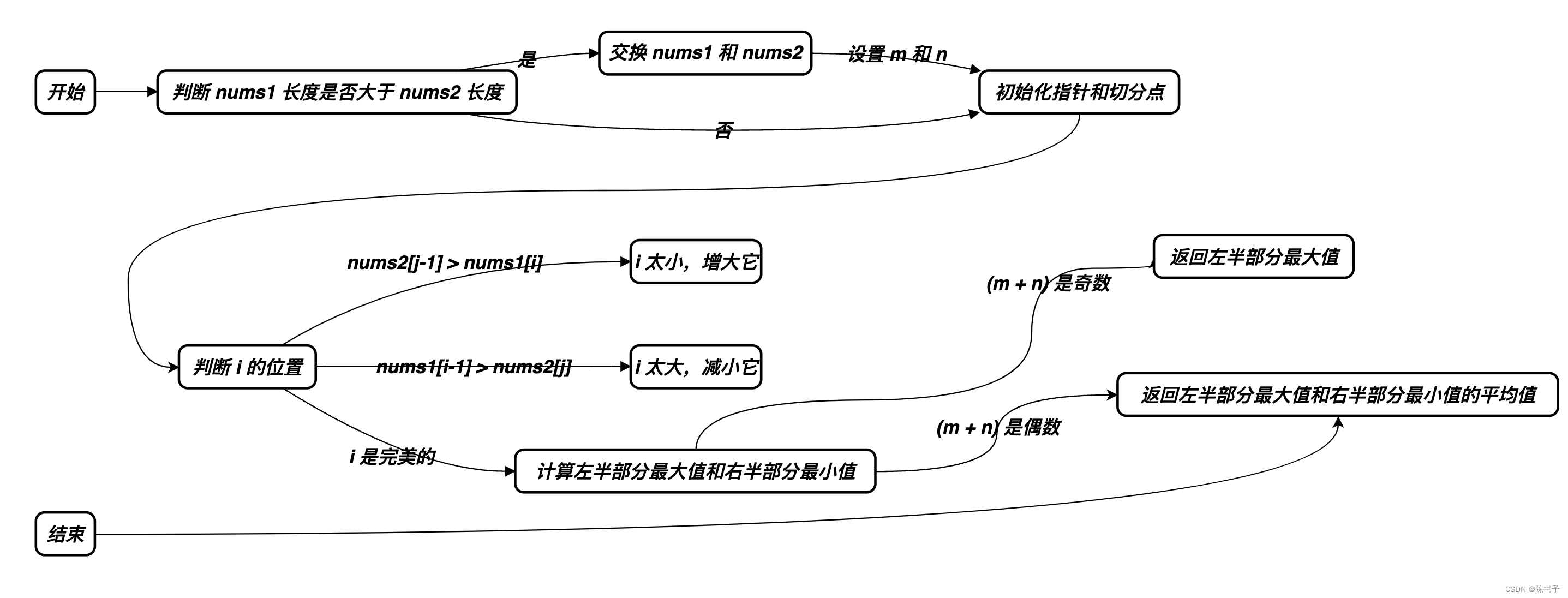
1. 需要确保 nums1 的长度小于等于 nums2 的长度，这样可以保证在进行二分查找时，时间复杂度最低。

2. 定义两个指针 iMin 和 iMax，分别表示在 nums1 中进行二分查找的最小索引和最大索引。初始时，将 iMin 设置为 0，将 iMax 设置为 nums1 的长度。

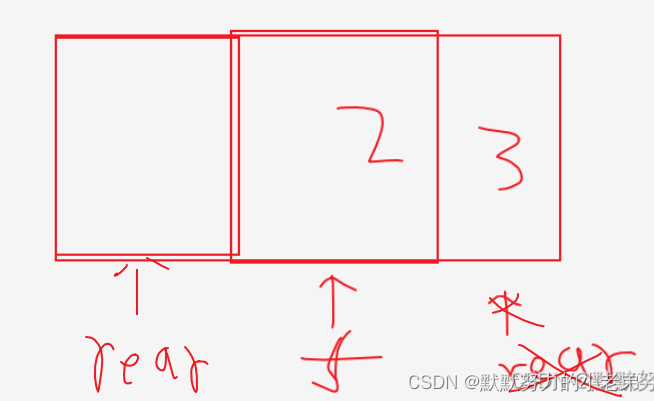
3. 需要计算切分点 i 和 j。切分点 i 表示在 nums1 中的分割点，切分点 j 表示在 nums2 中的分割点。根据 i 和 j 的值，我们可以将两个数组分为左右两部分。

4. 在二分查找的过程中，需要不断调整 i 的值，使得 nums1[i-1] 小于等于 nums2[j]，并且 nums2[j-1] 小于等于 nums1[i]。这样，可以确保左半部分的所有元素都小于等于右半部分的所有元素。

5. 需要根据数组的长度奇偶性来计算中位数。如果 (m + n) 是奇数，中位数就是左半部分的最大值；如果 (m + n) 是偶数，中位数就是左半部分的最大值和右半部分的最小值的平均值。