【模型预测】A-4D战斗机姿态控制的模型预测控制方法（Matlab代码实现）

news2024/9/17 7:33:38

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

飞行器姿态控制通过复杂的动力学来描述，这使得该系统的控制算法的设计变得困难。除此之外，战斗机尤其被设计成天生不稳定的，因为这使它们更加敏捷，能够进行侵略性机动。出于这个原因，需要先进的控制技术来确保飞机的稳定性和控制。目前在飞行器和航天器中，姿态控制的许多研究工作都集中在增量非线性动态反演上。

本文研究了一种应用于A-4D战斗机姿态控制的模型预测控制方法。MPC控制器中使用的动力学模型是飞机旋转动力学的线性化。本文考虑了两种类型的MPC控制，即基于状态的参考跟踪MPC和具有扰动抑制的基于输出的参考追踪MPC，并通过稳定性分析证明了跟踪问题的渐近闭环稳定性。

研究发现，A-4D战斗机的线性化姿态动力学是开环稳定的，无论预测地平线长度如何，都会导致稳定性。此外，还发现A-4D战斗机在跟踪特定俯仰角时能够抑制干扰。

📚2 运行结果

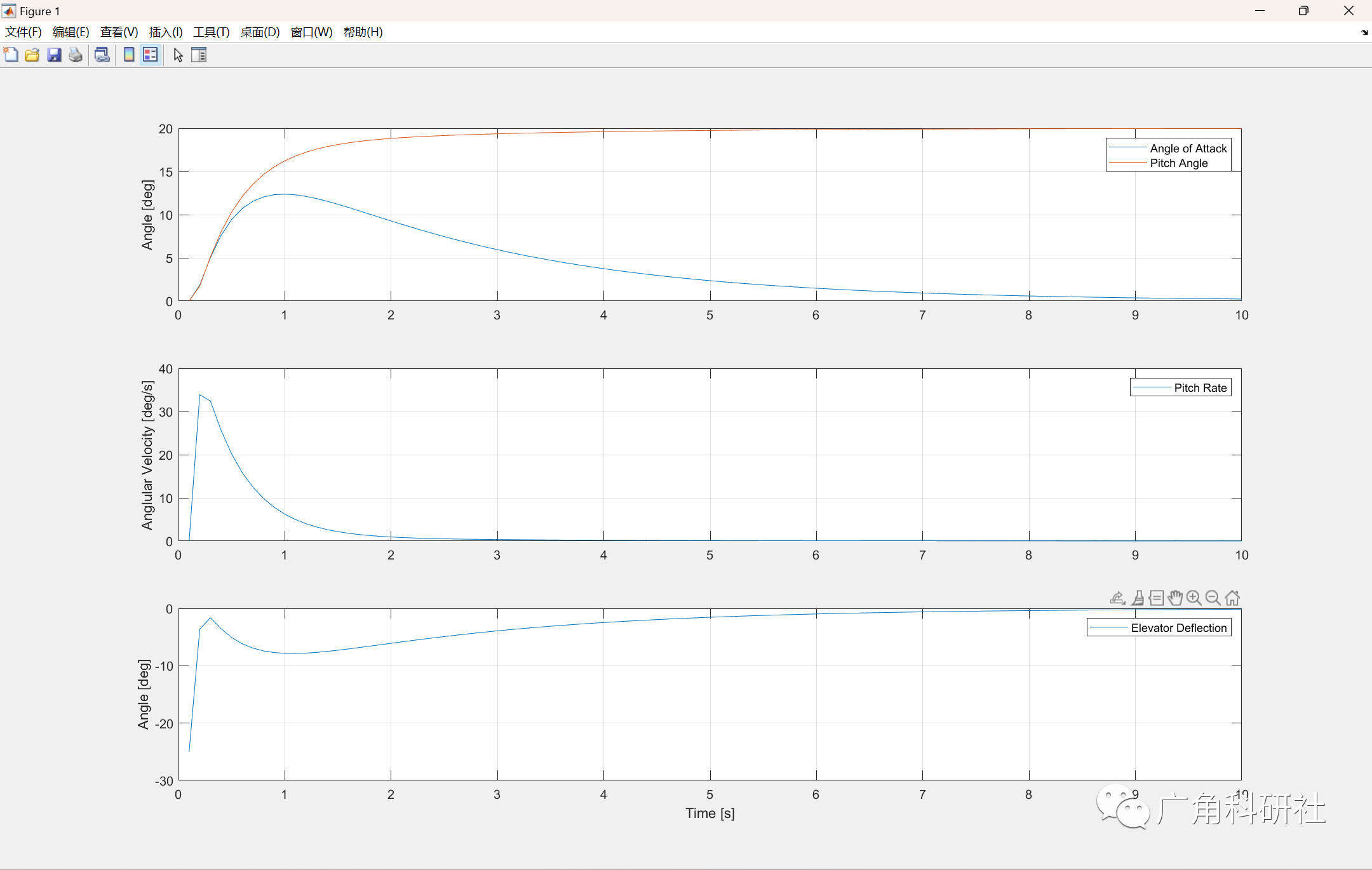
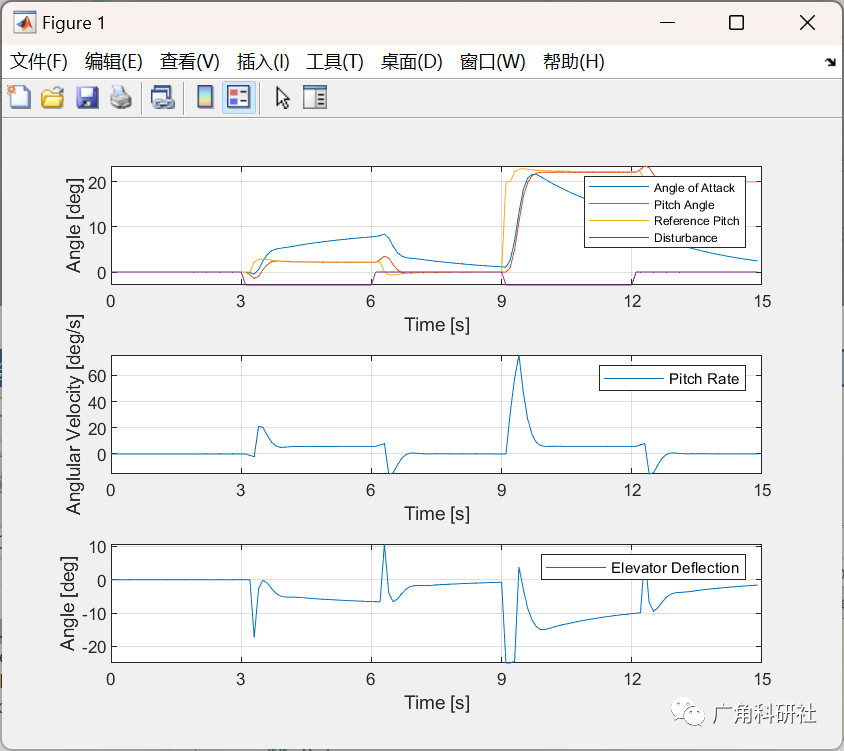
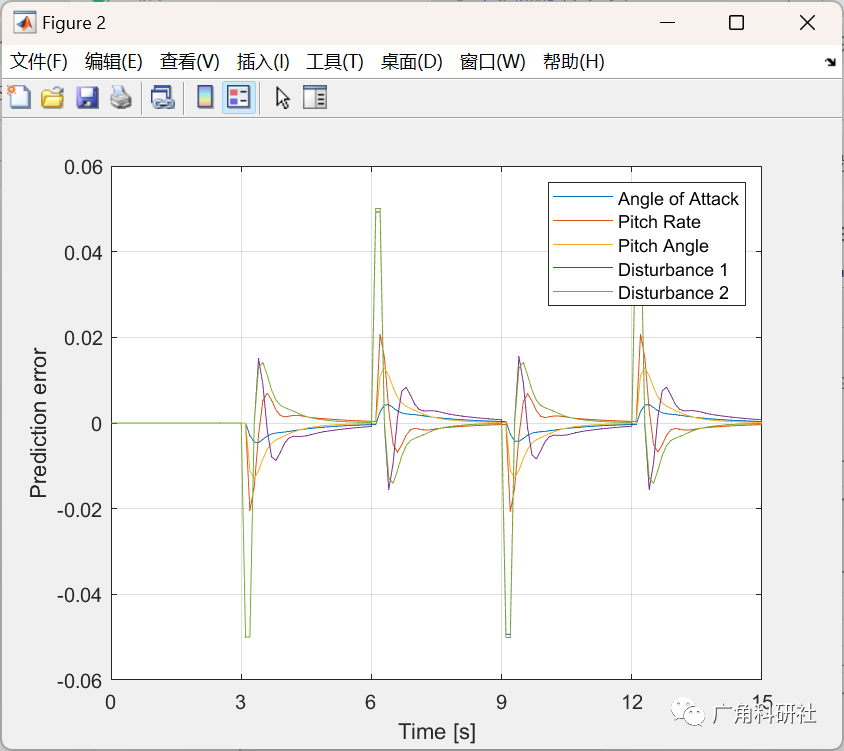
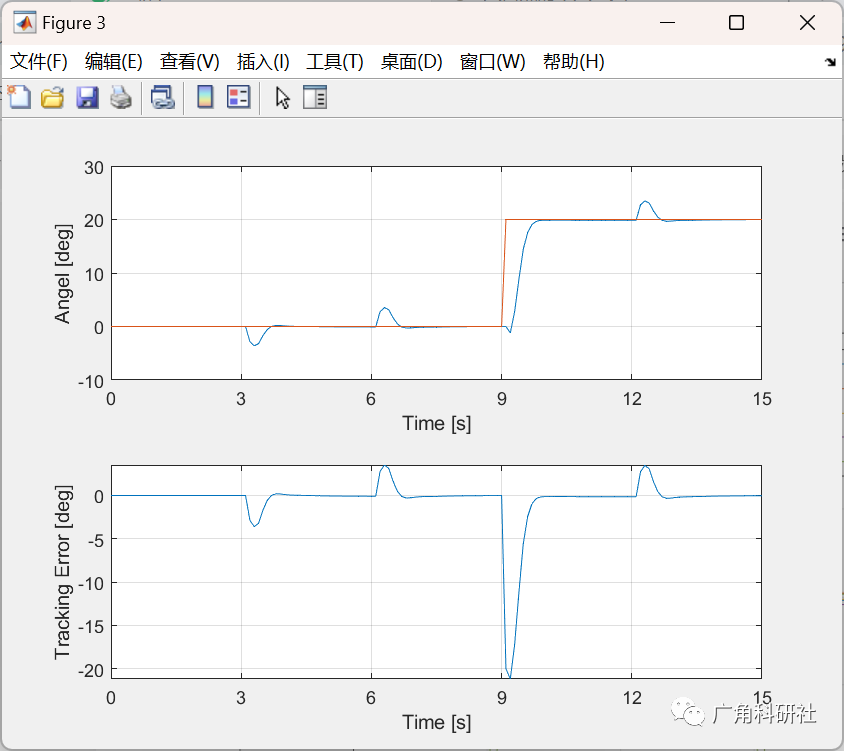
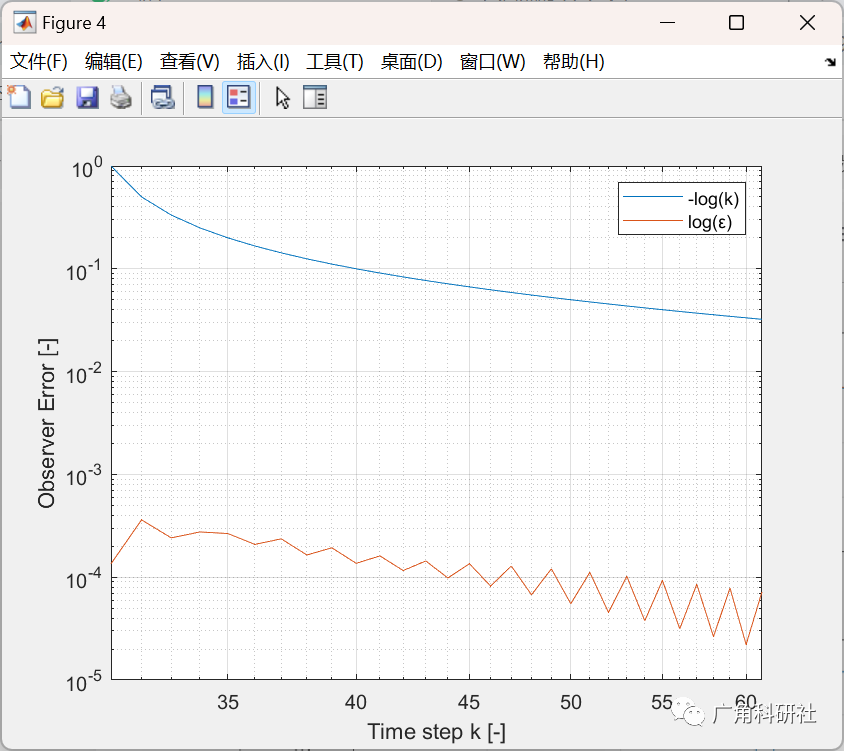
主函数部分代码：

clear all
clc
close all

%% Data

% states = [angle of attack, pitch rate, pitch angle]

dt = 0.1;    %time step
T=15;        %simulation time
Nsim = T/dt; %number of simulation steps

%Continuous-time model dynamics

A = [ -0.5507  1      0;
      -9.7621 -0.9983 0;
       0       1      0 ];              
B = [ -0.0545
      -14.494
      0 ];               
C = [ 0 1 0;
      0 0 1 ];
D = [ 0;  0 ];

%Discrete-time model dynamics

sys = ss(A, B, C, D);                       %state-space model
sys = c2d(sys, dt);                         %discrete state-space model

%LTI system definition

LTI.A = sys.A;

LTI.B = sys.B;

LTI.C = sys.C;

LTI.D = sys.D;
              
LTI.x0 = [ 0.0; 0; 0.0 ];
LTI.d = [ 0.0; 0.0 ];
LTI.yref = [ 0.0; 0.0 ];

%Definition of system dimension

dim.nx = 3;     %state dimension
dim.nu = 1;     %input dimension
dim.ny = 2;     %output dimension
dim.nd = 2;     %disturbance dimension
dim.N =  5;     %horizon

%Definition of quadratic cost function

weight.Q = diag([10, 10, 500]);                  %weight on output
weight.R = eye(dim.nu);                          %weight on input
weight.P = dare(sys.A,sys.B,weight.Q,weight.R);  %terminal cost

%% Observer gain and disturbance matrices

K = place(LTI.A',(LTI.C*LTI.A)',[0.85; 0.90; 0.55])';      %tuning gain matrix
L = [K; eye(2)];                                           %observer gain
LTI.Bd = K;
LTI.Cd = eye(2) - C*K;

%% Check observability condition

rank = rank([eye(dim.nx)-LTI.A -LTI.Bd; LTI.C LTI.Cd]);
disp(rank)

%% Augmented system dynamics

LTIe.A = [ LTI.A LTI.Bd; zeros(dim.nd,dim.nx) eye(dim.nd) ];
LTIe.B = [ LTI.B; zeros(dim.nd,dim.nu) ];
LTIe.C = [ LTI.C LTI.Cd ];
LTIe.x0 = [ LTI.x0; LTI.d ];
LTIe.yref = LTI.yref;

%Definition of system dimension
dime.nx = 5;     %state dimension
dime.nu = 1;     %input dimension
dime.ny = 2;     %output dimension
dime.N  = dim.N; %horizon

%Definition of quadratic cost function
weighte.Q = blkdiag(weight.Q, zeros(dim.nd));            %weight on output
weighte.R = weight.R;                                    %weight on input
weighte.P = blkdiag(weight.P, zeros(dim.nd));            %terminal cost