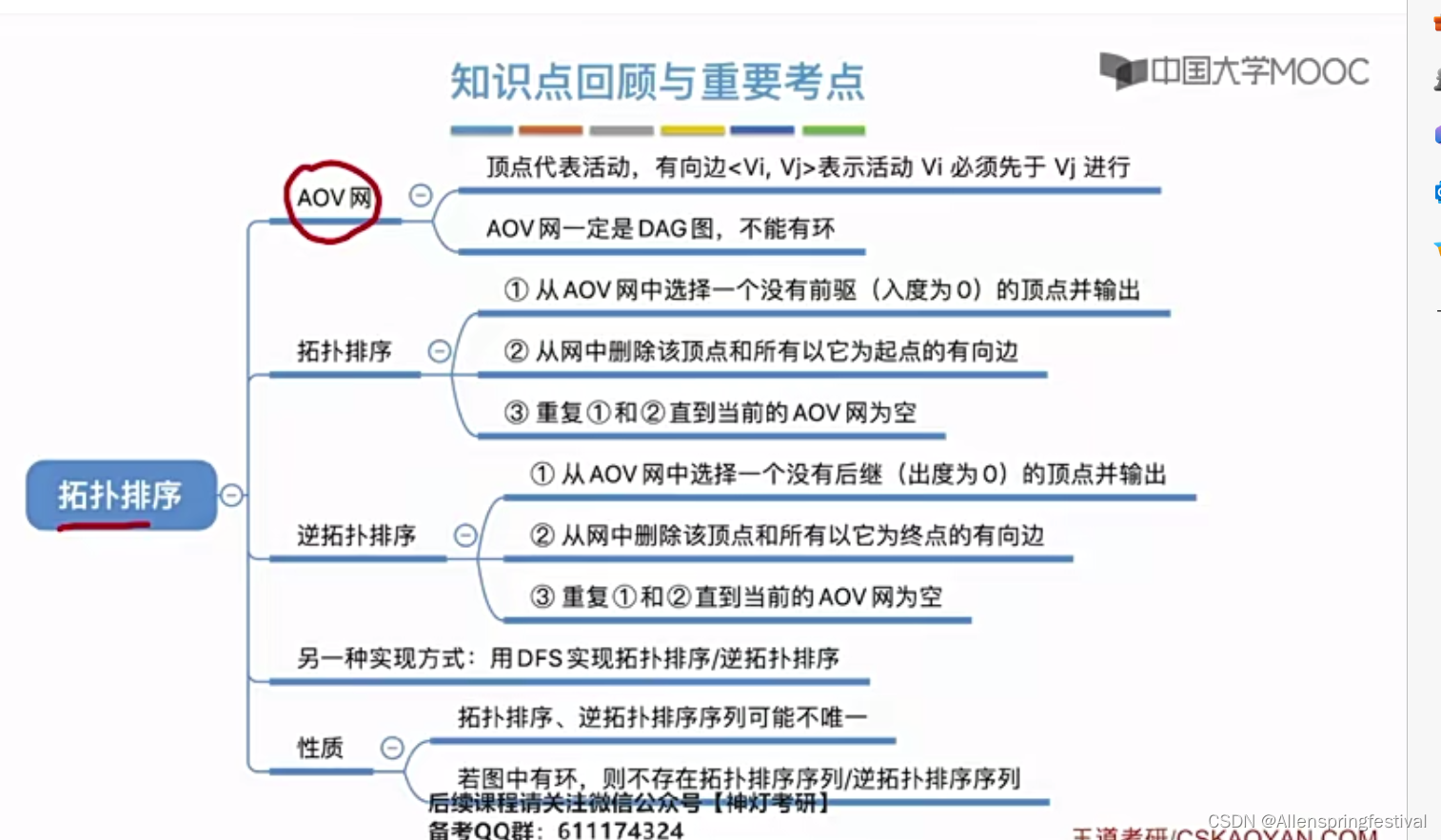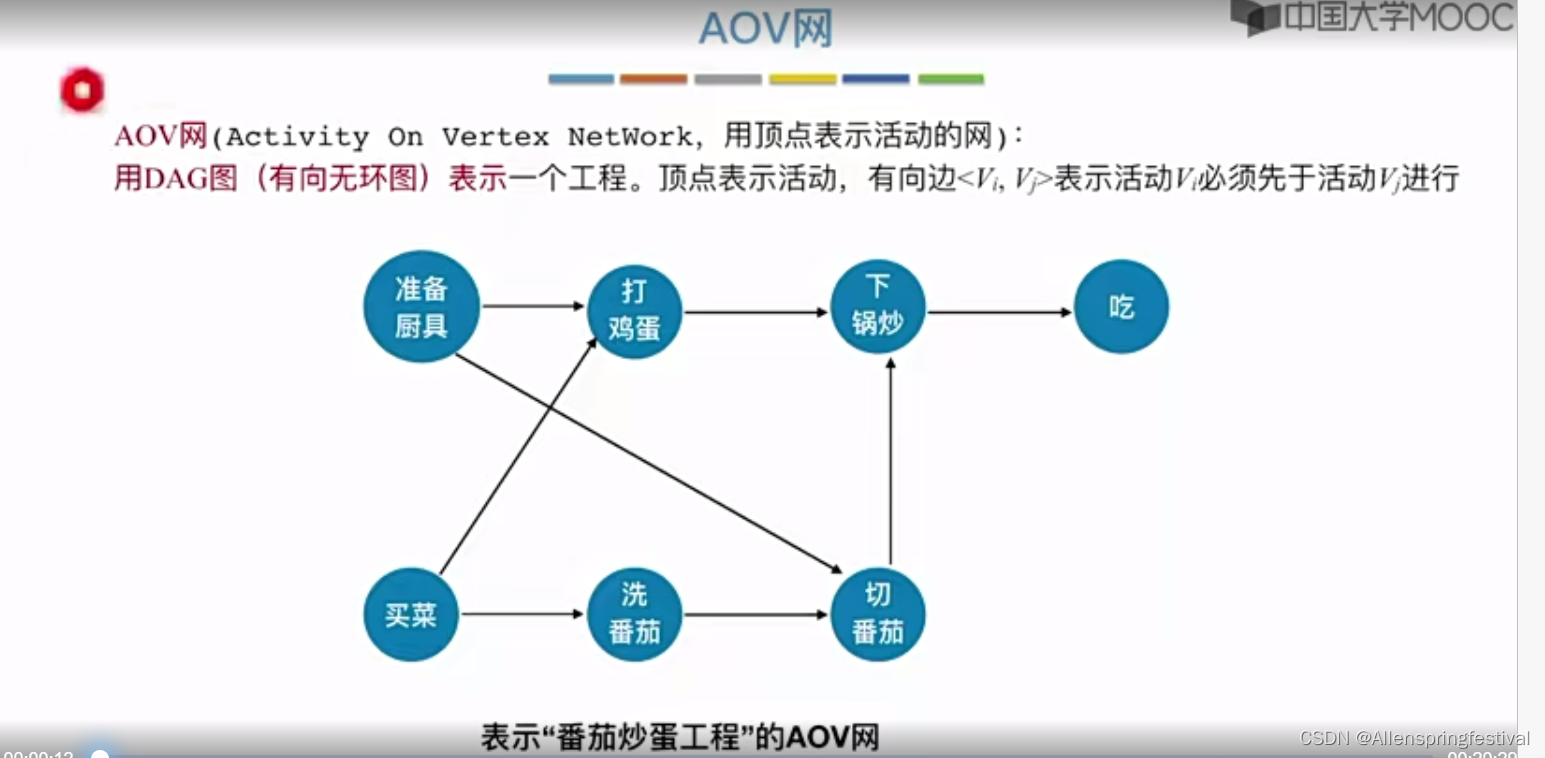
用DAG（有向无环图）表示一个工程。顶点表示活动，有向边<Vi，Vj>表示活动Vi活动必须先与Vj活动进行。

 所谓的拓扑排序：找到做事的先后顺序

 

 

 

 

 

 

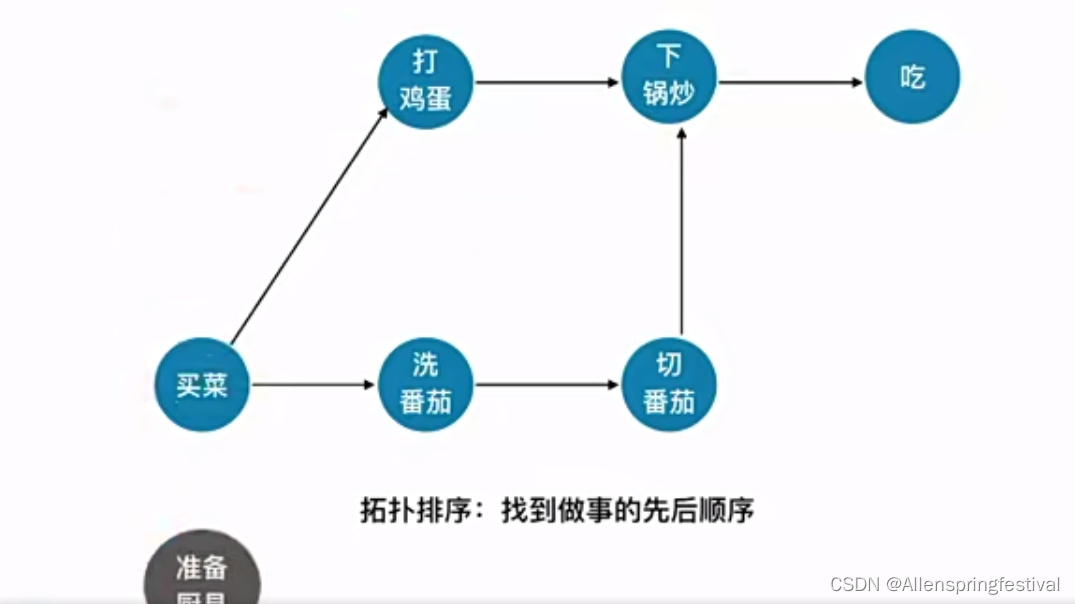
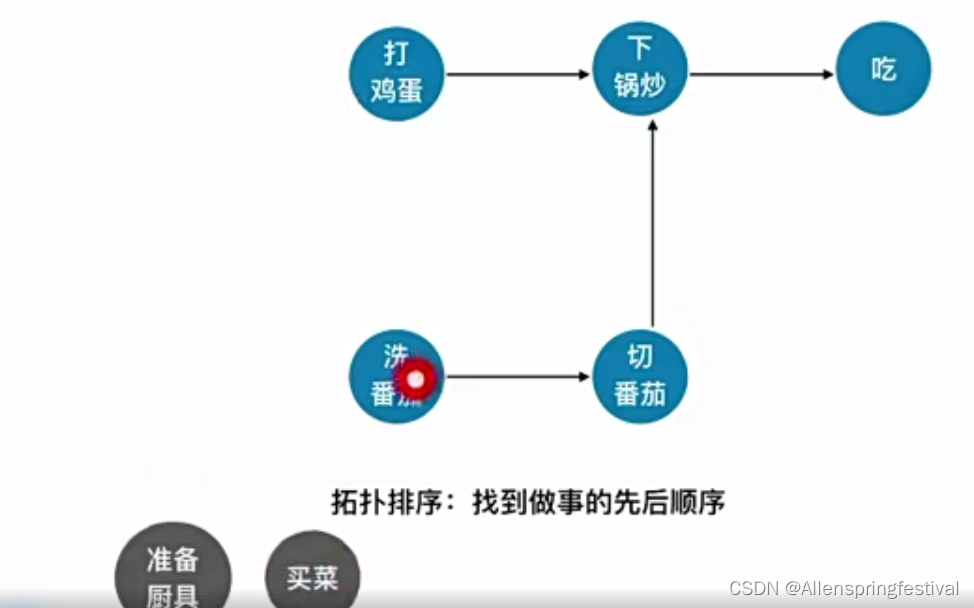
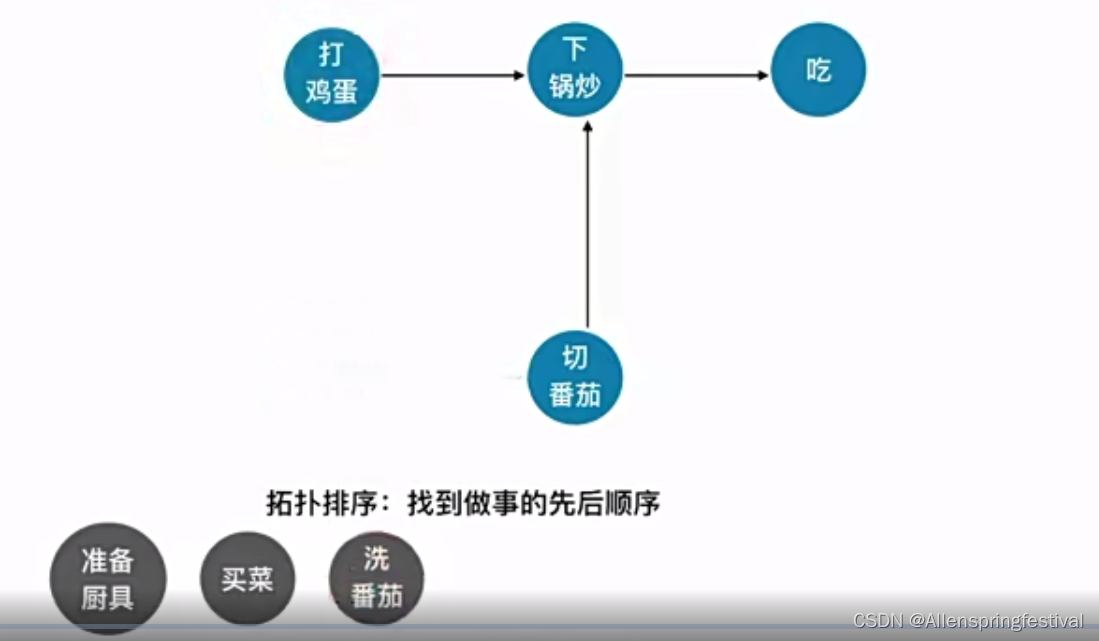
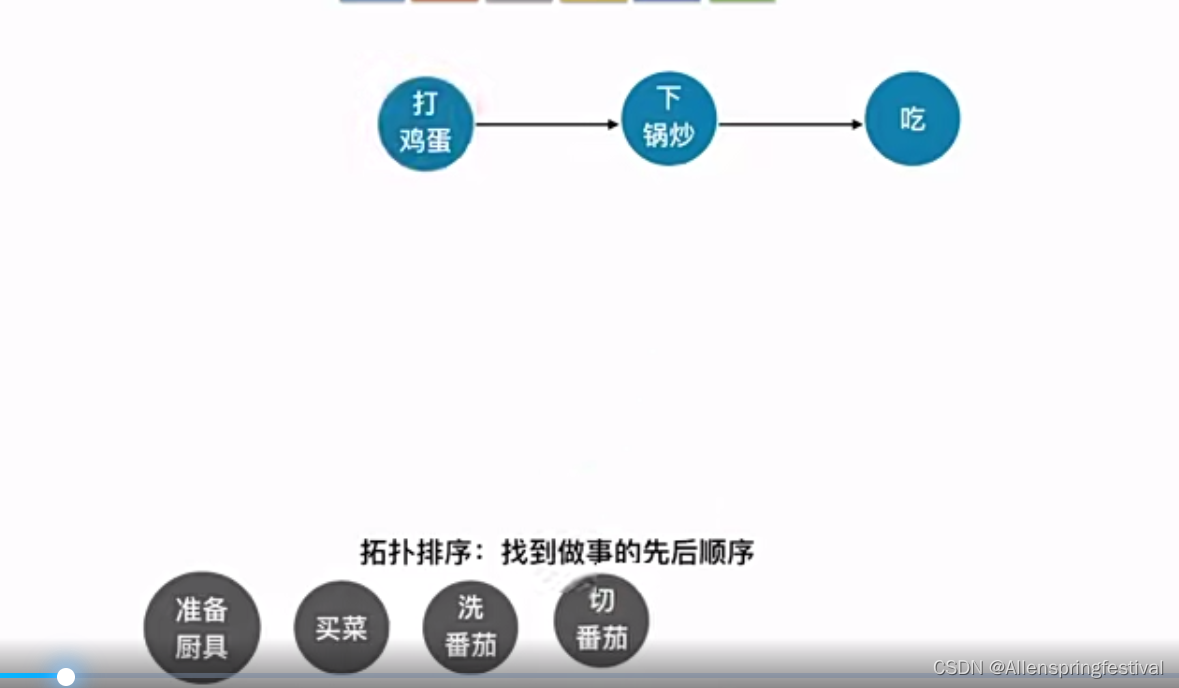
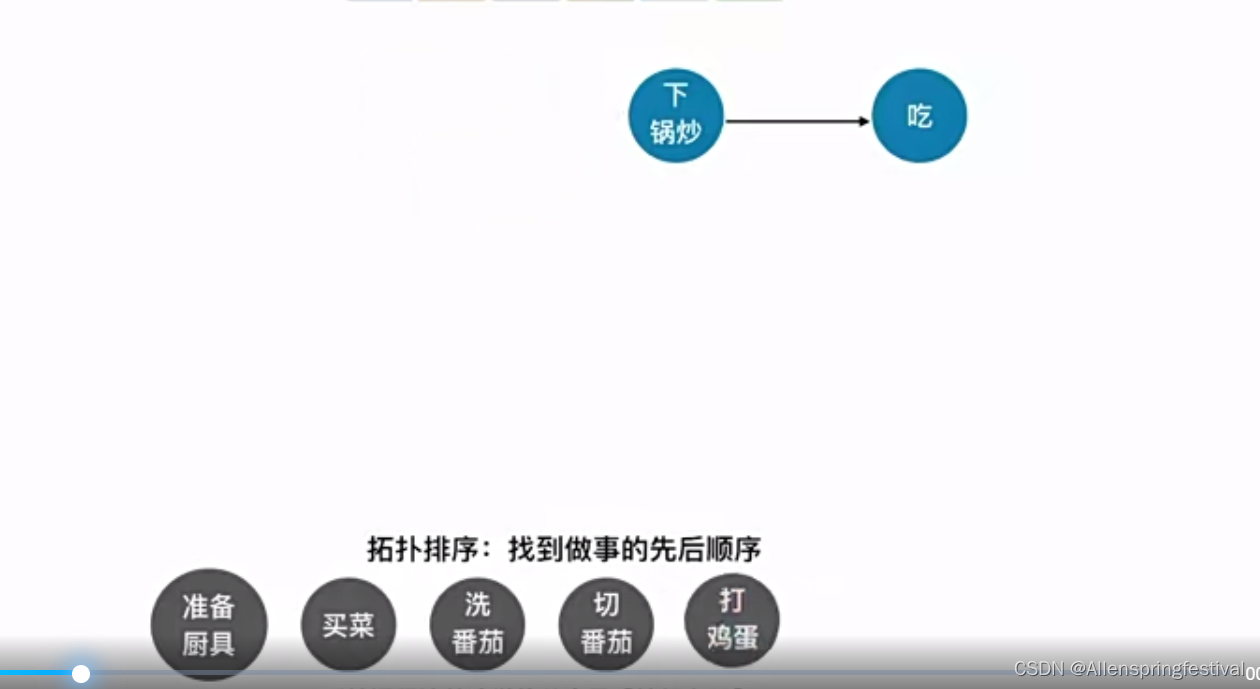
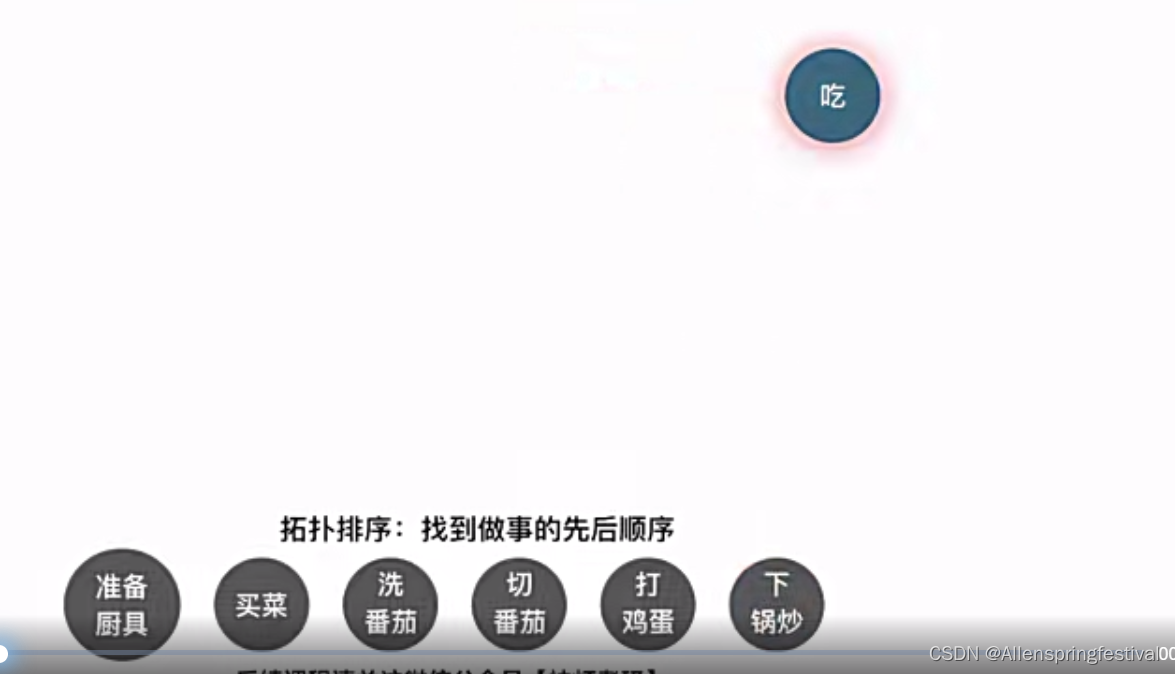
以上根据拓扑排序的实现：

加入对有回路的图进行拓扑排序：

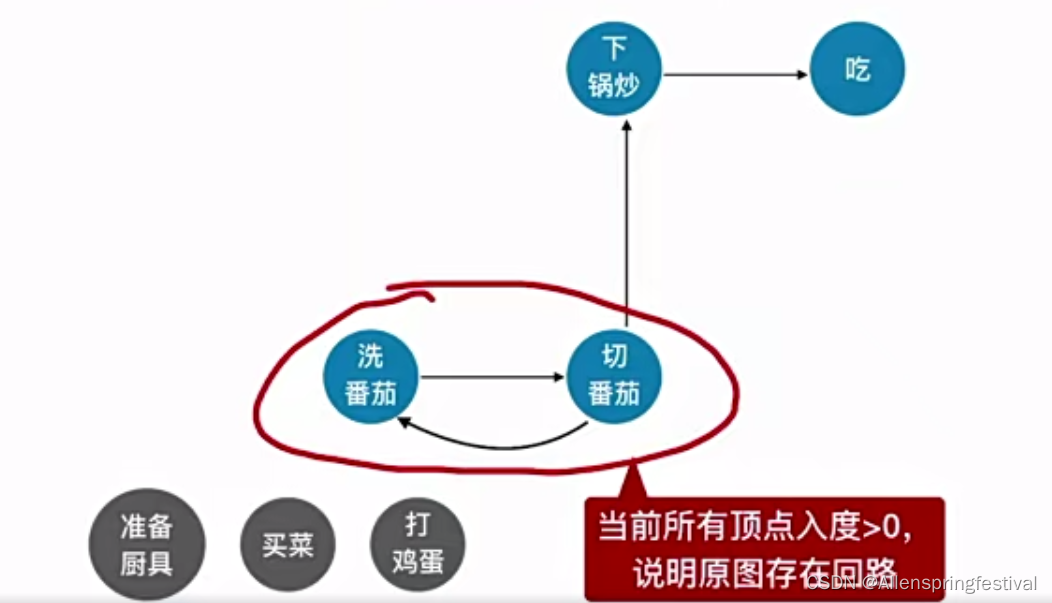
 所以原图如果存在回路，就不存在拓扑排序。

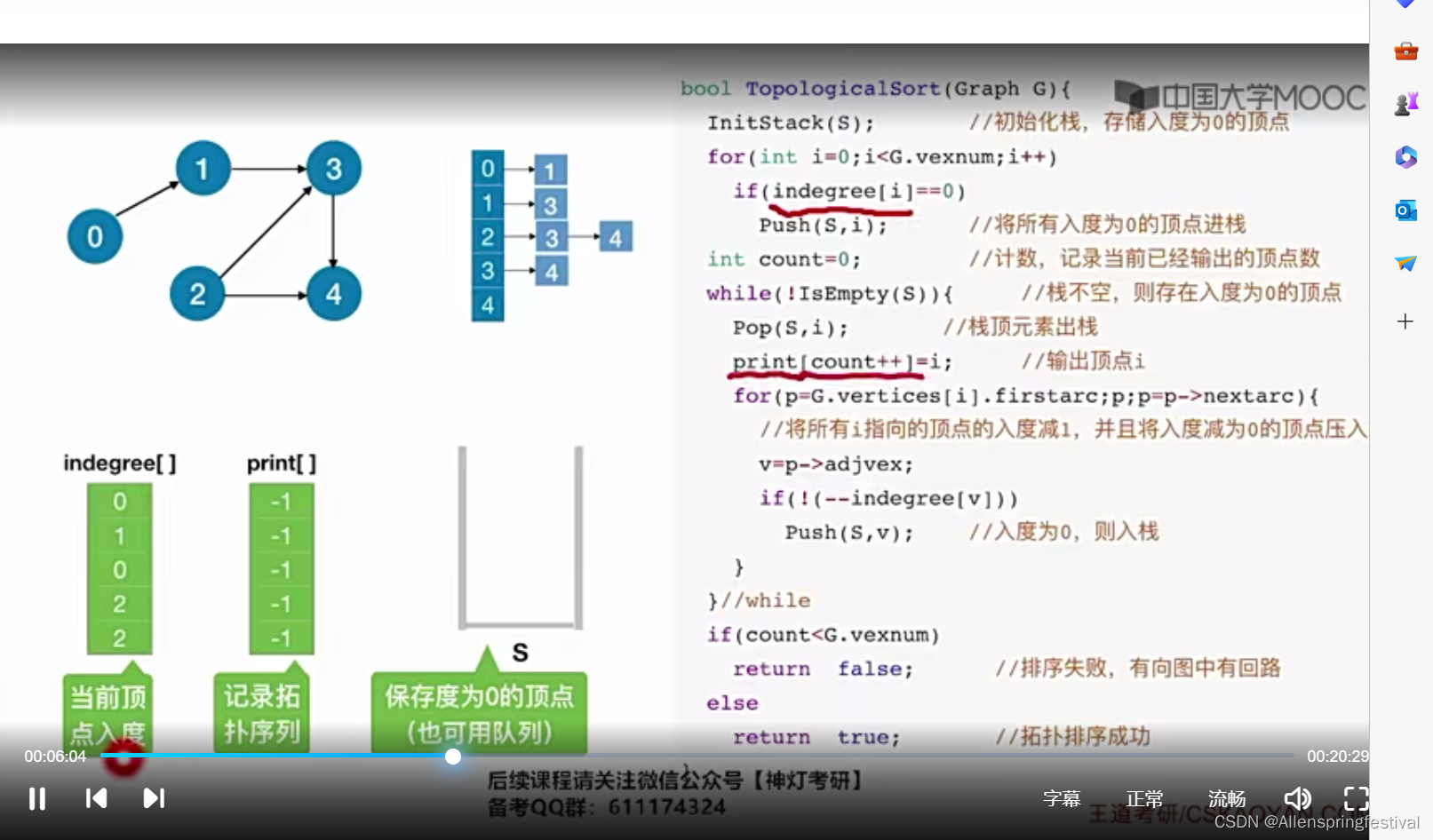
 采用邻接表进行存储

定义了一个indegree[]数组

定义一个print数组（刚开始全部初始化为-1）

一个空栈S

 

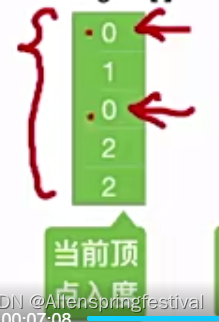
 检查indegree数组当前入度为0的顶点

 

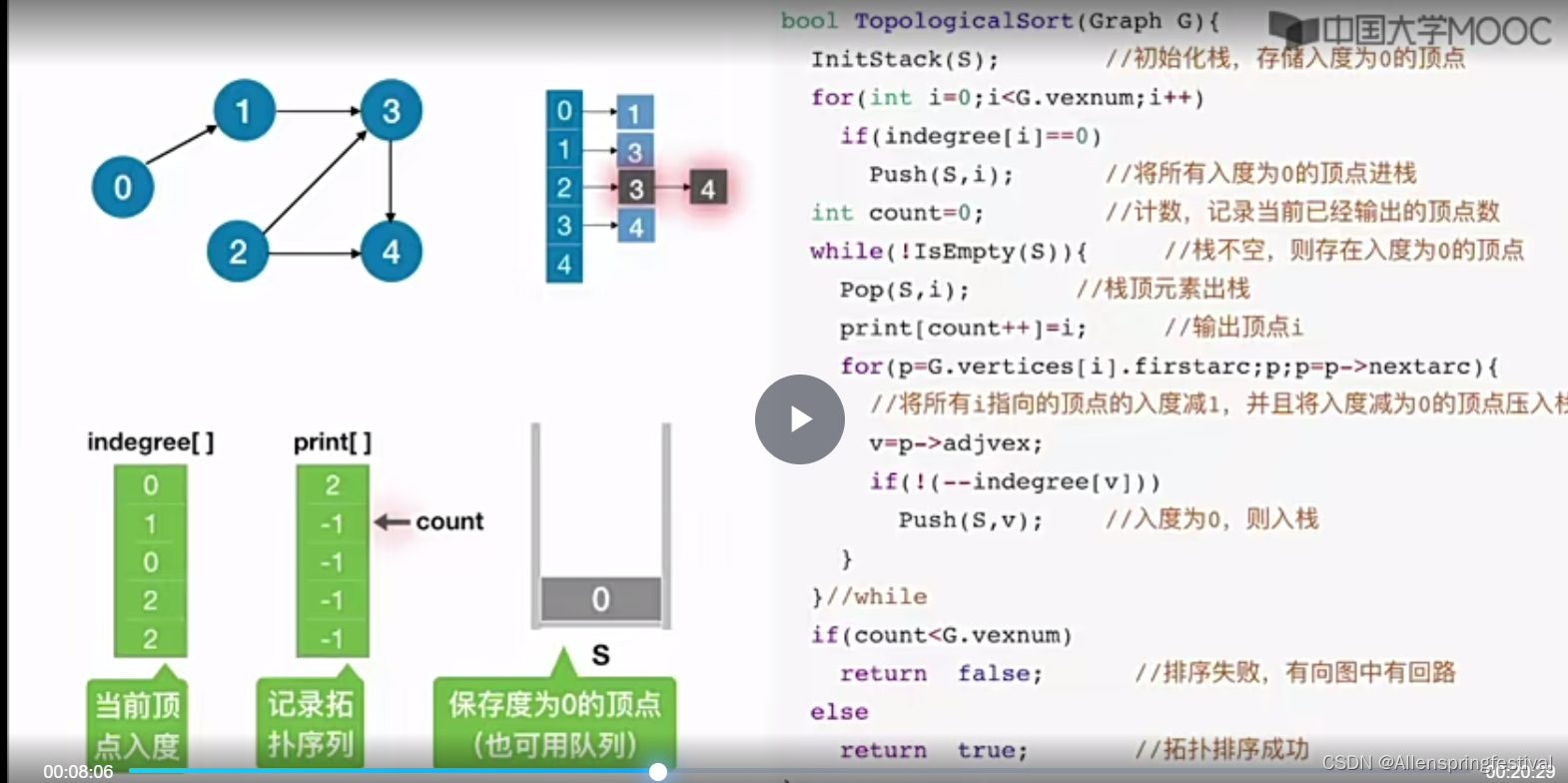
将与2号结点相连的结点的入度减去1.

 

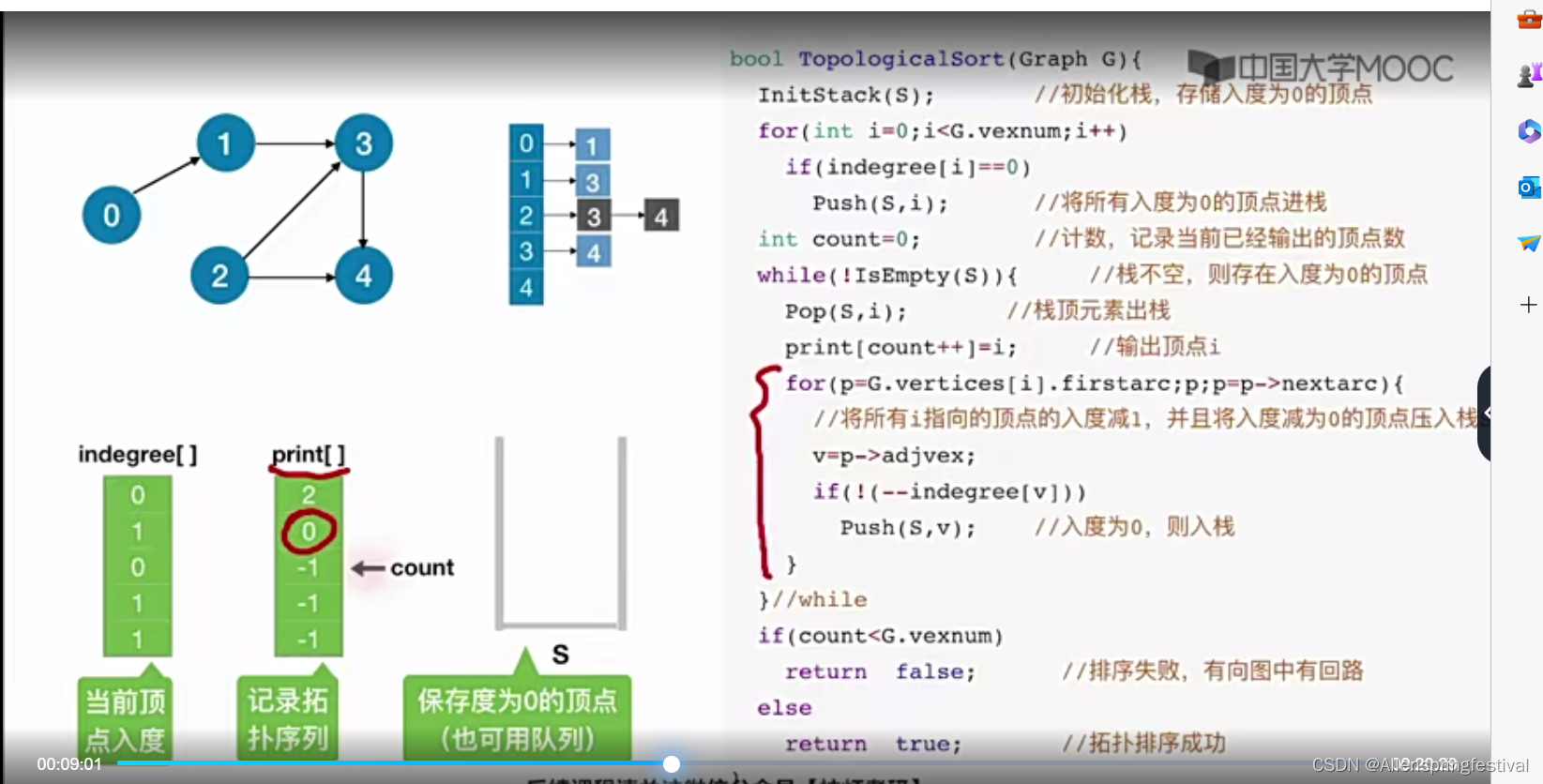
 接下来我们处理入度为0的还有0号结点。

在while循环里面处理和0号结点相连的几个节点。

接着是1号结点的入度因为减去1之后变成了0。

 此时将1号结点也压入栈中

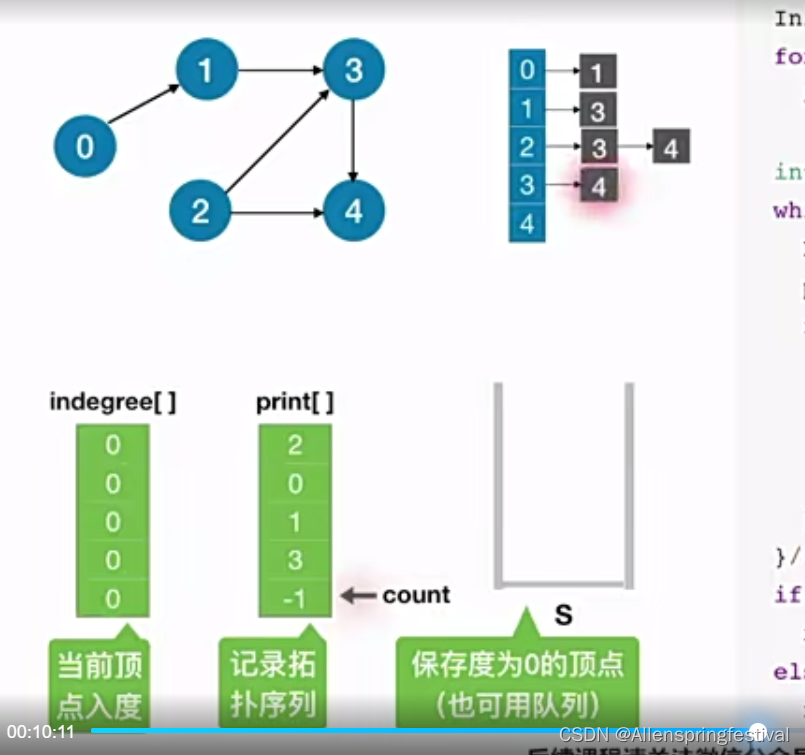
 接着把3号结点和4号结点也压入栈中。

 

下面我们来认识一下逆拓扑排序：

出栈的时候出出度为0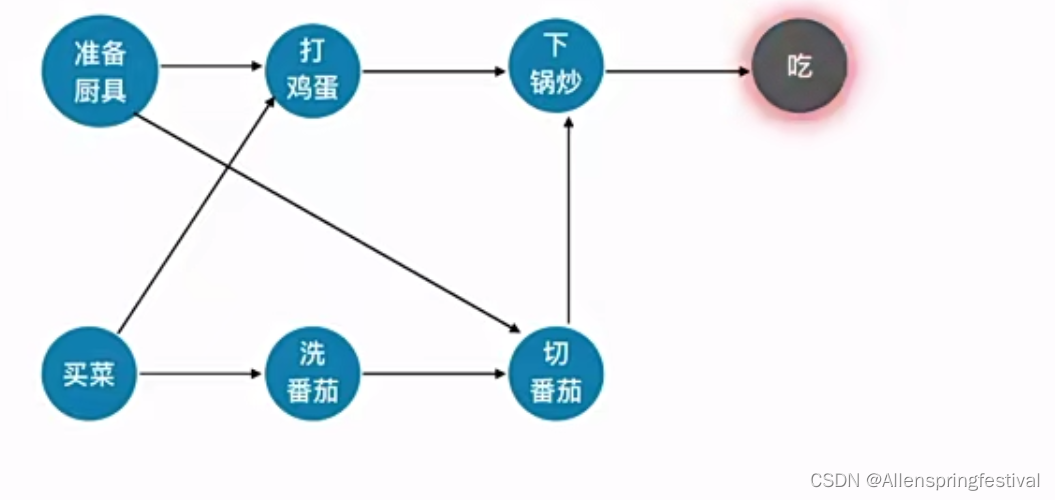

 

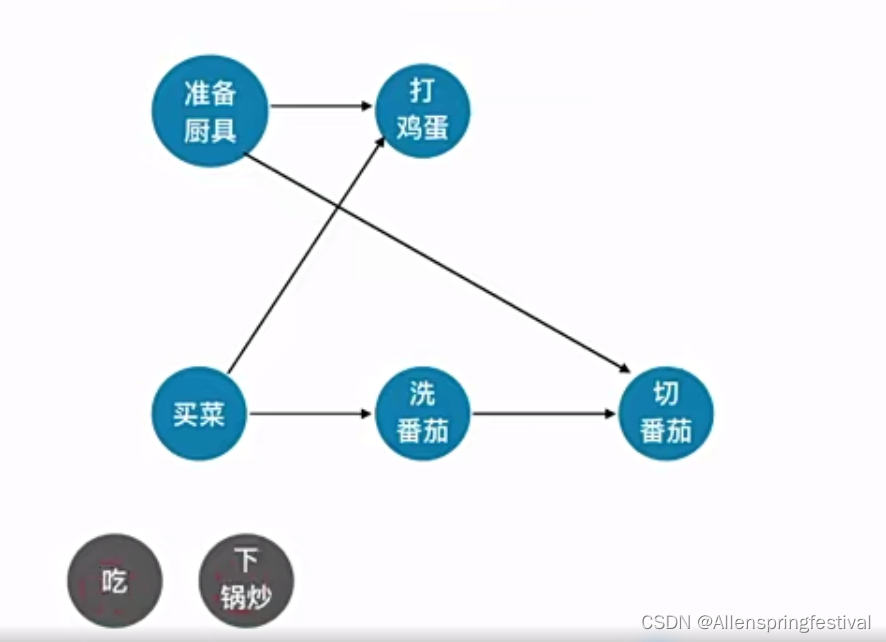
 随便删除切番茄和打鸡蛋

 

 

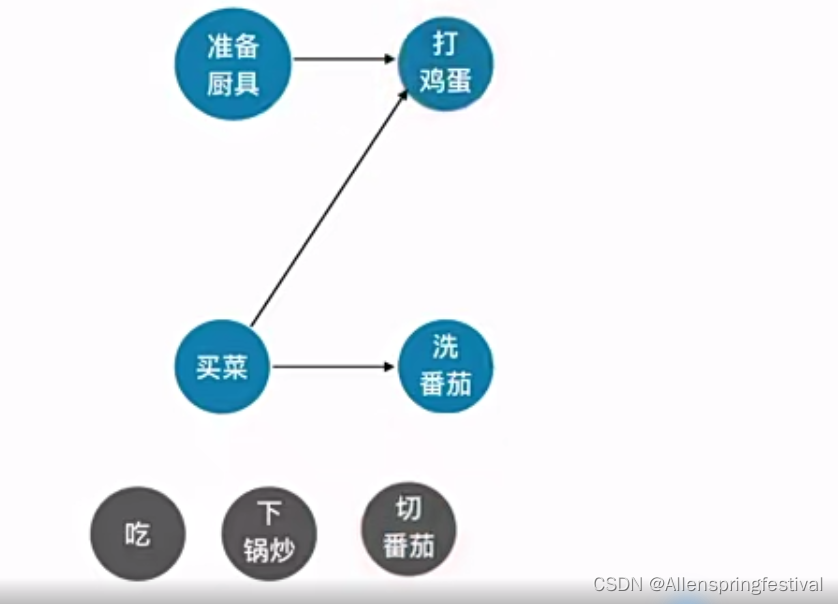
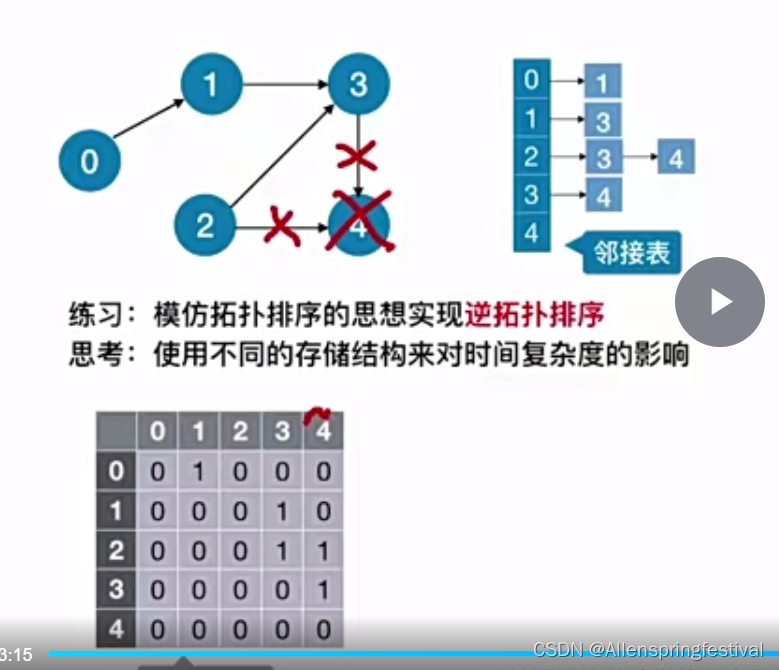
 我么在删除出度为0的顶点时，还需要删除对应的边，就需要将邻接表全部遍历一遍去寻找其前驱。

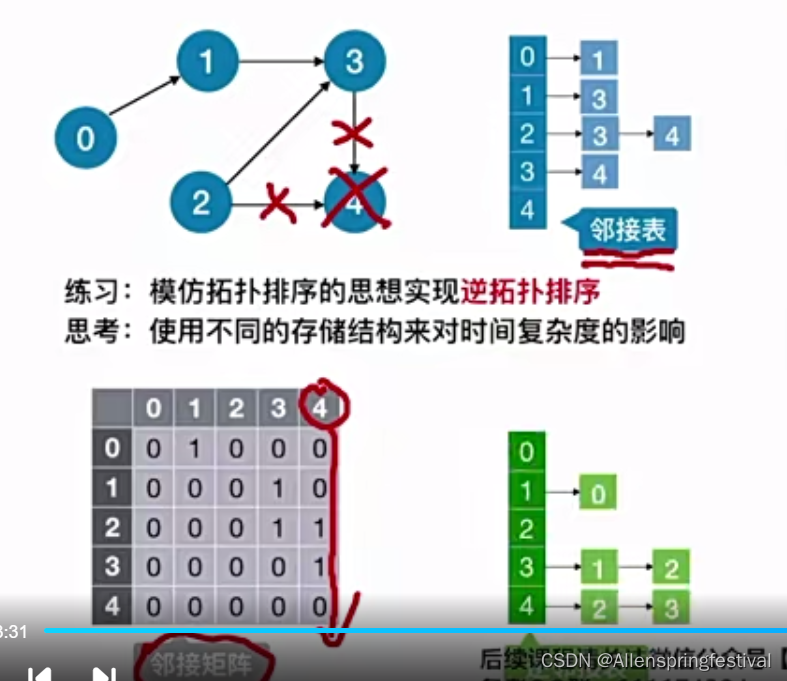
 所以最好使用邻接矩阵去存储（这样就可以直接去第5列的值）

发现它的前驱是2和3.

也可以采用逆邻接表去存储

我们也可以用DFS算法实现拓扑排序

 

 

 

 

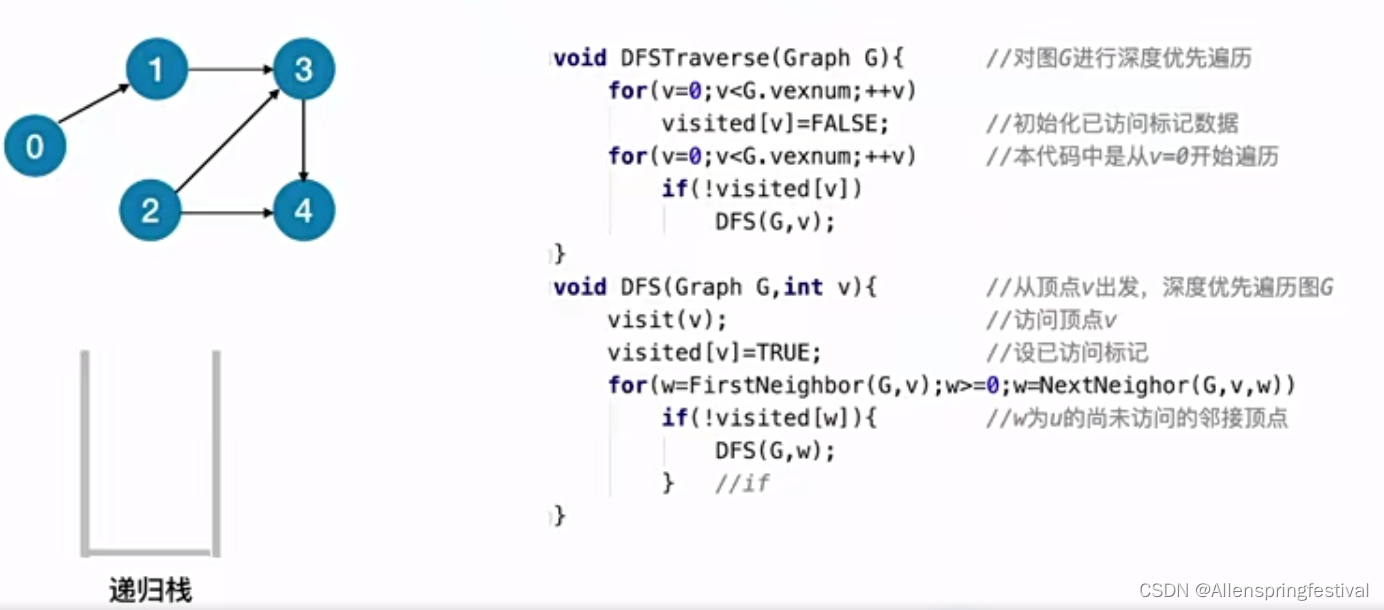
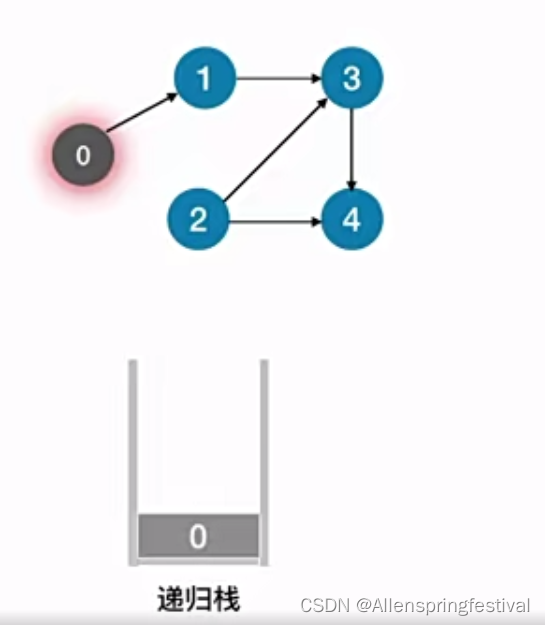
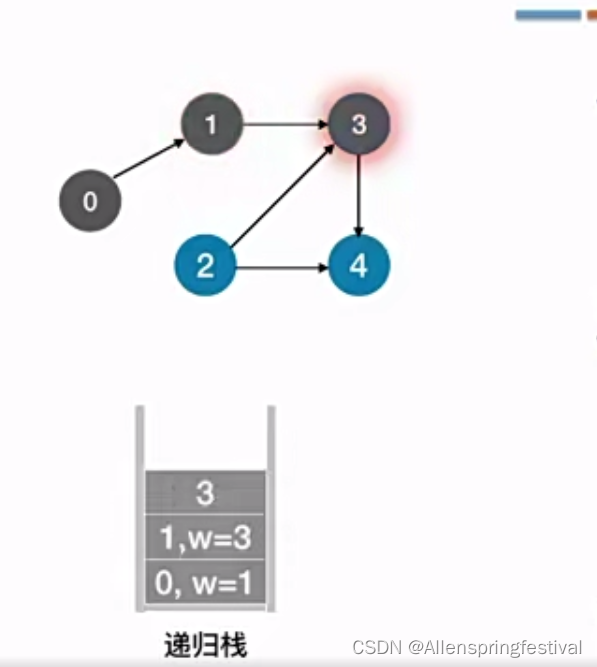
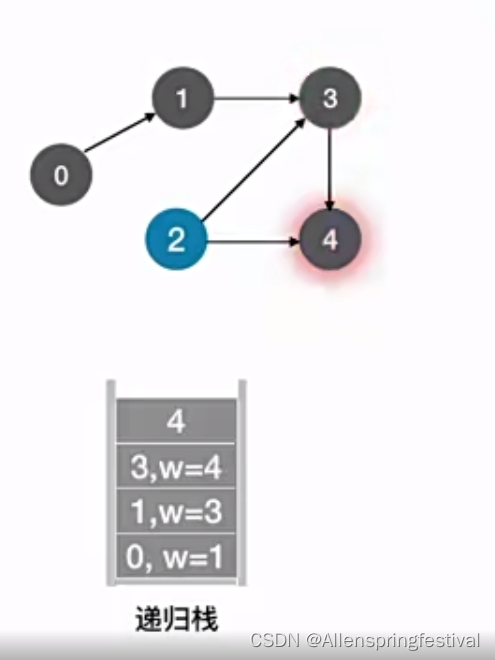
 接下来我们会把4打印输出：

 对于3号节点来说，也找不到一个与之相邻且未被访问过的结点。

 

 

 

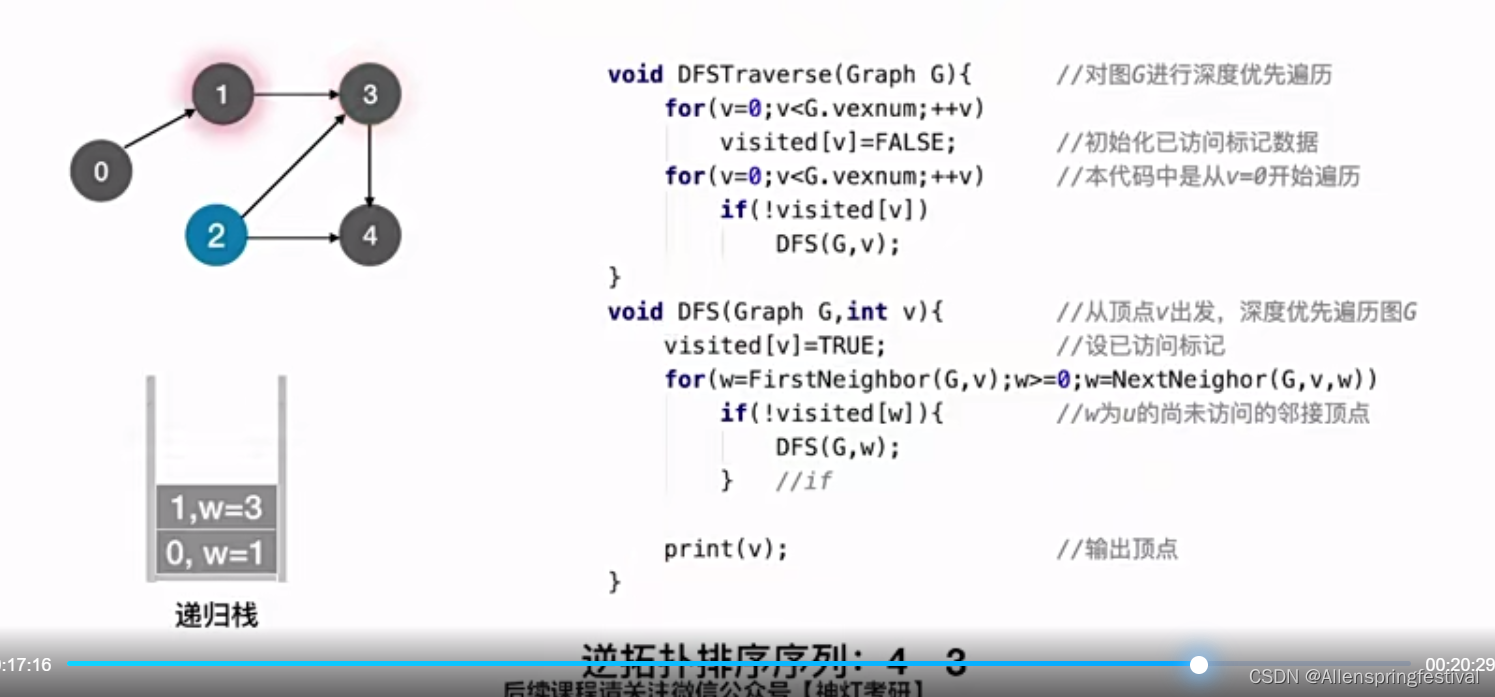
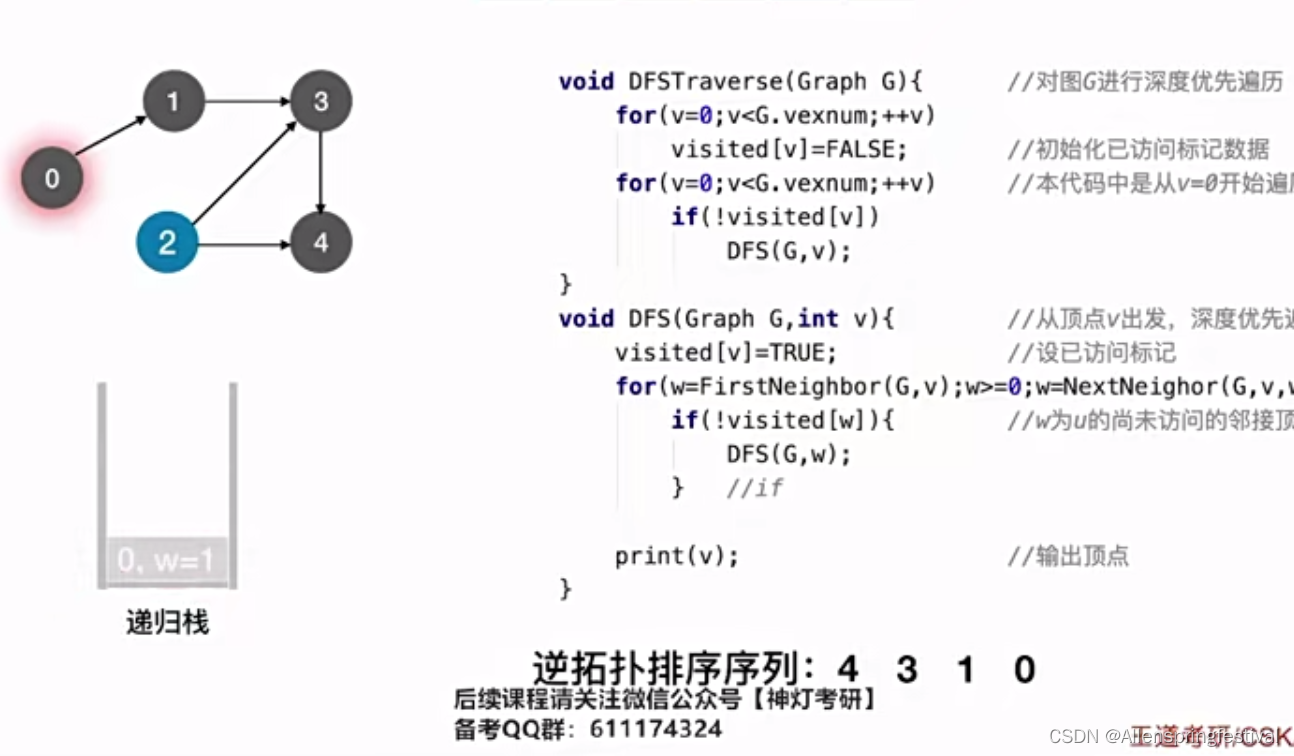
 我们的函数会重新回到上面这个for循环，寻找visited数组为False的顶点。

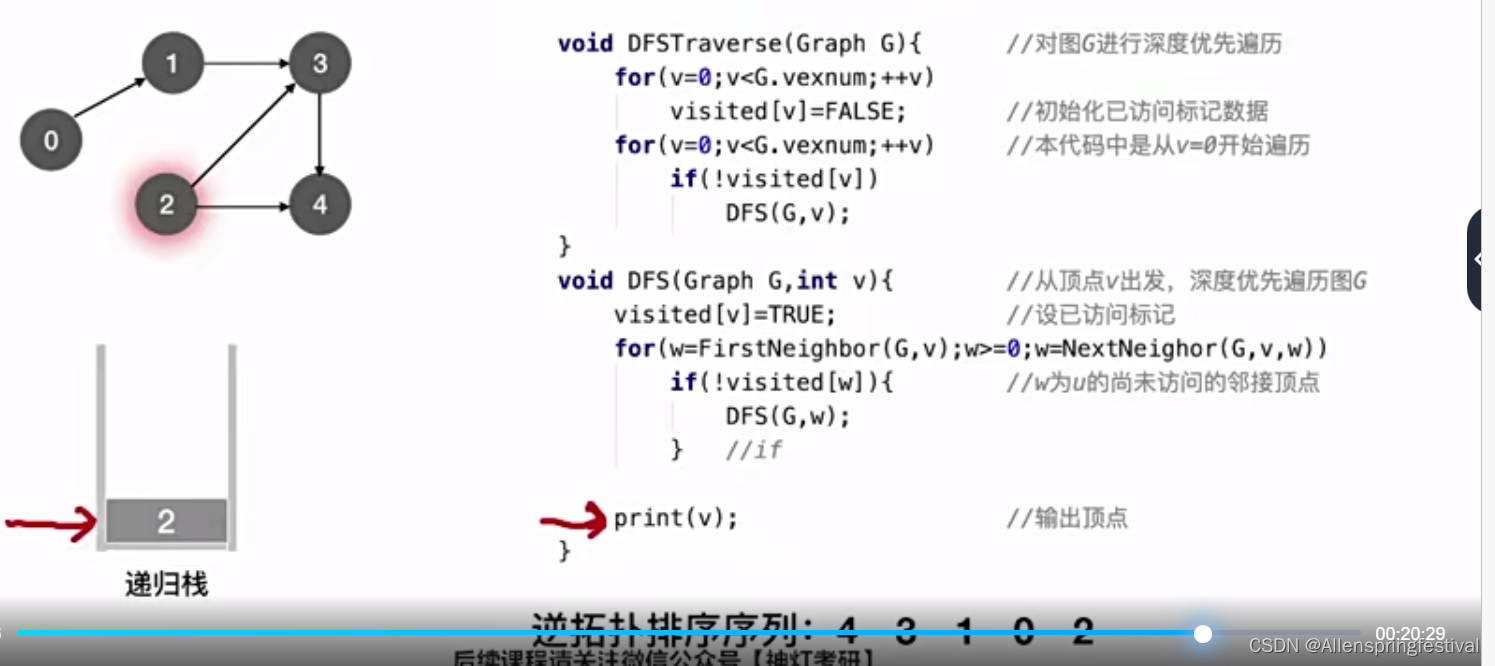
 随意我们发现使用DFS算法，顶点在推出递归栈之前会输出成逆拓扑排序失败