DR2: Diffusion-based Robust Degradation Remover for Blind Face Restoration (Paper reading)

Zhixin Wang, Shanghai Jiao Tong University, CH, CVPR2023, Cited:0, Code, Paper

1. 前言

传统的盲脸部修复通常使用预定义的退化模型来合成降质的低质量数据进行训练，而实际世界中可能出现更复杂的情况。假设的退化模型与实际情况之间的差距会影响修复效果，输出结果中经常出现伪影。然而，为了覆盖实际情况，将每种类型的退化都包含在训练数据中是昂贵且不可行的。为了解决这个鲁棒性问题，我们提出了基于扩散的鲁棒退化去除器（DR2），首先将退化图像转化为粗糙但退化不变的预测，然后利用增强模块将粗糙预测恢复为高质量图像。通过利用表现良好的去噪扩散概率模型，我们的DR2将输入图像扩散到带有高斯噪声的噪声状态，各种类型的退化转化为高斯噪声，然后通过迭代去噪步骤捕捉语义信息。因此，DR2对常见的退化（例如模糊、调整大小、噪声和压缩）具有鲁棒性，并且与不同设计的增强模块兼容。在各种设置下的实验证明，我们的框架在严重退化的合成和实际世界数据集上优于最先进的方法。

2. 整体思想

ILVR的采样效果一般，本文算是对其方法的改进。先说结果，我测试感觉结果非常一般，创新型也一般，Git上没人关注，不知道为什么能发CVPR，运气运气。整体思想就是控制去噪的步数做个截断，然后对估计出的图像（很平滑）使用一个增强网络增强。

3. 方法

整体盲脸部修复框架DR2E由基于扩散的鲁棒退化去除器（DR2）和增强模块（E）组成。在第一阶段中，DR2将退化图像转化为粗糙、平滑和视觉上清晰的中间结果，这些结果属于一个退化不变的分布（图1中的第4列）。在第二阶段中，退化不变的图像通过增强模块进一步处理，以获得高质量的细节。通过这种设计，增强模块与各种修复方法的设计兼容，以寻求最佳的修复质量，确保我们的DR2E既具有强大的鲁棒性又具有高质量。第一阶段为了从降至$y$中获得估计图像${\hat{x}}_0$，并在第二阶段对估计的图像增强，目标是最大化以下似然：
$$\begin{array}{rl}{p}_{\psi ,\varphi }& =\int p_{\psi }(x|{\hat{x}}_0)p_{\varphi }({\hat{x}}_0|y)d{\hat{x}}_0\\ & ={\mathbb{E}}_{{\hat{x}}_0\sim p_{\varphi }({\hat{x}}_0|y)}[p_{\psi }(x|{\hat{x}}_0)]\end{array}\text{\hspace{1em}(1)}$$
其中，$p_{\varphi }({\hat{x}}_0|y)$对应着复原模型，$p_{\psi }(x|{\hat{x}}_0)$对应着增强模块。对于第一阶段，我们提出了一个重要的假设，并提出了一种基于扩散的方法来消除退化，而不是直接学习从$y$到$x$的映射（通常涉及预定义的退化模型$z$）。

3.1 基于扩散的降质移除

假设：扩散过程中，存在一个中间步$\tau$，且$t>\tau$，那么存在$q(x_t|x)$和$q(y_t|y)$在低频部分是接近的，此外，存在$\omega >\tau$使得$q(x_{\omega }|x)\approx q(x_{\omega }|x)$，这个假设的意思的，你前向过程加入了噪声破坏了图像的频率成分，而噪声图同样也是，在视觉上对某些频率部分是难以分辨的，但是这个假设不够强，只有在噪声足够大的时候才可以。根据这个假设我们可以获得：
$$\begin{array}{rl}{p}_{\varphi }({\hat{x}}_0|y)& =\int p_{(}{\hat{x}}_0|x_{\tau })p(x_{\tau }|y_{\omega })p(x_{\omega }|y)d{x}_{\tau }d{y}_{\omega }\\ & \approx \int p_{(}{\hat{x}}_0|x_{\tau })p(x_{\tau }|x_{\omega })p(x_{\omega }|x)d{x}_{\tau }d{x}_{\omega }\end{array}$$

1. 在$\omega$处初始化条件：将降质图像$y$通过扩散模型的前向过程获得$x:=y_{\omega }$
2. 进行一次逆扩散过程获得$x_{t-1}$，其中（$\tau +1\le t\le \omega$），同时对降质图像$y$进行一次前向过程采样得到$y_{t-1}$。根据假设，我们替换$x_{t-1}$的低频部分为$y_{t-1}$。和ILVR一样。
3. 在第$\tau$步截断输出：当$t$逐渐变小时，噪声强度变得温和且$q(x_t|x)$和$q(y_t|y)$之间的举例会逐渐变大，因此去噪过程需要在$t$足够小的时候进行阶段。我们直接在第$\tau$步估计出$x_0$。

3.2 图像增强

对于DR2的输出，恢复高质量的细节只需要训练增强模块$p_{\psi }(x|{\hat{x}}_0)$。在这里，我们不假设这个模块的具体方法或架构。任何可以训练成将低质量图像映射到高质量图像的神经网络都可以插入我们的框架中。并且利用所提出的损失函数对增强模块进行独立训练。

4. 实验

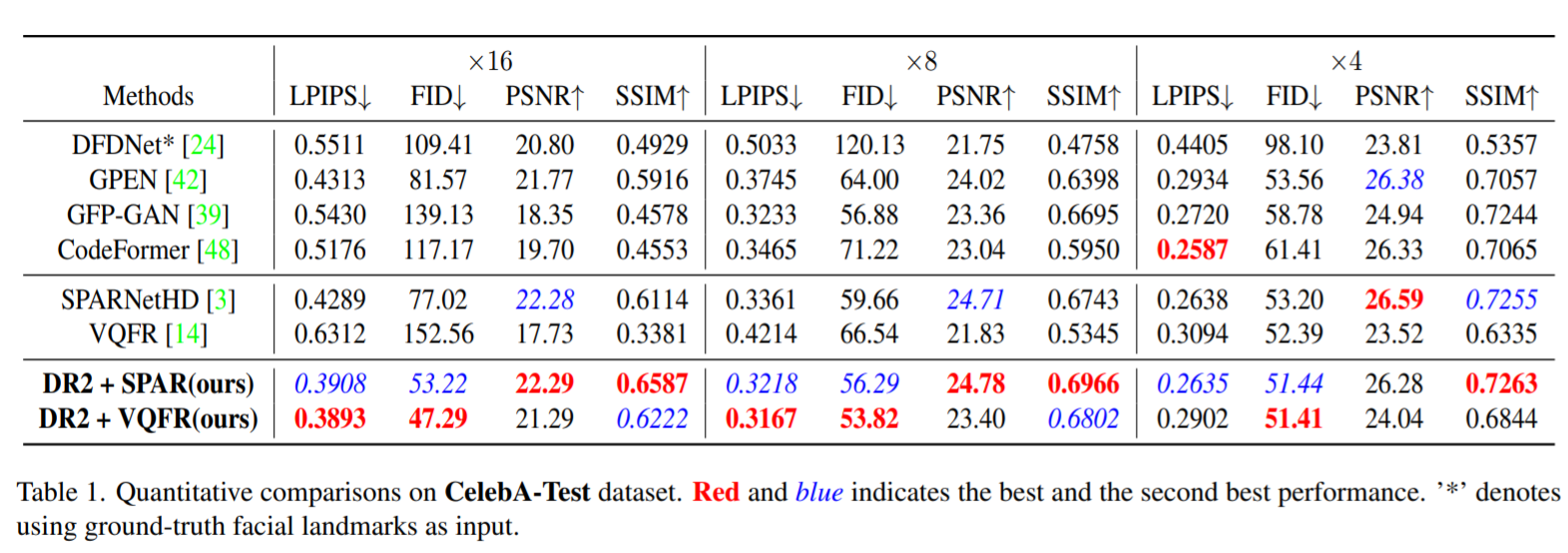
实施DR2和增强模块在FFHQ数据集上独立训练，该数据集包含70000张高质量人脸图像。我们将ILVR提出的预训练DDPM用于我们的DR2。我们选择SPARNetHD和VQFR作为增强模块的两种替代架构。

4.1 指标和可视化对比