无约束

之前梯度类算法中介绍的最速下降法、牛顿法和拟牛顿法，可以直接使用的条件之一为：决策变量都是无约束的。

用数学语言描述的话，可以表达为：决策变量为$x=(x_1,x_2,\cdot \cdot \cdot ,x_n)$，目标函数为
$$minf(x)$$

但在实际问题中，大部分都是包含约束的，比如多个决策变量之间存在耦合关系、资源有上限等。其中，有些是等式约束，有些则是不等式约束。在求解这类包含约束的最优化问题时，就需要一些新的方法。本文主要介绍拉格朗日乘子法和KKT条件。

等式约束

当最优化问题中只包含等式约束时，数学模型可以表达为
$$\begin{gathered} minf(x) \\ \text{s.t.}{h}_l(x)=0,l=1,2,...,L \end{gathered}$$
相比无约束的情况，多了$h_l(x)=0$的限制。

求解这类问题的思路是，想办法将等式约束去掉，将原问题转化为无约束优化问题，这样就可以使用梯度类算法求解了。

拉格朗日乘子法是很常用的一种转化方法，该方法是构造如下的优化问题：
$$minL(x,\lambda )$$
其中
$$L(x,\lambda )=f(x)+\sum _{l=1}^L{\lambda }_l{h}_l(x)$$
相比原优化问题，新优化问题是无约束的，但是多了一组优化变量$\lambda$。看起来，两者是有些差异的，那么它们的最优解是否相同呢？答案是相同的，接下来详细解释一下。

针对$L(x,\lambda )$，求一阶导数，并令其等于0：
$$\begin{gathered} \frac{\partial L}{\partial x_i}=0\Rightarrow \frac{\partial f}{\partial x_i}+\sum _{l=1}^L{\lambda }_l\frac{\partial h_l}{\partial x_i}=0 \\ \frac{\partial L}{\partial {\lambda }_l}=0\Rightarrow h_l=0 \end{gathered}$$
上述两式即为$L(x,\lambda )$取极值的必要条件。第一个公式暂时不需要关心，主要看第二个公式$h_l=0$。也就是说，假设存在一组$(x^{\ast },{\lambda }^{\ast })$使得$L(x,\lambda )$取到极值点，那么必然有
$$h_l(x^{\ast })=0$$
即等式约束已经被满足。此时
$$L(x^{\ast },{\lambda }^{\ast })=f(x^{\ast })$$
即最优解也等价。

虽然已经证明了，但好像依然挺绕的。接下来再画一个二维最优化问题的示意图，直观理解一下。

如下图所示。蓝色曲线为约束条件，所以可行解只能在该曲线上。3条黑色圈为原目标函数$f(x,y)$的等高线，其值从外向内越来越小，分别为5、3和1。蓝色曲线和黑色等高线存在3种空间关系，分别是不相交、相交和相切。针对不相交的情况（图中C点），显然$h(x,y)\ne 0$，所以是不可行解；针对相交的情况（图中B点），从相交点开始，沿着等高线降低方向寻找，必然存在更优解；针对相切的情况（图中A点），则恰好为最优解。

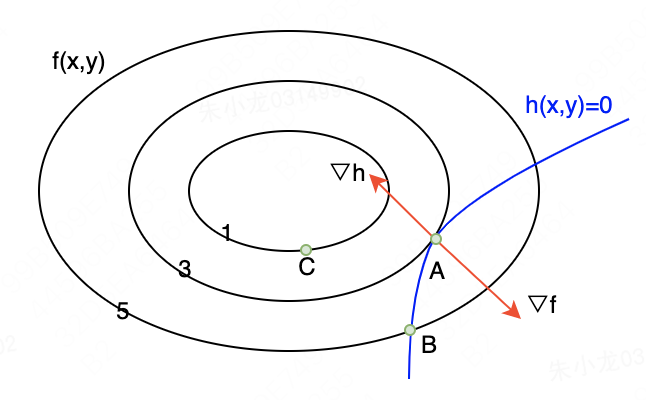
现在来看一下相切点处的特征。首先是$h(x,y)=0$，即$L(x,\lambda )$取极值的第二个必要条件，自必不多说；其次是由于相切，$f(x,y)$和$h(x,y)$的法向量共线，即梯度共线，由此可以推导出$L(x,\lambda )$取极值的第一个必要条件。所以，原问题和新问题是完全等价的。

这里还需要额外说的一点是：图中$\Delta f$的方向肯定是向外的，因为梯度的定义表明了其是指向$f$变大方向的；但是$\Delta h$的方向是不明确的，因为我们只有$h(x,y)=0$的信息，并不清楚朝哪个方向能让$h(x,y)$变大，所以图中只是一个示意图。

不等式约束

如果最优化问题中不仅包含等式约束，还包含不等式约束，数学模型可以表达为
$$\begin{gathered} minf(x) \\ \text{s.t.}{h}_l(x)=0,l=1,2,...,L \\ {g}_m(x)\le 0,m=1,2,...,M \end{gathered}$$

求解该类问题的思路也很简单：先将不等式约束$g(x)$转化为等式约束，然后再按照第二节中介绍的拉格朗日乘子法继续求解。

将不等式约束变为等式约束的方式是增加松弛变量$w_m^2$：
$$g_m(x)+w_m^2=0,m=1,2,...,M$$
至此，可以构造新的拉格朗日函数：
$$L(x,\lambda ,w)=f(x)+\sum _{l=1}^L{\lambda }_l{h}_l(x)+\sum _{m=1}^M{\lambda }_{L+m}[g_m(x)+w_m^2]$$

求一阶导数，可以得到最优解的必要条件如下：
$$\begin{gathered} \frac{\partial L}{\partial x_i}=0\Rightarrow \frac{\partial f}{\partial x_i}+\sum _{l=1}^L{\lambda }_l\frac{\partial h_l}{\partial x_i}+\sum _{m=1}^L{\lambda }_{L+m}\frac{\partial g_m}{\partial x_i}=0 \\ \frac{\partial L}{\partial {\lambda }_l}=0\Rightarrow h_l=0,g_m+w_m^2=0 \\ \frac{\partial L}{\partial w_m}=0\Rightarrow 2{\lambda }_{L+m}{w}_m=0 \end{gathered}$$

KKT条件

事实上，针对包含不等式约束的情况，除了先转化为等式约束再使用拉格朗日乘子法这种“曲线救国”的方法，还有更直接的求解方法，那就是KKT条件。

针对上述同时包含等式和不等式约束的最优化问题，KKT条件为
$$\begin{gathered} \frac{\partial f}{\partial x_i}+\sum _{l=1}^L{\lambda }_l\frac{\partial h_l}{\partial x_i}+\sum _{m=1}^L{\lambda }_{L+m}\frac{\partial g_m}{\partial x_i}=0 \\ {h}_l=0,g_m\le 0 \\ {\lambda }_{L+m}{g}_m=0 \\ {\lambda }_{L+m}\ge 0 \end{gathered}$$

需要注意的有三点：
（1）相比上一节转化的拉格朗日乘子法，KKT中新增了约束${\lambda }_{L+m}\ge 0$；
（2）相比KKT条件，拉格朗日乘子法中新增了变量$w$；
（3）拉格朗日乘子法中的${\lambda }_{L+m}{w}_m=0$和KKT条件中的${\lambda }_{L+m}{g}_m=0$是等价的。

接下来理解一下KKT条件。

假设$x^{\ast }$为原问题的最优解。针对$g(x^{\ast })$，存在两种可能性：
（1）$g(x^{\ast })<0$。此时该约束没起到作用，可以直接去掉，问题退化为第二节的等式约束问题，此时${\lambda }_{L+m}=0$即可。
（2）$g(x^{\ast })=0$。此时该约束相当于新的等式约束，把第二节中的二维最优化图再搬运过来看一下。到了这里后，我们发现，$f(x,y)$和$g(x,y)$的法向量不仅要共线，而且方向还一定要恰好相反，即$g(x,y)<0$必然在右侧。这是因为如果$g(x,y)<0$在左侧，则C点满足不等式约束，且目标函数值比A点更优，与$g(x^{\ast })=0$矛盾。

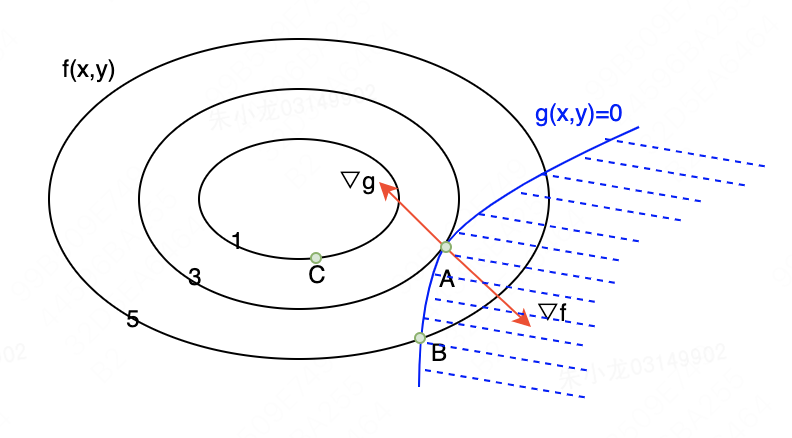
综上可以推导出：${\lambda }_{L+m}{g}_m=0$和${\lambda }_{L+m}\ge 0$。