Cramer-Shoup密码系统来自于A Practical Public Key CryptosystemProvably Secure against Adaptive ChosenCiphertext Attack这篇论文
CDH问题回顾：
已知(g,g^x, g^{k)能否计算g}xk
DDH问题回顾：
已知(g,g^x, g^k ，D)能否判断D是否等于g^xk
注意：在双线性映射下DDH问题不是困难问题
原因：e^( g^x, g^k) 是否等于e^(g,D)可以判断出来
BDH问题：
在双线性映射下两个不是困难问题，三个就是了
e^(g, g^x, g^y , g^z,D)判断D是否等于 g^xyz
ElGamal加密体制回顾：
对于任意的x，
y=g^x
sk=x.
pk=y,
C1=g^k,
c2=m*y^k
m=C2/C1^x

ElGamal在CPA下安全<=====>CDH问题是困难问题
证：
=>
（反证法）假设CDH问题可解，则ElGamal在CPA下不安全
C1=g^k,
c2=m*y^k，）
(g,g^x ,g^k ,g^xk)中 g^xk可以计算出来
因为m=C2/g^xk
<
假设ElGamal在CPA下不安全，则CDH问题可解
若已知(g,g^x ,g^k)可以解出m
那么(g,g^x ,g^k ,g^xk,C2/m)
C2/m=g^xk
Simulator用来解数学难题，将A作为子程序来攻破方案
Hash函数：提供认证功能
hash函数具有单向性（H(s)=m，求不出s）和抗碰撞性（x1≠x2，求不出H(x1)=H(x2)）
CPA（选择明文攻击）：

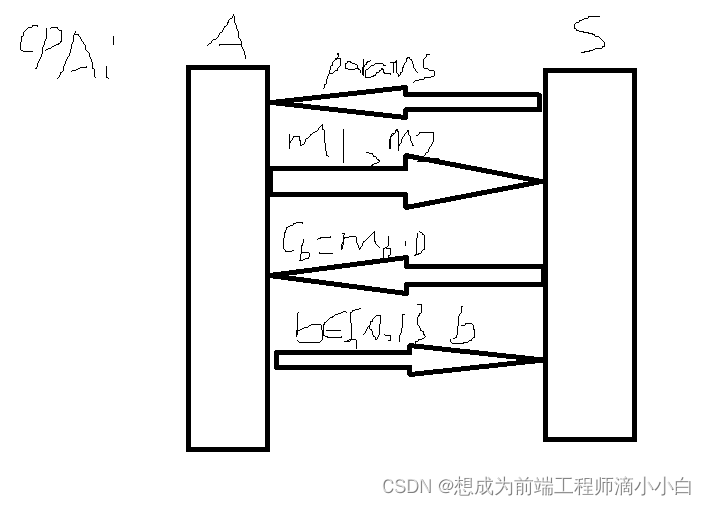
CCA2（自适应选择密文攻击）：

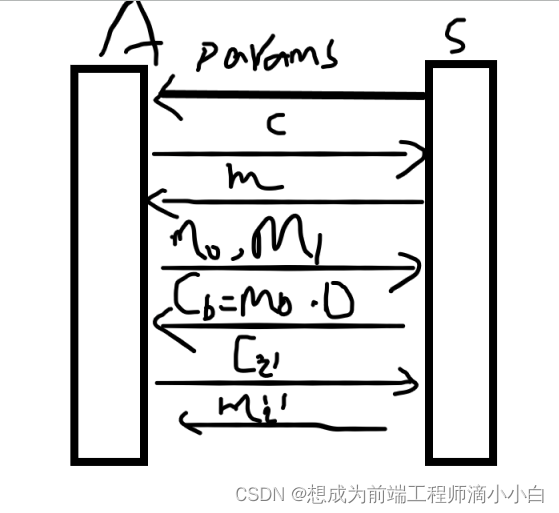
ElGamal加密体制不能抵制CCA2：D相当于将明文mb隐藏了，其中D没起作用