一、判断一个链表是否有环

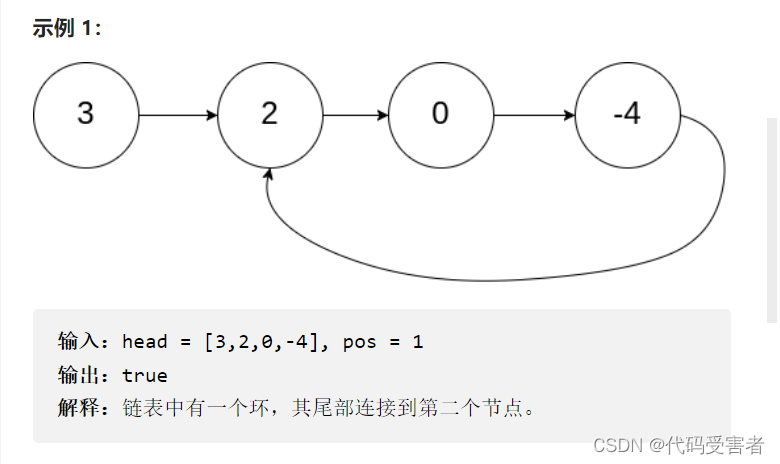
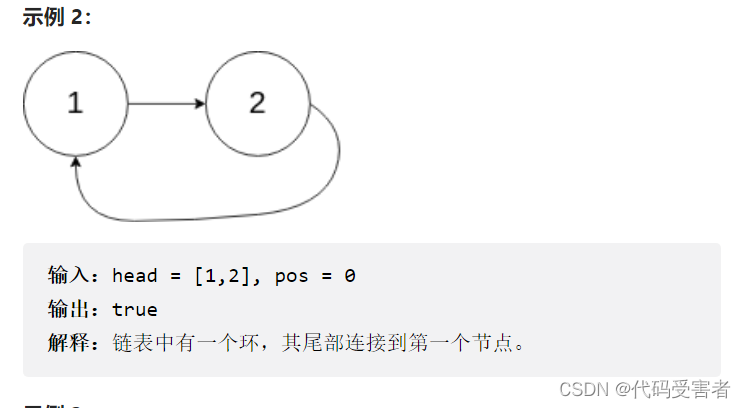
给你一个链表的头节点 head ，判断链表中是否有环。
如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ，则返回 true 。 否则，返回 false 。



解题思路:

用快慢指针，慢指针一次往后走一步，快指针一次往后走两步。这样快指针会比慢指针先入环，当慢指针入环被快指针追上时，说明这是一个环形链表，当快指针为空或者指向空时，说明这不是环形链表，返回NULL。

为什么肯定slow 和 fast一定会相遇呢？我们假设当slow入环时，fast到slow的距离为N。

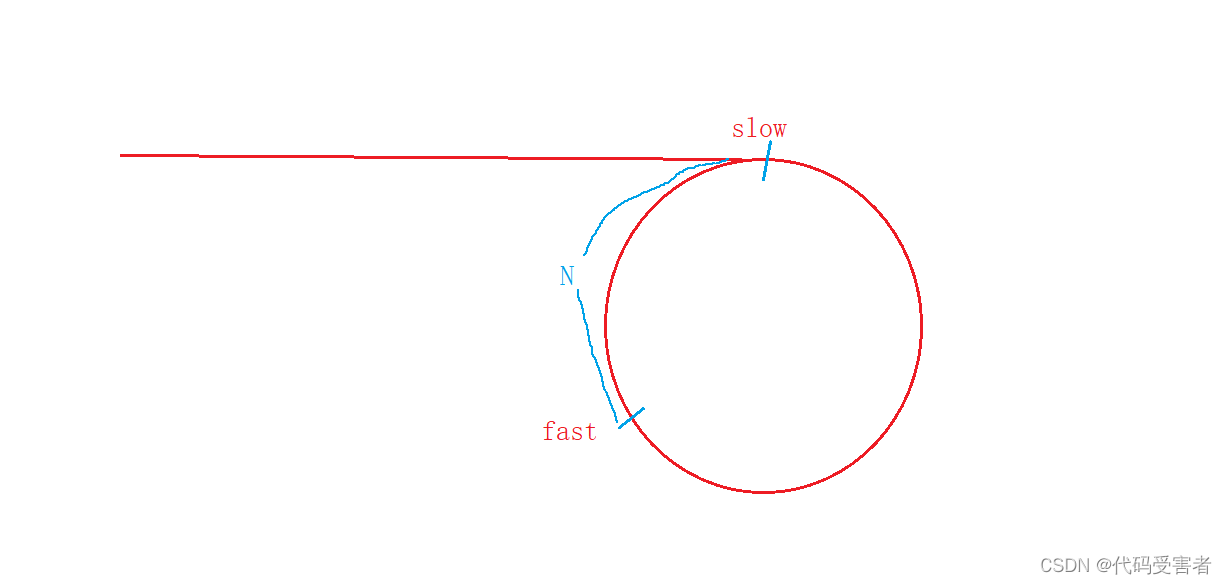
而slow 每次往前走一步，fast 每次往前走两步，那么它们的距离是逐渐递减的。

最后它们之间的距离为 0 时，它们就相遇了。

那问题来了，如果fast 一次走三步，四步，五步，它能不能在环中与slow相遇呢？ 我们假设fast一次走三步。
fast到slow的距离继续为N

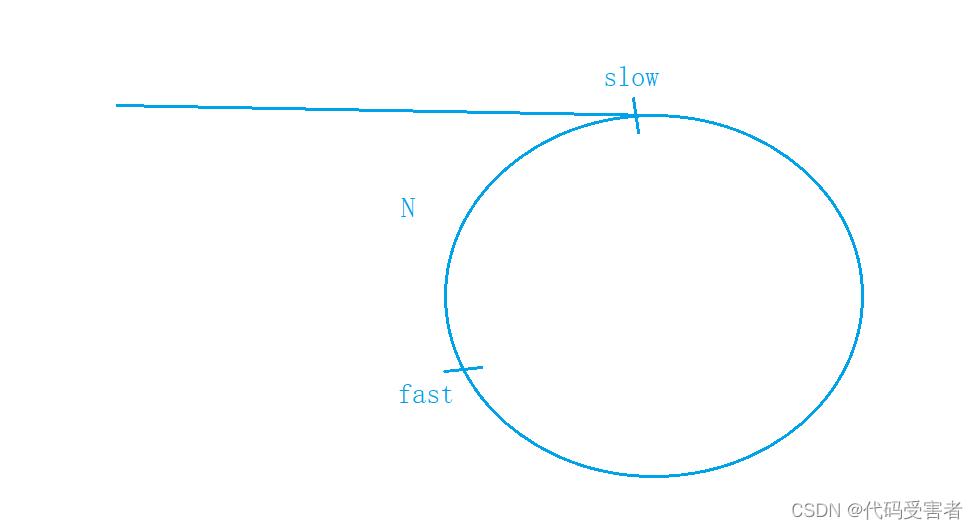
slow 一次走一步， fast一次走三步 ， 那么N是每次少2

此时会出现两者情况，一种情况是相遇了，还有一种情况是没相遇。
当没相遇的时候，fast已经跑到了 slow的前面，也就是它们此时的距离是-1。

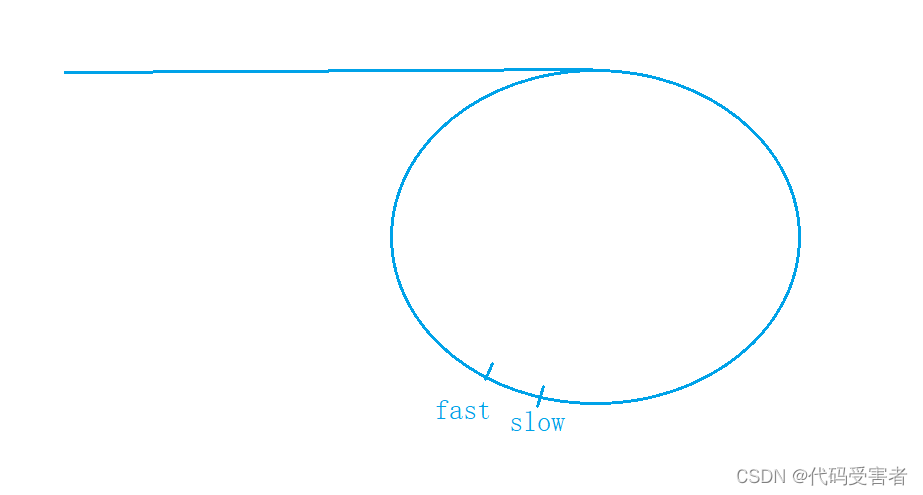
设这个环的长度为C，所以它们的距离 N 此时是等于 C-1的。而因为fast一次是走三步的，所以N每次会-2。 当N等于0时它们才会相遇，这也就意味，C-1 如果是偶数，那么它们才会相遇，如果C-1 是奇数，那它们永远不会相遇。所以，fast 一次走两步，它一定会和slow在环里面相遇，slow不用走完一圈。如果fast一次走3，4，5…n步，那么是有可能永远不会与slow相遇的。

代码如下:

bool hasCycle(struct ListNode *head) {
    struct ListNode* slow = head;
    struct ListNode* fast = head;

    //如果fast为空或者指向空，说明不是环形链表
    while(fast && fast->next)
    {
        //慢指针一次走一步，快指针走两步
        fast = fast->next->next;
        slow = slow->next;

        //如果fast 与 slow 相遇，说明是环形链表
        if(fast == slow)
        {
            return true;
        }
    }
    //出了循环，说明不是环形链表
    return false;
}

题目链接

二、找到链表入环的第一个节点

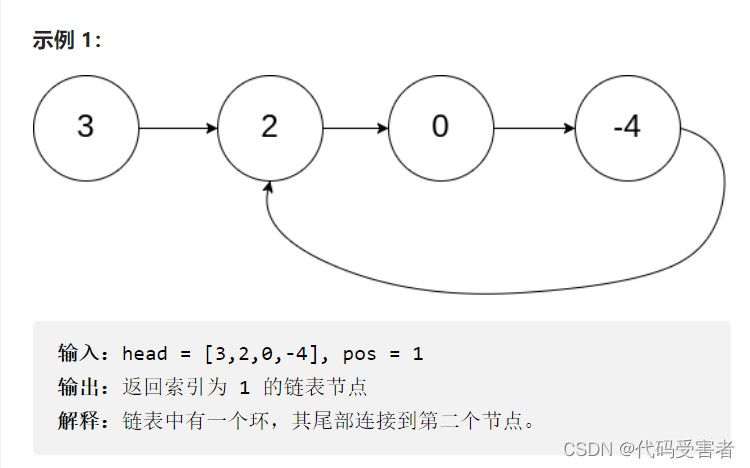
判断了一个链表是否有环之后，那么如何找到链表入环的第一个节点呢？我们设链表头节点到入环的第一个节点为L。

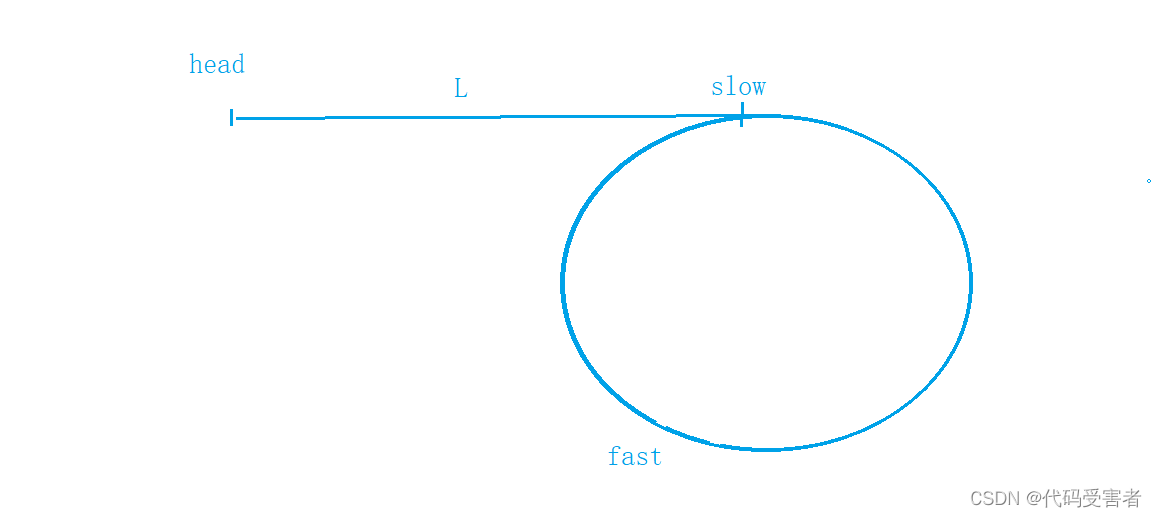
我们再设 入环的第一个节点，到slow 与fast相遇的节点的距离为X。

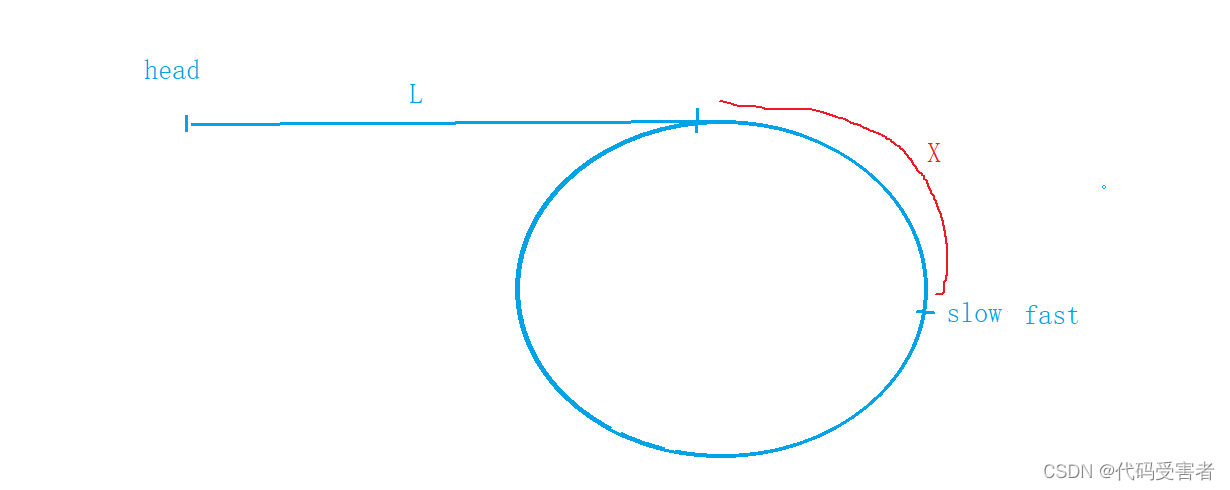
那么slow 走的距离是 L + X
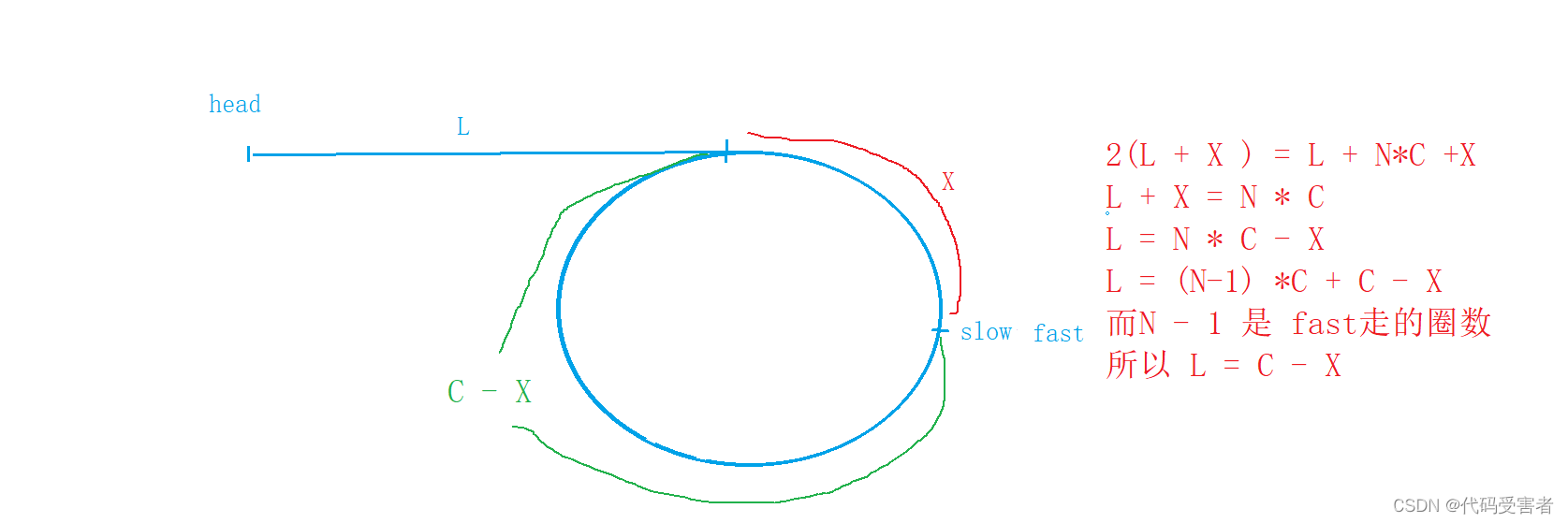
设圆的长度为C
那么fast走的距离是 L + NC + X
N代表走的圈数，因为当环长度很小，而L长度非常大的时候，slow 入环时，fast 不可能只走一圈，一圈是极端情况，这样我们就可以推导出。
2(L + X ) = L + NC +X
L + X = N * C
L = N * C - X
L = (N-1) *C + C - X
而N - 1 是 fast走的圈数，我们可以省掉
所以 L = C - X

代码:

struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode* slow , *fast;
    slow = fast = head;
    while(fast && fast->next)
    {
       
        fast = fast->next->next;
        slow = slow->next;

         if(fast == slow)
        {
            //保存相遇节点
            struct ListNode* MeetNode = slow;
            struct ListNode* NewHead = head;
            //相遇点和头节点同时走
            while(MeetNode != NewHead)
            {
                MeetNode =  MeetNode->next;
                NewHead =   NewHead->next;
            }
            return MeetNode;
        }
    }
    return NULL;
}

当然，这题还有第二种方法，不过容易理解，实现起来可能有点困难。
我们可以把相遇节点的下一个节点，作为一个新链表的头节点，而上一个节点作为两个链表的尾节点。而这俩个相交的节点，就是入环的第一个节点

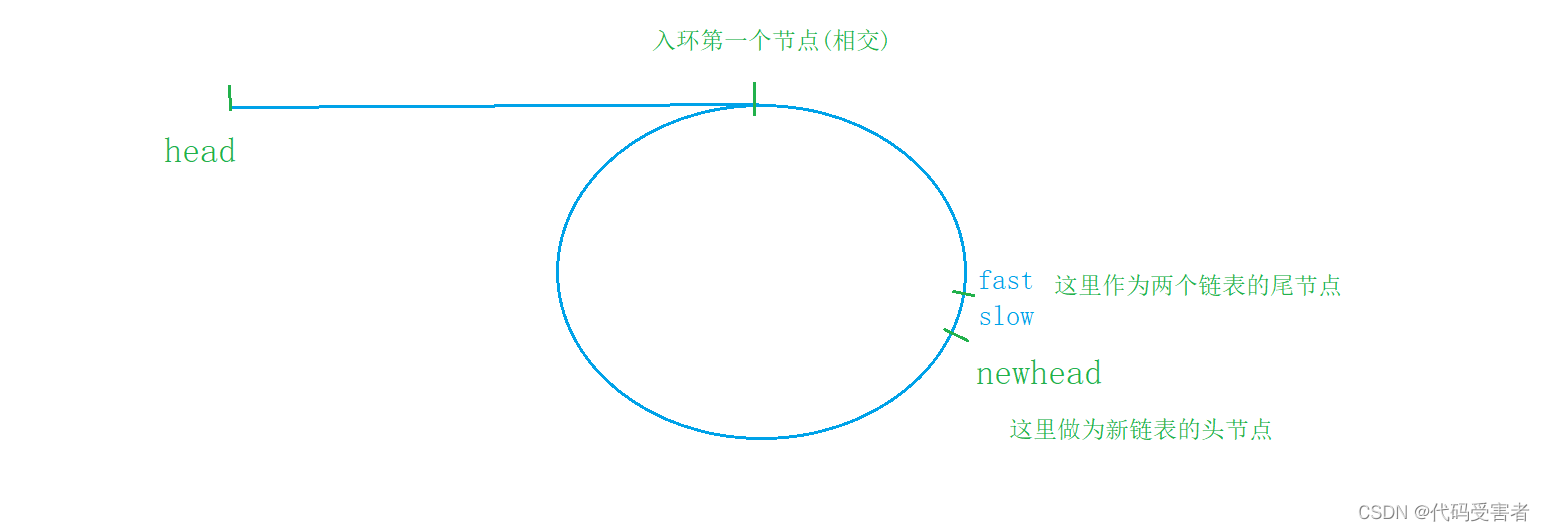
至于如何找到两个链表的交点，上一篇博客第八题有说明，传送地址

所以第二种方法，我们只需要找到它们的newhead和head的相交节点就可。

代码

struct ListNode *detectCycle(struct ListNode *head) {
        struct ListNode* slow , *fast;
        slow = fast = head;

        while(fast && fast->next)
        {
            slow = slow->next;
            fast = fast->next->next;

            //如果俩节点相遇
            if(slow == fast)
            {
                //新节点为相遇的下一个节点
                struct ListNode* NewHead = slow->next;
                struct ListNode* OldHead = head;
                //求出新节点 和 原头节点 到 尾节点(slow)的长度 
                int lenNew = 1;
                int lenOld = 1;
                while(NewHead != slow)
                {
                    NewHead = NewHead->next;
                    lenNew++;
                }

                while(OldHead!= slow)
                {
                    OldHead = OldHead->next;
                    lenOld++;
                }
                //相差多少个长度
                int gap = abs(lenOld - lenNew);
                //找到较长和较短的链表
                struct ListNode* LongList = head;
                struct ListNode* ShortList = slow->next;
                if(lenOld < lenNew)
                {
                    LongList = slow->next;
                    ShortList = head;
                }
                //让长节点先走gap次
                while(gap--)
                {
                    LongList = LongList->next;
                }
                //然后俩个节点同时走
                while(LongList != ShortList)
                {
                    LongList = LongList->next;
                    ShortList = ShortList->next;
                }
                //此时就是相交节点
                return ShortList;
            }

        }
    return NULL;
}

题目链接