引言

        本系列博客旨在为机器学习(深度学习)提供数学理论基础。因此内容更为精简，适合二次学习的读者快速学习或查阅。

---

1、参数范数惩罚

        通过对目标函数 $J$ 添加一个参数范数惩罚 $\Omega (\theta )$ ，限制模型的学习能力。将正则化后的目标函数记为 $$\tilde{J}(\theta ;X,y)=J(\theta ;X,y)+\alpha \Omega (\theta )$$
        其中 $\alpha \in [0,\infty )$ 是权衡范数惩罚项 $\Omega$ 和标准目标函数 $J(X;\theta )$ 相对贡献的超参数。 $\alpha$ 越大，对应的正则化惩罚越大。

2、 $L^2$ 正则化

        定义： $$\Omega (\theta )=\frac{1}{2}||w|{|}_2^2$$
        性质：
        （1）$L^2$ 正则化可以使权重更加接近原点，降低模型复杂度，从而防止过拟合。
        （2）$L^2$ 正则化能让学习算法“感知”到具有较高方差的输入 $x$ ，因此与输出目标的协方差较小（相对增加方差）的特征的权重将会收缩。

3、 $L^1$ 正则化

        定义：$$\Omega (\theta )=||w|{|}_1=\sum _i|w_i|$$
        性质：
        （1）相比 $L^2$ 正则化， $L^1$ 正则化会产生更稀疏的解，即，最优值中的一些参数为0。
        （2）由于 $L^1$ 正则化具有稀疏性质，所以广泛应用于特征选择。

4、显式约束和重投影

        通过上述正则化策略，我们可以将网络权重 $\theta$ 限制到某个区域内，如， $L^2$ 正则化中会将网络权重限制到一个 $L^2$ 球中。虽然我们可以通过控制参数 $\alpha$ 来调整限制区域的大小，但通常我们难以知道这个限制区域的确切大小。因此需要进行显式约束：我们希望约束 $\Omega (\theta )$ 小于某个常数 $k$ 。
        为了实现显式约束，我们需要修改反向传播中的梯度下降算法，实现重投影：
        （1）正常按照无任何约束情况，计算得到 $J(\theta )$ 的梯度。
        （2）对参数 $\theta$ 进行更新。
        （3）将更新后的参数 $\theta$ 投影到满足 $\Omega (\theta )<k$ 的最近点。
        相比使用惩罚强加约束，使用显式约束和重投影的优点如下：
        （1）惩罚可能会导致目标函数非凸而使算法陷入局部极小。而重投影实现的显式约束则没有直接改变优化目标，只是限制权重变得异常大甚至离开限制区域。
        （2）重投影实现的显式约束对优化过程增加了一定的稳定性：当使用较高的学习率时，很可能进入正反馈，即大的权重诱导大梯度，然后使得权重获得较大更新，从而让网络更快地探索参数空间，而且同时还不会让权重脱离限制区域。

5、参数绑定和参数共享

        另一种对网络权重 $\theta$ 进行限制的思路是参数绑定和参数共享，这样做的显著优点是，只有参数的子集需要被存储在内存中，可以显著减少模型的内存占用。
        目前为止，最流行和广泛使用的参数共享出现在应用于计算机视觉的卷积神经网络(CNN)。参数共享显著降低了CNN模型的参数数量，从而显著提高了网络的规模(深度)。
        循环神经网络也是参数共享的最佳实践。

6、Bagging

        Bagging 是通过结合几个模型降低泛化误差的技术。主要想法是分别训练几个不同的模型，然后让所有模型表决测试样例的输出。这是机器学习中常规策略的一个例子，被称为模型平均。采用这种策略的技术被称为集成方法。
        模型平均奏效的原因是不同的模型通常不会在测试集上产生完全相同的误差。

7、Dropout

        在深度学习中，Bagging 似乎不太实用了。因为训练一个模型就已经很不容易了(大一点的可能要训练几天)，想要训练一群模型进行 Bagging，这是不现实的。而 Dropout 提供了一种 Bagging 的廉价的近似方法。
        Dropout 训练的集成包括所有从基础网络除去非输出单元后形成的子网络。即在训练中，对于每一个训练样本随机令神经单元按照一定概率 $p$ 被包括，如下图所示：
        
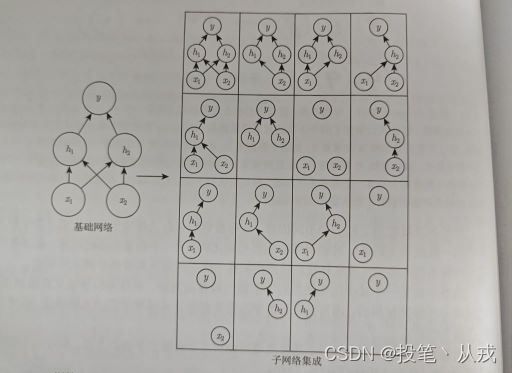
        Dropout 训练与 Bagging 不太一样。Bagging 中的所有模型都是独立的，但在 Dropout 的情况下，所有模型共享参数，其中每个模型继承父神经网络参数的不同子集。参数共享使得在有限可用内存下表示指数级数量的模型变得可能。
        对于上图中的基础网络，使用 Dropout 后的计算图如下所示，其中 $\mu$ 是二项式分布，训练过程中每一次前向传播和反向传播都会随机生成一次，表示有概率 $p$ 被包括：

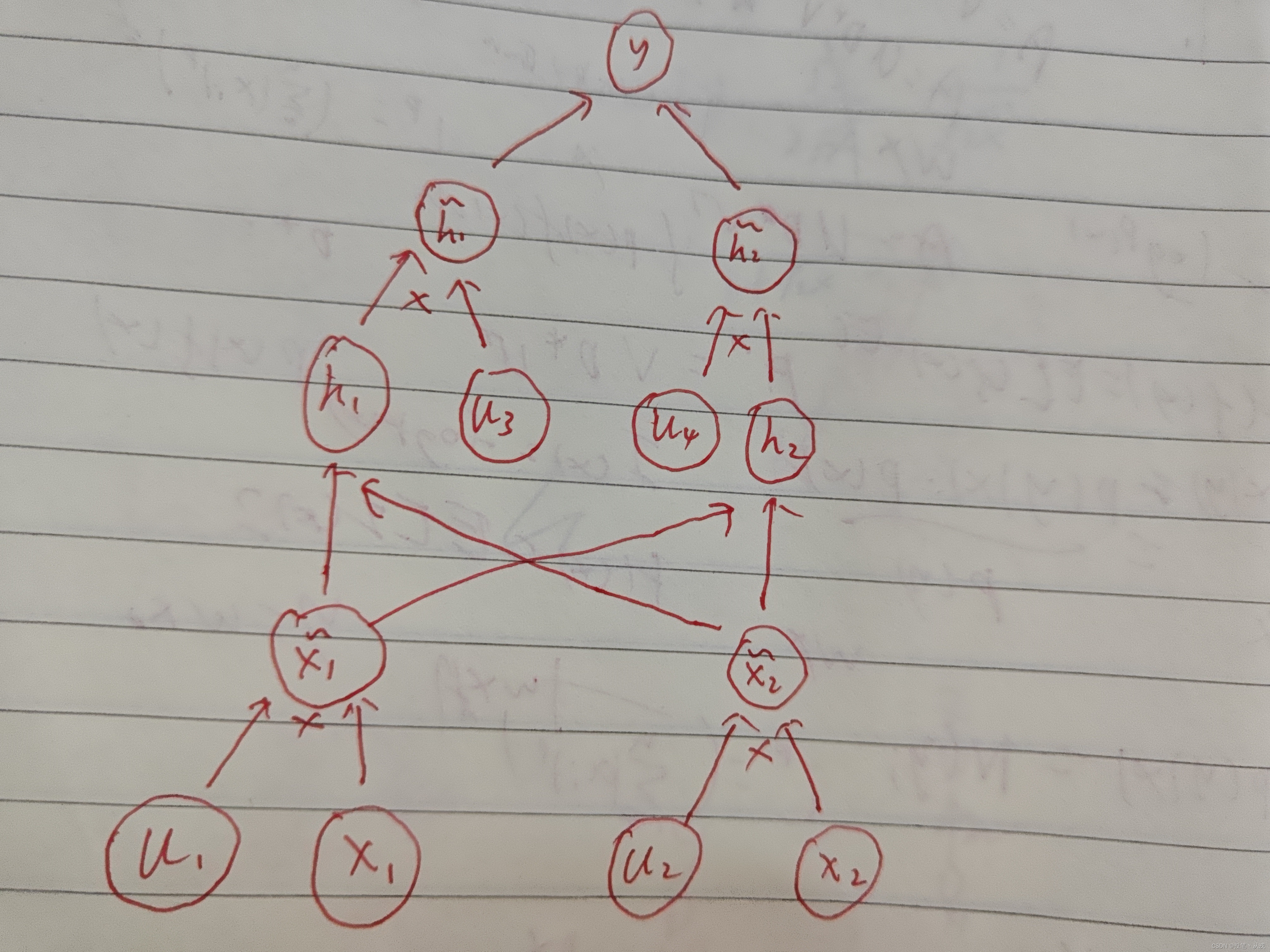
        权重比例推断规则：到了测试阶段，就不能再使用 Dropout 了，因为这会导致模型不稳定，即每一次相同的输入会产生不同的输出。因此，为了在测试阶段得到稳定且正确的结果，需要使用权重比例推断规则。该规则有两种实现方式：
        （1）训练结束后将单元权重 $\theta$ 乘以被包括的概率 $p$ 。
        （2）训练期间将单元的输出 ${\tilde{x}}_1$ 除以被包括的概率 $p$ 。
        无论是哪种实现方式，其目的都是为了确保在测试阶段单元的期望输出与在训练阶段该单元的期望输出是大致相同的。
        Dropout 的性质如下：
        （1）适用于训练数据集较多的场景。
        （2）Dropout 不仅仅是训练一个 Bagging 的集成模型，而且是共享隐藏单元的集成模型。
        （3）Dropout 强大的大部分原因来自施加到隐藏单元的掩码噪声。即可以看作对输入内容的信息高度智能化、自适应破坏的一种形式，而不是对输入原始值的破坏。破坏提取的特征而不是原始值，让破坏过程充分利用模型迄今获得的关于输入分布的所有知识。