Ⅰ. 归并排序
1. 基本思想
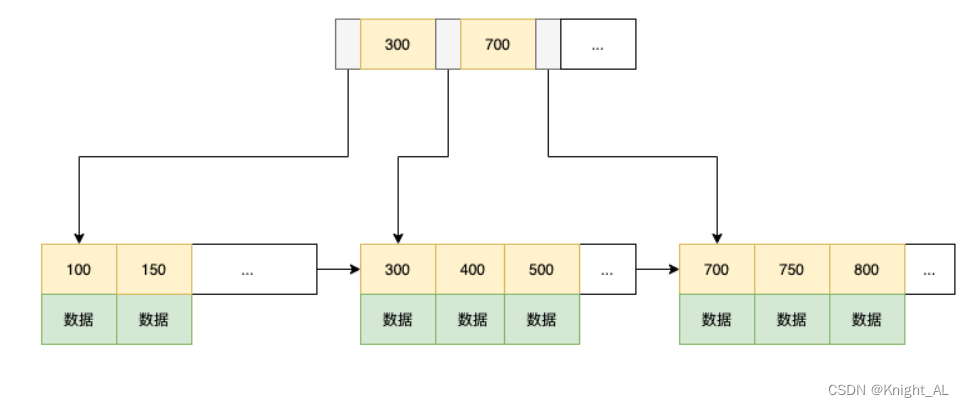
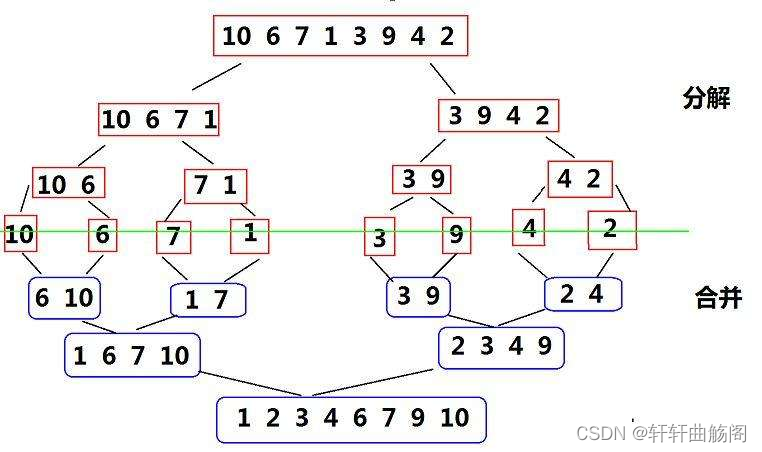
归并排序( MERGE-SORT )是建立在归并操作上的一种有效的排序算法 , 该算法是采用分治法( Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
图示如下
2. 递归代码实现
//打印数组内容
void ArrPrint(int* a, int n)
{
int i = 0;
for (i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
void _MergeSort(int* a, int begin, int end, int* tmp)
{
//当右边的下标小于左边时,结束递归
if (begin >= end)
{
return;
}
//取中间数mid,将当前内容二分为[begin, mid],[mid+1, end]
int mid = (begin + end) / 2;
//如果需要排序后半的话就必须重置一个新的begin来保证是从后半的位置开始(而非0处)
int begin1 = begin;
//如果需要排序前半的话就必须重置一个新的end来保证是在前半的位置结束(而非n-1处)
int end1 = mid;
//保证形式的统一
int begin2 = mid + 1;
int end2 = end;
_MergeSort(a, begin1, end1, tmp);
_MergeSort(a, begin2, end2, tmp);
//在从最后的递归返回后,返回的是前后两个有序的数组
//起点与终点分别是arr1:[begin1, end1] arr2:[begin2, end2]
//单趟归并
int begin3 = begin1;//记录前数组begin1的位置,作为tmp的起始位置
//当遍历完两个数组中的其中一个时,结束循环
while (begin1 <= end1 && begin2 <= end2)
{
//两数组中较小的数取出并存放在tmp对应位置上
if (a[begin1] < a[begin2])
{
tmp[begin3++] = a[begin1++];
}
else
{
tmp[begin3++] = a[begin2++];
}
}
//将剩下那个数组的值接在tmp上
//两个数组都进行判断,因为有一个数组已经完成排序不会进入循环
while (begin1 <= end1)
{
tmp[begin3++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[begin3++] = a[begin2++];
}
//将tmp数组值拷贝回a
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n)
{
//创建一个大小与a相同的数组,归并返回数据
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
//传入数组左右下标进行排序
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
tmp = NULL;
}我们用以下代码来验证
void test()
{
int a[] = { 5,6,7,4,1,9,2,8,3,0 };
int sz = sizeof(a) / sizeof(a[0]);
MergeSort(a, sz);
ArrPrint(a, sz);
}
int main()
{
test();
return 0;
}有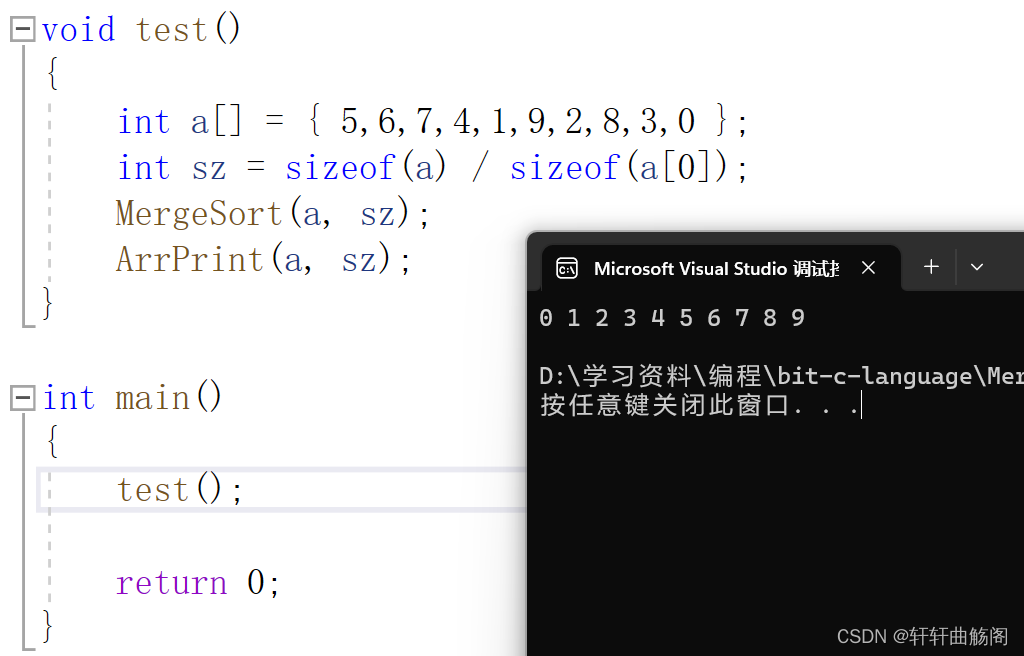
3. 非递归形式
对于有2的n次方个数据,如下的一组数据归并有
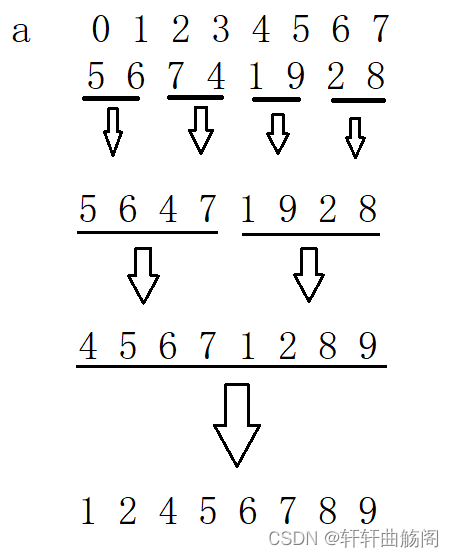
观察可以发现,第一次归并的间距为2(即2-0),第二次的间距为4(即4-0),由此我们可以得到如下代码
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
// 间隙为1,也代表2个一组进行归并
int gap = 1;
// 间隙为n/2时,代表n个一组归并
while (gap < n)
{
// 保证每次刚好归并排序对应2组的数据
for (int i = 0; i < n; i += gap * 2)
{
// 确定前后两组的头与尾
int begin1 = i, end1 = begin1 + gap - 1;
int begin2 = begin1 + gap, end2 = begin2 + gap - 1;
// 初始化tmp中开始储存数据的位置为begin1
int begin3 = begin1;
// 归并数据
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[begin3++] = a[begin1++];
}
else
{
tmp[begin3++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[begin3++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[begin3++] = a[begin2++];
}
// 从a+i的位置将有效数据从tmp全部拷贝回a
memcpy(a + i, tmp + i, sizeof(int)*(begin3 - i));
}
gap *= 2;
}
}而在大多数时候,数据个数并不总是2的n次方个数,因此需要我们作出修改,一般来说有如下几种情况
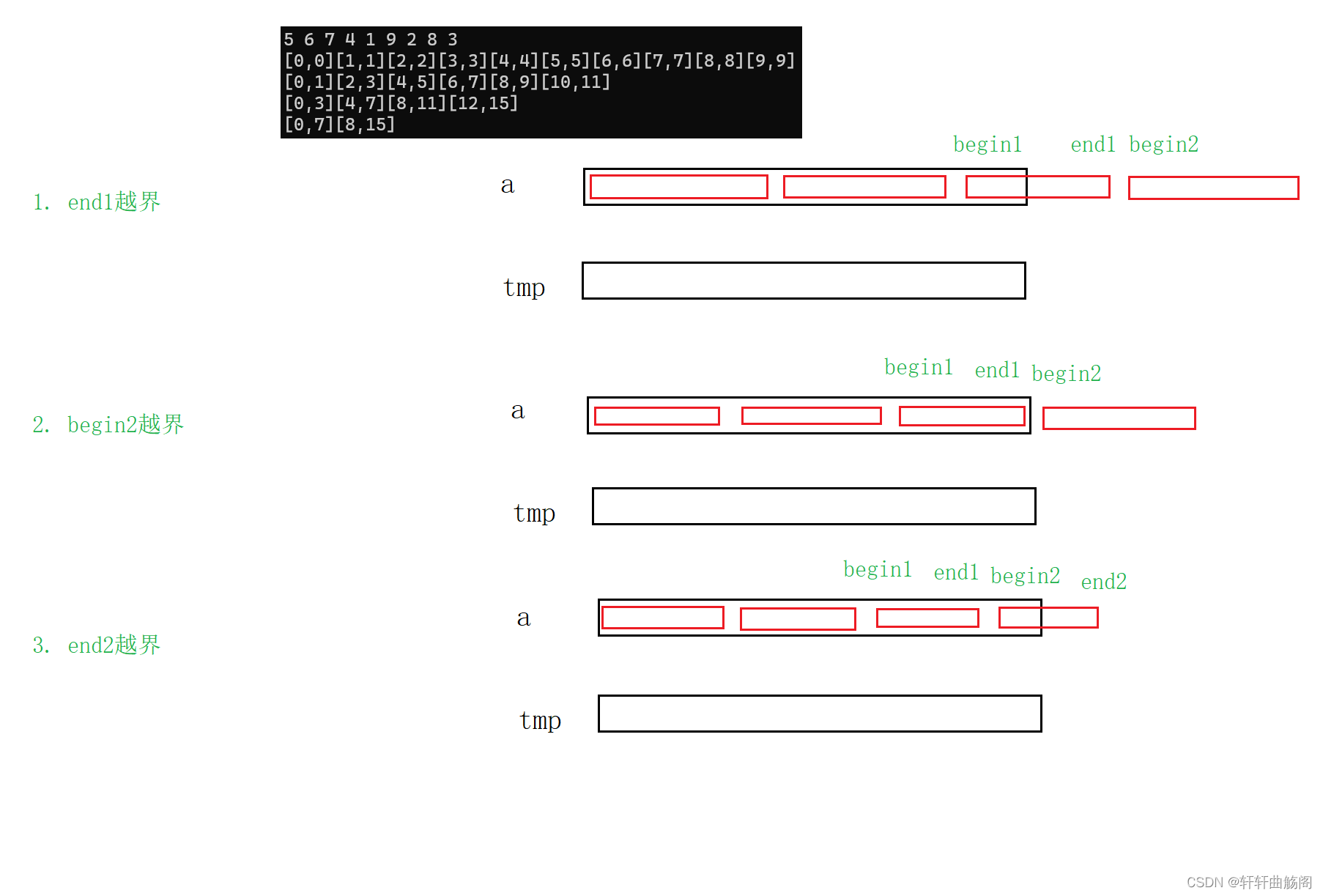
因此,有两种方案
一、将每次边界在数组外的部分存放在tmp中,最后一次性拷贝回a中
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
// 间隙为1,也代表2个一组进行归并
int gap = 1;
// 间隙为n/2时,代表n个一组归并
while (gap < n)
{
// 保证每次刚好归并排序对应2组的数据
for (int i = 0; i < n; i += gap * 2)
{
// 确定前后两组的头与尾
int begin1 = i, end1 = begin1 + gap - 1;
int begin2 = begin1 + gap, end2 = begin2 + gap - 1;
// 初始化tmp中开始储存数据的位置为begin1
int begin3 = begin1;
//第1种情况
if (end1 >= n)
{
// 将[begin1,end1]这一部分调整为end1截止,后面部分为不存在的区间
end1 = n - 1;
begin2 = n;
end2 = n - 1;
}
else if(begin2 >= n)// 第2种
{
// 将[begin1,end1]这一部分调整为end1截止,后面部分为不存在的区间
begin2 = n;
end2 = n - 1;
}
else if (end2 >= n)// 第3种
{
// 将[begin2,end2]这一部分调整为end2截止
end2 = n - 1;
}
// 手动打印边界查看范围
printf("[%d,%d][%d,%d]", begin1, end1, begin2, end2);
// 归并数据
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[begin3++] = a[begin1++];
}
else
{
tmp[begin3++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[begin3++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[begin3++] = a[begin2++];
}
}
// 将tmp的所有数据拷贝回a
memcpy(a, tmp, sizeof(int) * n);
printf("\n");
gap *= 2;
}
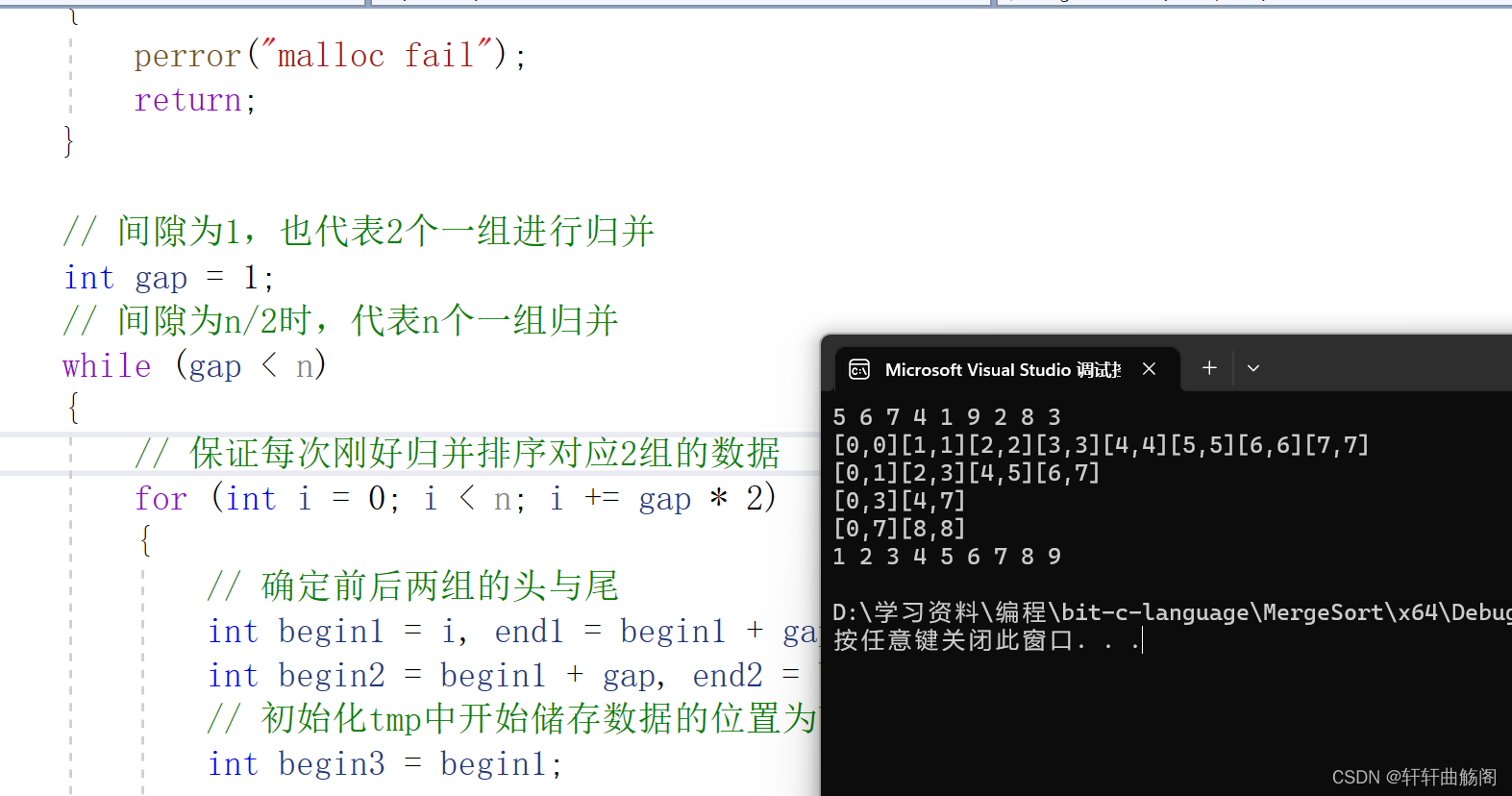
}验证有

二、将每次边界在数组外的部分放弃存放在tmp中,每次拷贝tmp的一部分回a中
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
// 间隙为1,也代表2个一组进行归并
int gap = 1;
// 间隙为n/2时,代表n个一组归并
while (gap < n)
{
// 保证每次刚好归并排序对应2组的数据
for (int i = 0; i < n; i += gap * 2)
{
// 确定前后两组的头与尾
int begin1 = i, end1 = begin1 + gap - 1;
int begin2 = begin1 + gap, end2 = begin2 + gap - 1;
// 初始化tmp中开始储存数据的位置为begin1
int begin3 = begin1;
// 第1,2种情况
if (end1 >= n || begin2 >= n)
{
// 只要end1或begin2越界,就放弃本次[begin1,end1]的排序
break;
}
else if(end2 >= n)// 第三种
{
// begin2未越界end2越界,将end2调整为最后一个元素进行排序
end2 = n - 1;
}
// 手动打印边界查看范围
printf("[%d,%d][%d,%d]", begin1, end1, begin2, end2);
// 归并数据
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[begin3++] = a[begin1++];
}
else
{
tmp[begin3++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[begin3++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[begin3++] = a[begin2++];
}
// 将tmp中对应数据数据拷贝回a
memcpy(a + i, tmp + i, sizeof(int) * (begin3 - i));
}
printf("\n");
gap *= 2;
}
}验证有
Ⅱ. 计数排序
1. 基本思想
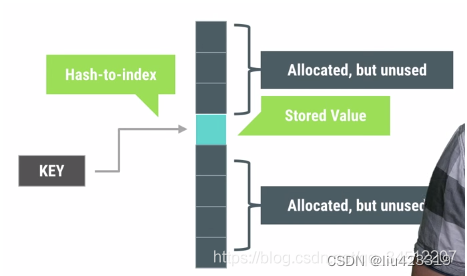
计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 操作步骤:1. 统计相同元素出现次数2. 根据统计的结果将序列回收到原来的序列中
即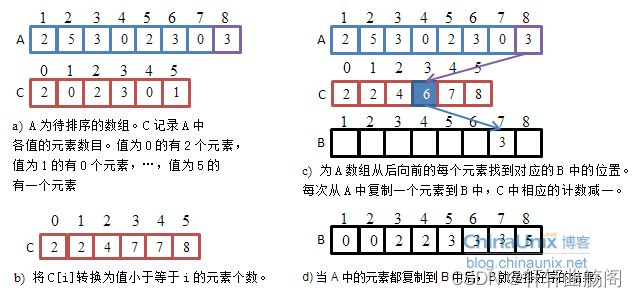
2. 代码实现
//打印数组内容
void ArrPrint(int* a, int n)
{
int i = 0;
for (i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
void CountSort(int* a, int n)
{
// 选出相对区间内的最大值与最小值
int min, max;
max = min = a[0];
for (int i = 0; i < n; i++)
{
if (max < a[i])
{
max = a[i];
}
if (min > a[i])
{
min = a[i];
}
}
// 创建一个大小数值在[min,max]内的临时数组
int* count = (int*)calloc((max - min + 1), sizeof(int));
if (count == NULL)
{
perror("calloc fail");
return;
}
for (int i = 0; i < n; i++)
{
// a[i] ∈ [min,max]
// a[i]-min ∈ [0,max-min]
// 因此对应下标++就代表对应数值+1
count[a[i] - min]++;
}
int j = 0;
// 将数值不为0的依次取出复制到原数组中
for (int i = 0; i < max - min + 1; i++)
{
// 对应计数数组为0时表明不含该元素
while (count[i]-- != 0)
{
a[j++] = i + min;
}
}
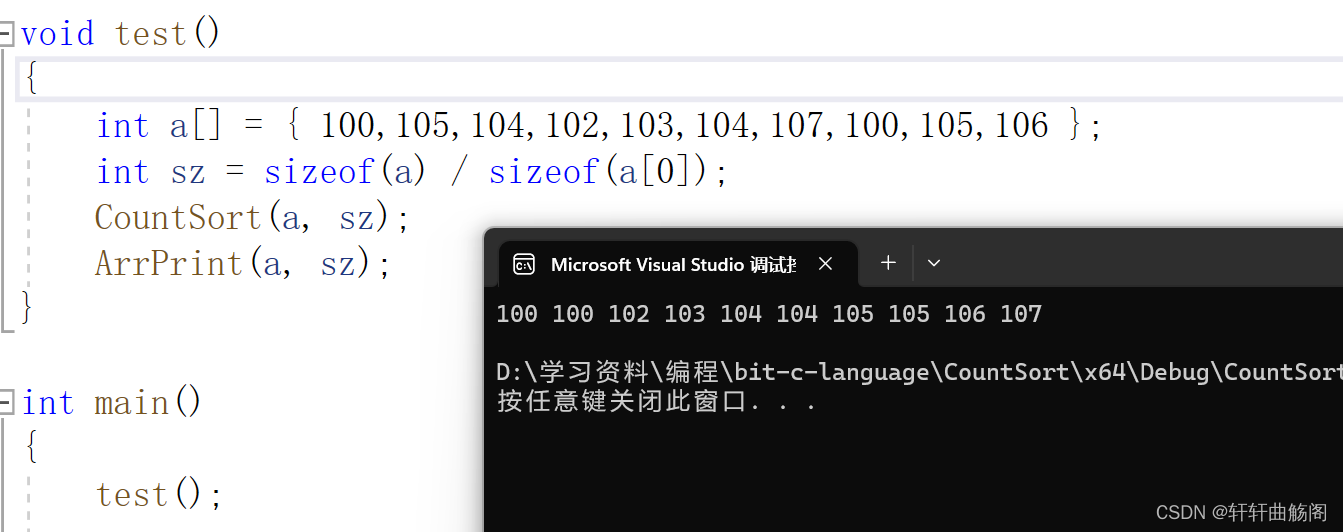
}在此,我们用下面的代码来验证
void test()
{
int a[] = { 100,105,104,102,103,104,107,100,105,106 };
int sz = sizeof(a) / sizeof(a[0]);
CountSort(a, sz);
ArrPrint(a, sz);
}
int main()
{
test();
return 0;
}有