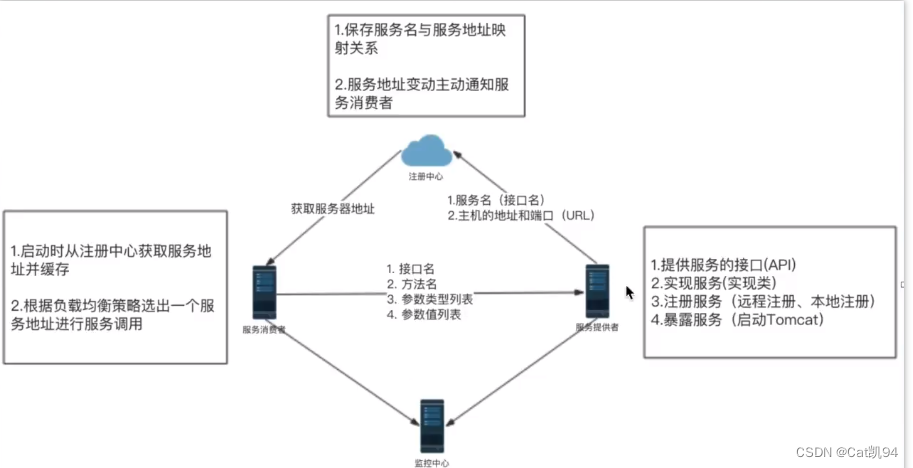
文章目录
- 前言
- 一、堆
- 1、 概念
- 2、性质
- 3、结构
- 二、堆的实现
- 1、算法实现:
- 向下调整算法
- 向上调整算法(堆的创建)
- 堆的插入
- 堆的删除
- 堆的排序
- 2、 代码实现(小堆):
- 堆的定义
- 交换
- 检查容量
- 向下调整
- 向上调整
- 堆的初始化
- 堆的创建
- 销毁堆
- 堆的插入
- 堆的删除
- 获取堆顶元素
- 判空
- 堆排序
- 打印堆
前言
基本概念:
1、完全二叉树:若二叉树的深度为h,则除第h层外,其他层的结点全部达到最大值,且第h层的所有结点都集中在左子树。
2、满二叉树:满二叉树是一种特殊的的完全二叉树,所有层的结点都是最大值。
一、堆
1、 概念
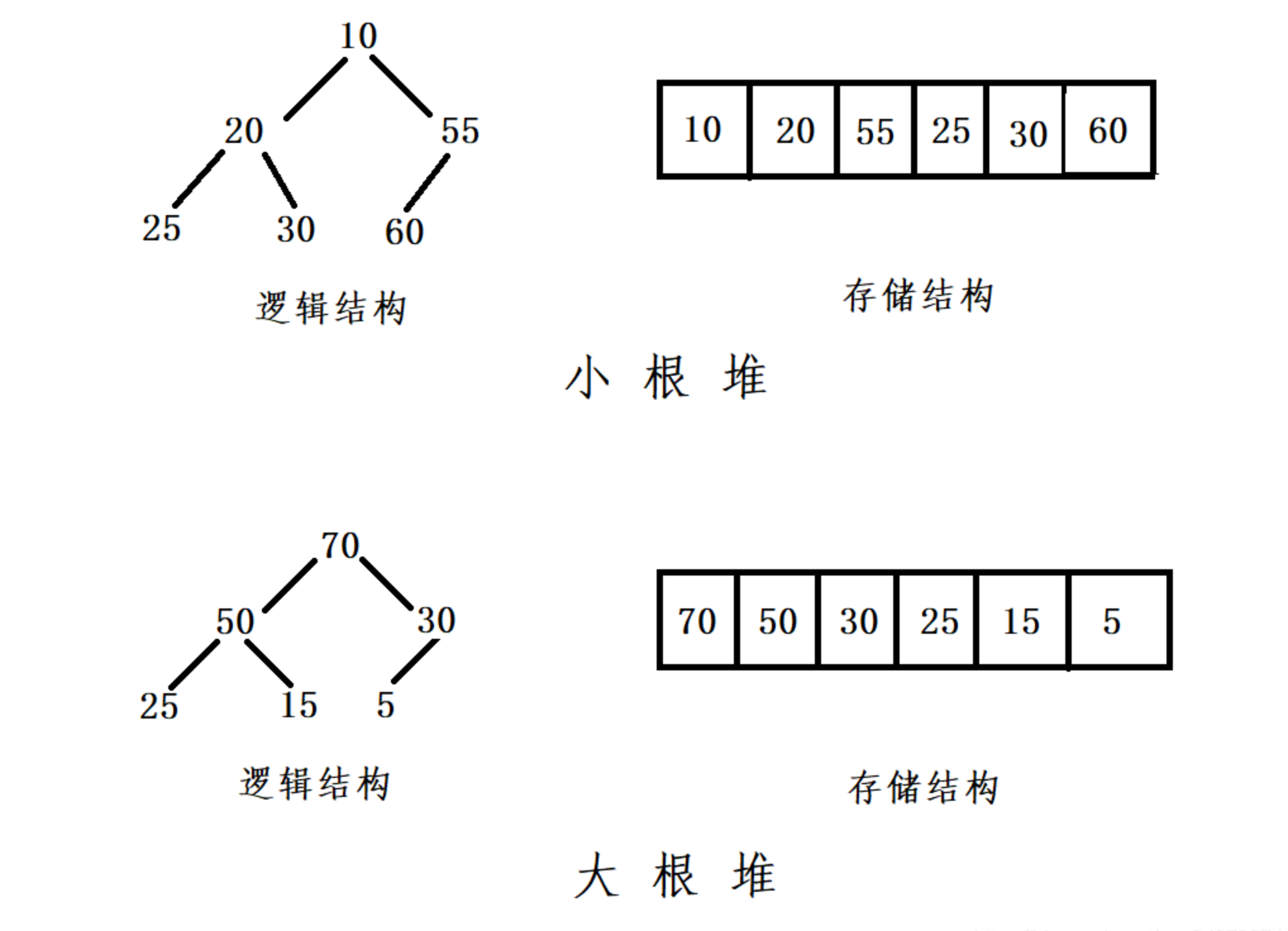
如果有一个关键码的集合K = {k0,k1, k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足:Ki <= K2i+1 且 Ki<=K2i+2 ,则称为小堆(或大堆)。
将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
2、性质
- 堆中某个节点的值总是不大于或不小于其父节点的值;
- 堆总是一棵完全二叉树。
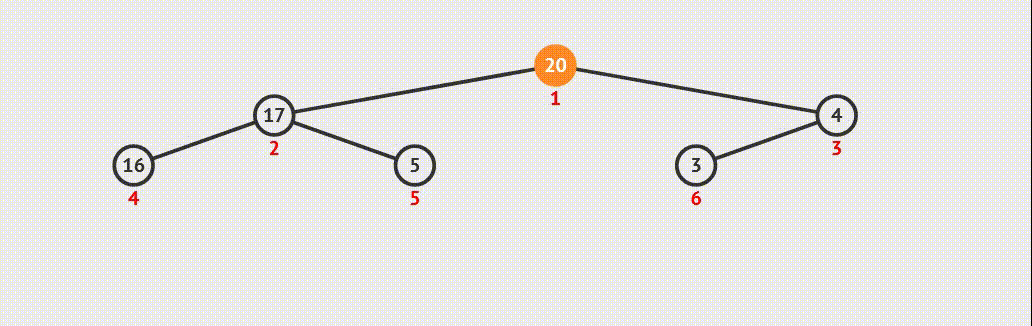
3、结构
二、堆的实现
1、算法实现:
向下调整算法
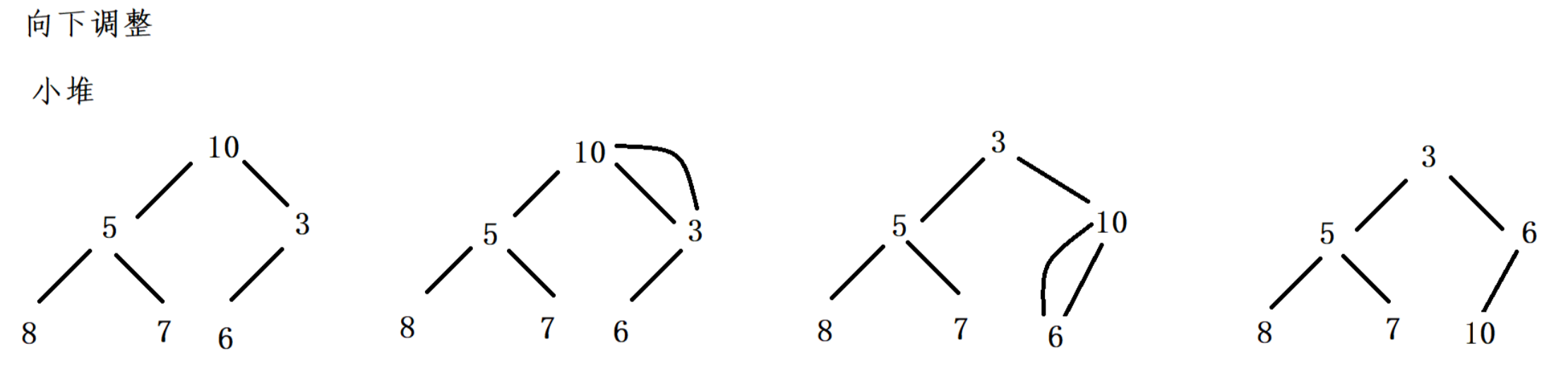
堆的向下调整:
(以小堆为例)
- 先设定根节点为当前节点(通过下标获取,标记为cur),比较左右子树的值,找出更小的值,用child来标记。
- 比较child和cur的值,如果child比cur小,则不满足小堆的规则,需要进行交换。
- 如果child比cur大,满足小堆的规则,不需要交换,调整结束。
- 处理完一个节点之后,从当前的child出发,循环之前的过程。
向下调整(小堆)示例:
向下调整(大堆)示例:
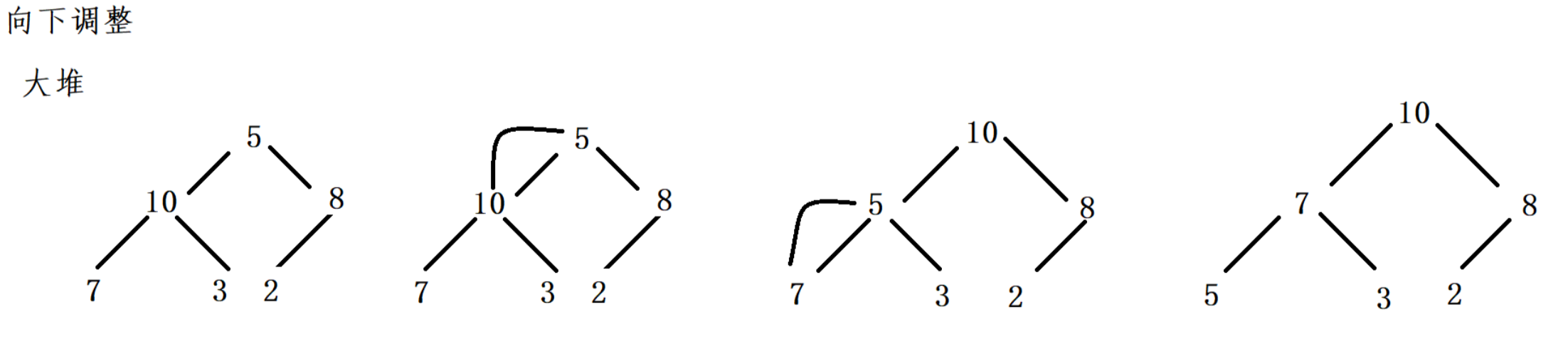
向上调整算法(堆的创建)
下面我们给出两个数组,这个数组逻辑上可以看做一颗完全二叉树,但是还不是一个堆,现在我们通过算法,把它构建成一个堆。
根节点左右子树不是堆,我们怎么调整呢?
这里我们从倒数的第一个非叶子节点的子树开始调整,一直调整到根节点的树,就可以调整成堆。
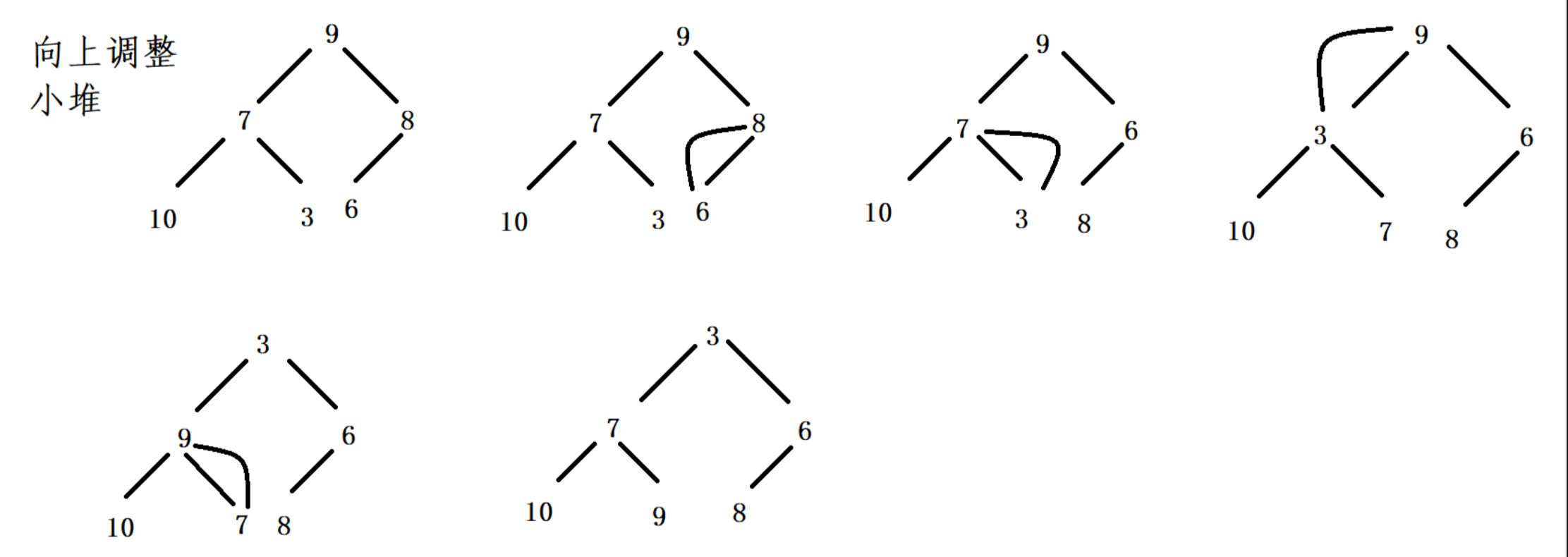
堆的向上调整:
(以小堆为例)
- 先设定倒数的第一个叶子节点为当前节点(通过下标获取,标记为cur),找出他的父亲节点,用parent来标记。
- 比较parent和cur的值,如果cur比parent小,则不满足小堆的规则,需要进行交换。
- 如果cur比parent大,满足小堆的规则,不需要交换,调整结束。
- 处理完一个节点之后,从当前的parent出发,循环之前的过程。
int a[] = {9,7,8,10,3,6}
向上调整(小堆)示例:
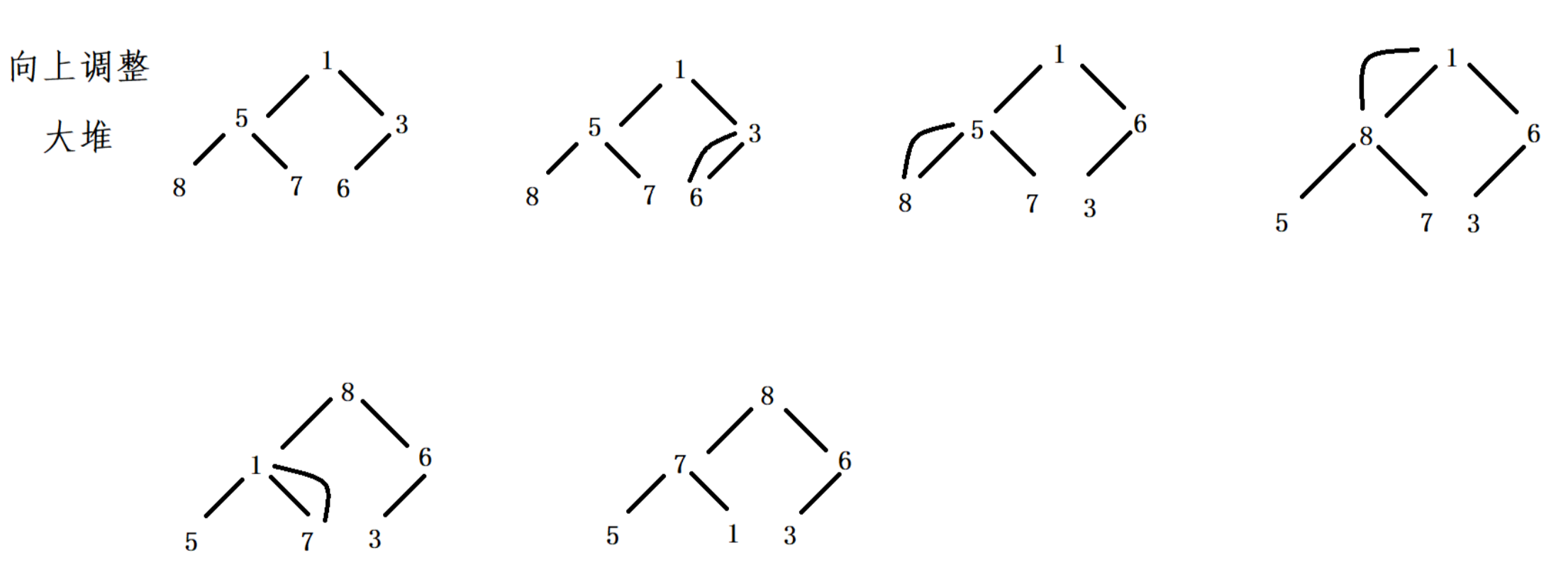
int a[] = {1,5,3,8,7,6}
向上调整(大堆)示例:
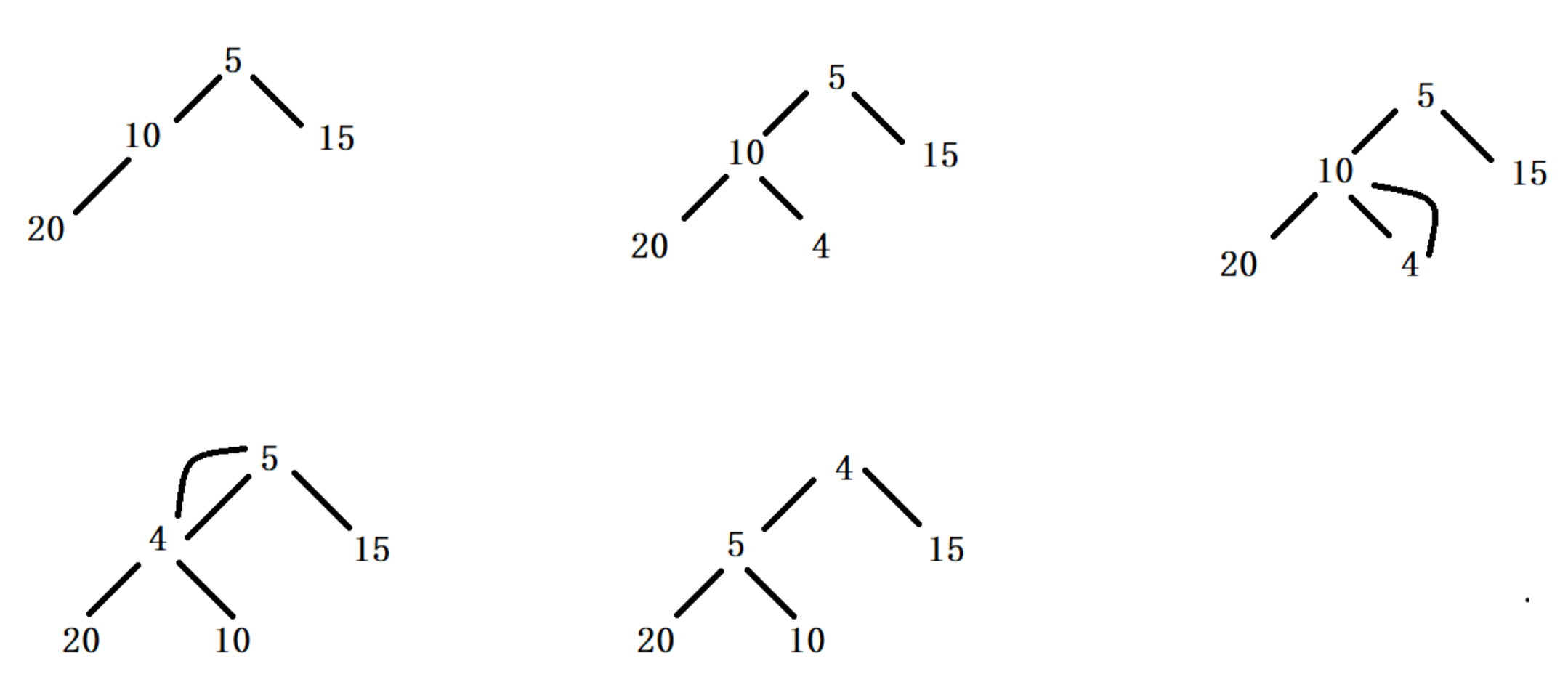
堆的插入
将数据插入到数组最后,再进行向上调整。
int a[]={5,10,15,20}
int a[]={5,10,15,20,4}
示例:
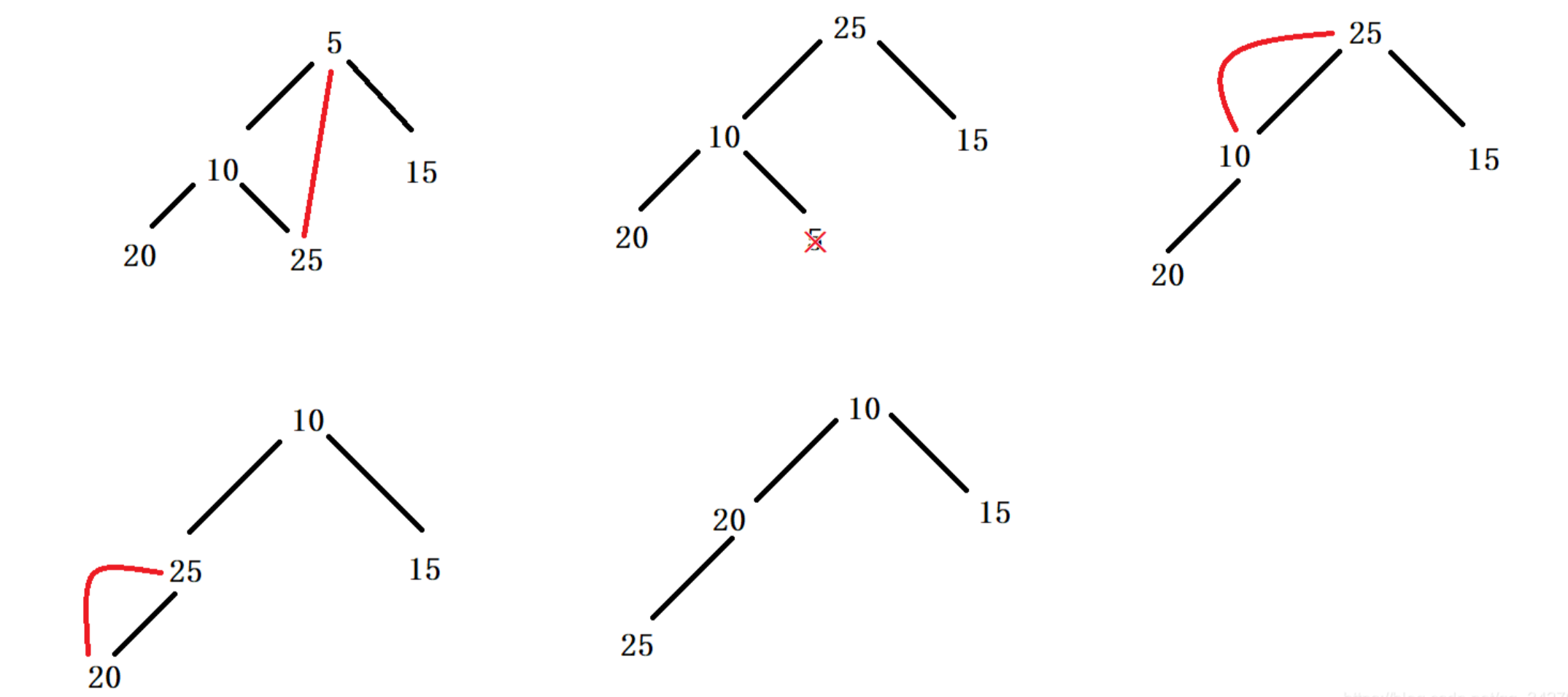
堆的删除
删除堆是删除堆顶的数据。
将堆顶的数据和最后一个数据交换,然后删除数组最后一个数据,再进行向下调整算法。
示例:
堆的排序
基本思想:
将待排序序列构造成一个大顶堆
此时,整个序列的最大值就是堆顶的根节点。
将其与末尾元素进行交换,此时末尾就为最大值。
然后将剩余n-1个元素重新构造成一个堆,这样会得到n-1个元素的次小值。如此反复执行,便能得到一个有序序列了。
动态演示:
可视化网站:数据结构和算法动态可视化
2、 代码实现(小堆):
(以小堆为示例)
堆的定义
typedef int HDataType;
typedef struct heap
{
HDataType* data;
int size;
int capacity;
}heap;
交换
void Swap(int* a, int* b)
{
int temp = *a;
*a = *b;
*b = temp;
}
检查容量
void checkCapcity(heap* hp)
{
if (hp->capacity == hp->size)
{
int newC = hp->capacity == 0 ? 1 : 2 * hp->capacity;
hp->data = (HDataType*)realloc(hp->data, sizeof(HDataType)*newC);
hp->capacity = newC;
}
}
向下调整
void shiftDown(int* arr, int n, int cur)
{
int child = 2 * cur + 1;
while (child < n)
{
//比较左右子树,找到较小值
if (child + 1 < n &&arr[child + 1]<arr[child])
{
++child;
//child时刻保存较小值的下标
}
if (arr[child] < arr[cur])
{
Swap(&arr[child], &arr[cur]);
cur = child;
child = 2 * cur + 1;
}
else
{
break;
}
}
}
向上调整
void shiftUp(int* arr, int n, int cur)
{
int parent = (cur - 1) / 2;
while (cur > 0)
{
if (arr[cur] < arr[parent])
{
Swap(&arr[cur], &arr[parent]);
cur = parent;
parent = (cur - 1) / 2;
}
else
{
break;
}
}
}
堆的初始化
void heapInit(heap* hp)
{
assert(hp);
hp->data = NULL;
hp->capacity = hp->size = 0;
}
堆的创建
void heapCreate(heap* hp, int* arr, int n)
{
assert(hp);
hp->data = (HDataType*)malloc(sizeof(HDataType)*n);
memcpy(hp->data, arr, sizeof(HDataType)*n);
hp->capacity = hp->size = n;
for (int i = (n - 2) / 2; i >= 0; i--)
{
shiftDown(hp->data, hp->size, i);
}
}
销毁堆
void heapDestory(heap* hp)
{
assert(hp);
free(hp->data);
hp->data = NULL;
hp->capacity = hp->size = 0;
}
堆的插入
void heapPush(heap* hp, HDataType val)
{
assert(hp);
checkCapcity(hp);
hp->data[hp->size++] = val;
shiftUp(hp->data, hp->size, hp->size - 1);
}
堆的删除
void heapPop(heap* hp)
{
if (hp->size > 0)
{
swap(&hp->data[0], &hp->data[hp->size - 1]);
hp->size--;
shiftDown(hp->data, hp->size, 0);
}
}
获取堆顶元素
HDataType heapTop(heap* hp)
{
assert(hp);
return hp->data[0];
}
判空
int heapEmpty(heap* hp)
{
if (hp == NULL || hp->size == 0)
{
return 1;
}
else
{
return 0;
}
}
堆排序
void heapSort(heap* hp)
{
assert(hp);
for (int i = (hp->size - 2) / 2; i >= 0; i--)
{
shiftDown(hp->data, hp->size, i);
}
int end = hp->size - 1;
while (end > 0)
{
Swap(&hp->data[0], &hp->data[end]);
shiftDown(hp->data, end, 0);
end--;
}
}
打印堆
void HeapPrint(heap* hp)
{
assert(hp);
for (int i = 0; i < hp->size; i++)
{
printf("%d ", hp->data[i]);
}
printf("\n");
}





![[算法] ArrayList 和 LinkedList 的优缺点比较及使用场景](https://img-blog.csdnimg.cn/ca65ad5cc13e426980d309780a554c60.gif)