目录
- 一、线性模型基本概念
- 二、梯度下降
- 三、反向传播
- 四、使用 Pytorch 实现线性模型
一、线性模型基本概念
线性模型: y ^ = x ∗ ω + b \hat{y} = x * \omega + b y^=x∗ω+b
简化版本,将 b b b 加入到权重矩阵 ω \omega ω 中: y ^ = x ∗ ω \hat{y} = x * \omega y^=x∗ω
单个样本的损失函数: l o s s = ( y ^ − y ) 2 = ( x ∗ ω − y ) 2 loss = (\hat{y} - y)^2 = (x * \omega - y)^2 loss=(y^−y)2=(x∗ω−y)2
整个 t r a i n i n g s e t training\ set training set 的损失函数(Mean Square Error, MSE): c o s t = 1 N ∑ n = 1 N ( y n ^ − y n ) 2 cost = \frac{1}{N} \sum_{n=1}^N (\hat{y_n} - y_n)^2 cost=N1∑n=1N(yn^−yn)2
代码实现及绘图:
import numpy as np
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
def forward(x): # 定义模型
return x * w
def loss(x, y): # 损失函数
y_pred = forward(x)
return (y_pred - y) * (y_pred - y)
w_list = []
mse_list = []
for w in np.arange(0.0, 4.1, 0.1):
print('w=', w)
l_sum = 0
for x_val, y_val in zip(x_data, y_data):
y_pred_val = forward(x_val)
loss_val = loss(x_val, y_val)
l_sum += loss_val
print('\t', x_val, y_val, y_pred_val, loss_val)
print('MSE=', l_sum / 3)
w_list.append(w)
mse_list.append(l_sum / 3)
plt.plot(w_list, mse_list)
plt.ylabel('loss')
plt.xlabel('w')
plt.show()
二、梯度下降
损失函数 MSE: c o s t = 1 N ∑ n = 1 N ( y n ^ − y n ) 2 cost = \frac{1}{N} \sum_{n=1}^N (\hat{y_n} - y_n)^2 cost=N1∑n=1N(yn^−yn)2
为了使损失函数最小,即需要找到一个 ω ∗ \omega^* ω∗ 使得 c o s t cost cost 值最小: ω ∗ = a r g m i n c o s t ( ω ) ω \omega^* = \underset{\omega} {arg \ min \ cost(\omega)} ω∗=ωarg min cost(ω)
梯度: G r a d i e n t = ∂ c o s t ∂ ω = ∂ ∂ ω 1 N ∑ n = 1 N ( x n ⋅ ω − y n ) 2 = 1 N ∑ n = 1 N ∂ ∂ ω ( x n ⋅ ω − y n ) 2 = 1 N ∑ n = 1 N 2 ⋅ ( x n ⋅ ω − y n ) ∂ ( x n ⋅ ω − y n ) ∂ ω = 1 N ∑ n = 1 N 2 ⋅ x n ⋅ ( x n ⋅ ω − y n ) \begin{aligned} Gradient &= \frac{\partial cost}{\partial \omega} \\ &= \frac{\partial}{\partial \omega} \frac{1}{N} \sum^N_{n=1} (x_n \cdot\ \omega - y_n)^2 \\ &= \frac{1}{N} \sum_{n=1}^N \frac{\partial}{\partial \omega} (x_n \cdot \ \omega - y_n)^2 \\ &= \frac{1}{N} \sum_{n=1}^N 2 \cdot \ (x_n \cdot \ \omega - y_n) \frac{\partial (x_n \cdot \ \omega - y_n)}{\partial \omega} \\ &= \frac{1}{N} \sum_{n=1}^N 2 \cdot \ x_n \cdot \ (x_n \cdot \ \omega - y_n) \end{aligned} Gradient=∂ω∂cost=∂ω∂N1n=1∑N(xn⋅ ω−yn)2=N1n=1∑N∂ω∂(xn⋅ ω−yn)2=N1n=1∑N2⋅ (xn⋅ ω−yn)∂ω∂(xn⋅ ω−yn)=N1n=1∑N2⋅ xn⋅ (xn⋅ ω−yn)
梯度更新: ω = ω − α ∂ c o s t ∂ ω = ω − α 1 N ∑ n = 1 N 2 ⋅ x n ⋅ ( x n ⋅ ω − y n ) \begin{aligned} \omega &= \omega - \alpha \frac{\partial cost}{\partial \omega} \\ &= \omega - \alpha \frac{1}{N} \sum_{n=1}^N 2 \cdot x_n \cdot \ (x_n \cdot \ \omega - y_n) \end{aligned} ω=ω−α∂ω∂cost=ω−αN1n=1∑N2⋅xn⋅ (xn⋅ ω−yn)
代码实现:
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = 1.0
def forward(x):
return x * w
def cost(xs, ys):
cost = 0
for x, y in zip(xs, ys):
y_pred = forward(x)
cost += (y_pred - y) ** 2
return cost / len(xs)
def gradinet(xs, ys):
grad = 0
for x, y in zip(xs, ys):
grad += 2 * x * (x * w - y)
return grad / len(xs)
print('Predict (before training)', 4, forward(4))
Epoch_list = []
loss_list = []
for epoch in range(100):
cost_val = cost(x_data, y_data)
grad_val = gradinet(x_data, y_data)
w -= 0.01 * grad_val
Epoch_list.append(epoch)
loss_list.append(cost_val)
print('Epoch:', epoch, 'w=', w, 'loss=', cost_val)
print('Predict (after training)', 4, forward(4))
plt.plot(Epoch_list, loss_list)
plt.xlabel('Epoch')
plt.ylabel('cost')
plt.show()
随机梯度下降(Stochastic Gradient Desce,SGD),多指 mini-batch 的随机梯度下降。
三、反向传播
首先了解计算图,对于一个两层的神经网络模型:
y
^
=
W
2
(
W
1
⋅
X
+
b
1
)
+
b
2
=
W
2
⋅
W
1
⋅
X
+
(
W
2
b
1
+
b
2
)
=
W
⋅
X
+
b
\begin{aligned} \hat{y} &= W_2(W_1 \cdot X + b_1) + b_2 \\ &= W_2 \cdot W_1 \cdot X + (W_2b_1 + b_2) \\ &= W \cdot X + b\\ \end{aligned}
y^=W2(W1⋅X+b1)+b2=W2⋅W1⋅X+(W2b1+b2)=W⋅X+b对于这个模型,可以构建计算图如下: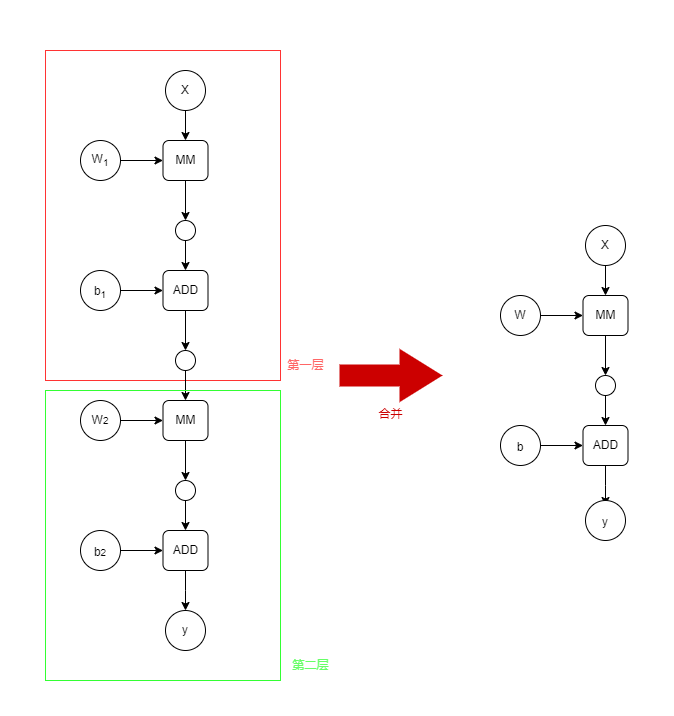
由上式可以知道,不管多少层的一个线性的神经网络模型,都可以化简为一个仅包含一层的神经网络模型,这样的话,那些设计多个隐藏层的神经网络模型就没有意义了。所以在每一层的结尾都需要一个非线性函数,改进后的模型如下,其中
σ
\sigma
σ 表示一个非线性函数。
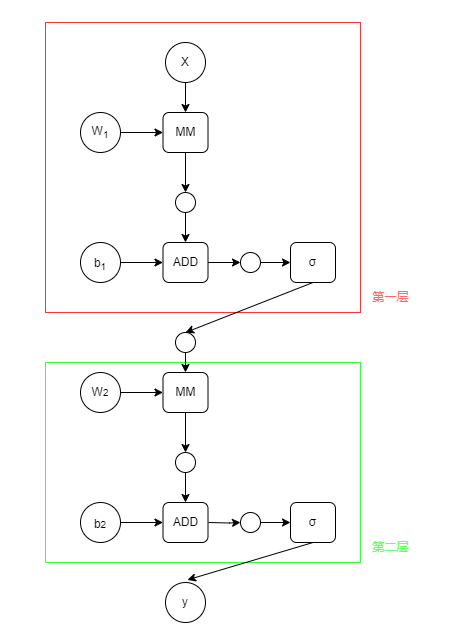
课程中这里有对链式求导法则的讲解,但是那个很简单,这里就跳过了。
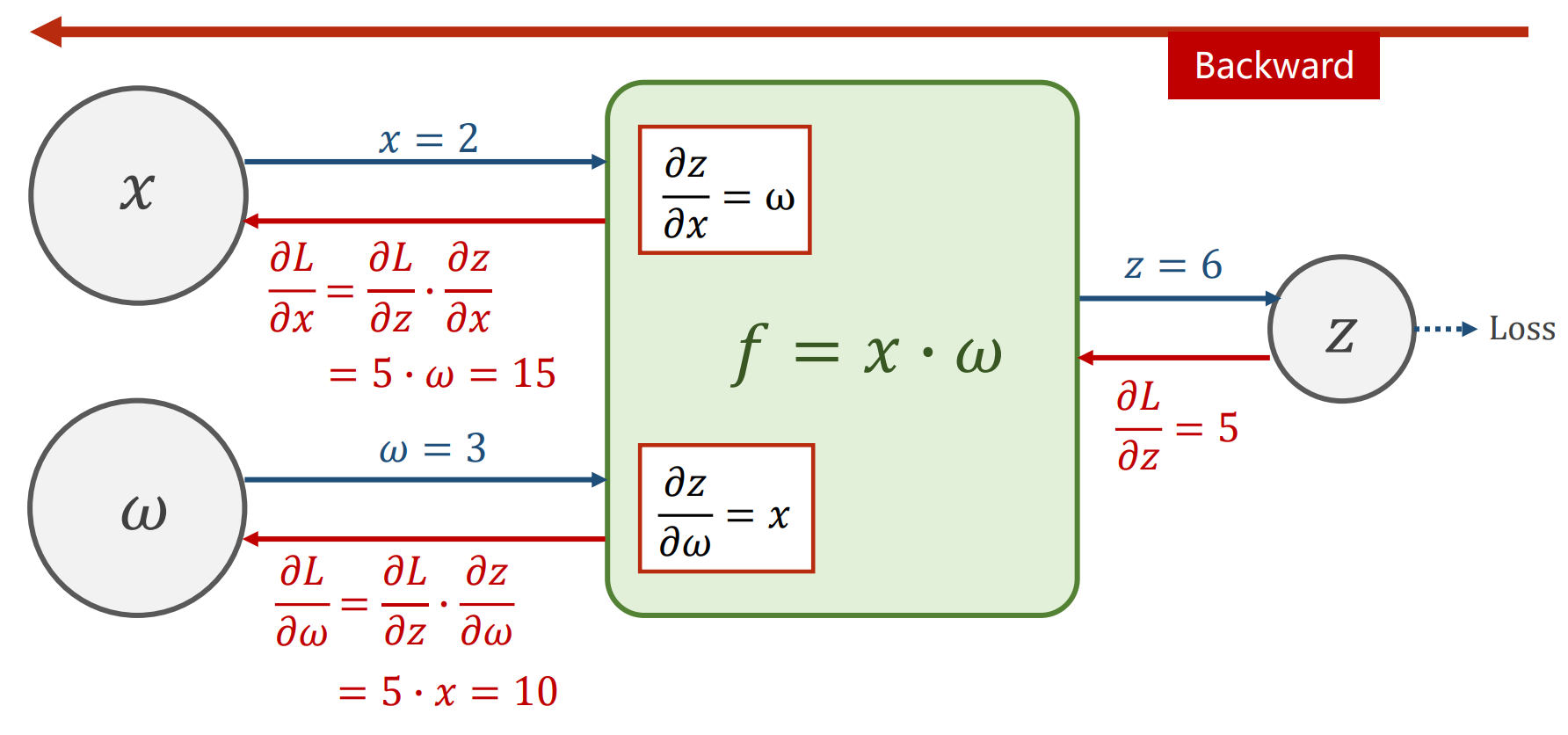
有了计算图,就可以开始了解传播算法了。下面是一个例子,先进性前馈传播,再进行反向传播,虽然在 Pytorch 这样的框架里面实现了自动求解梯度的功能,但是下面的两张图是原理的解释。
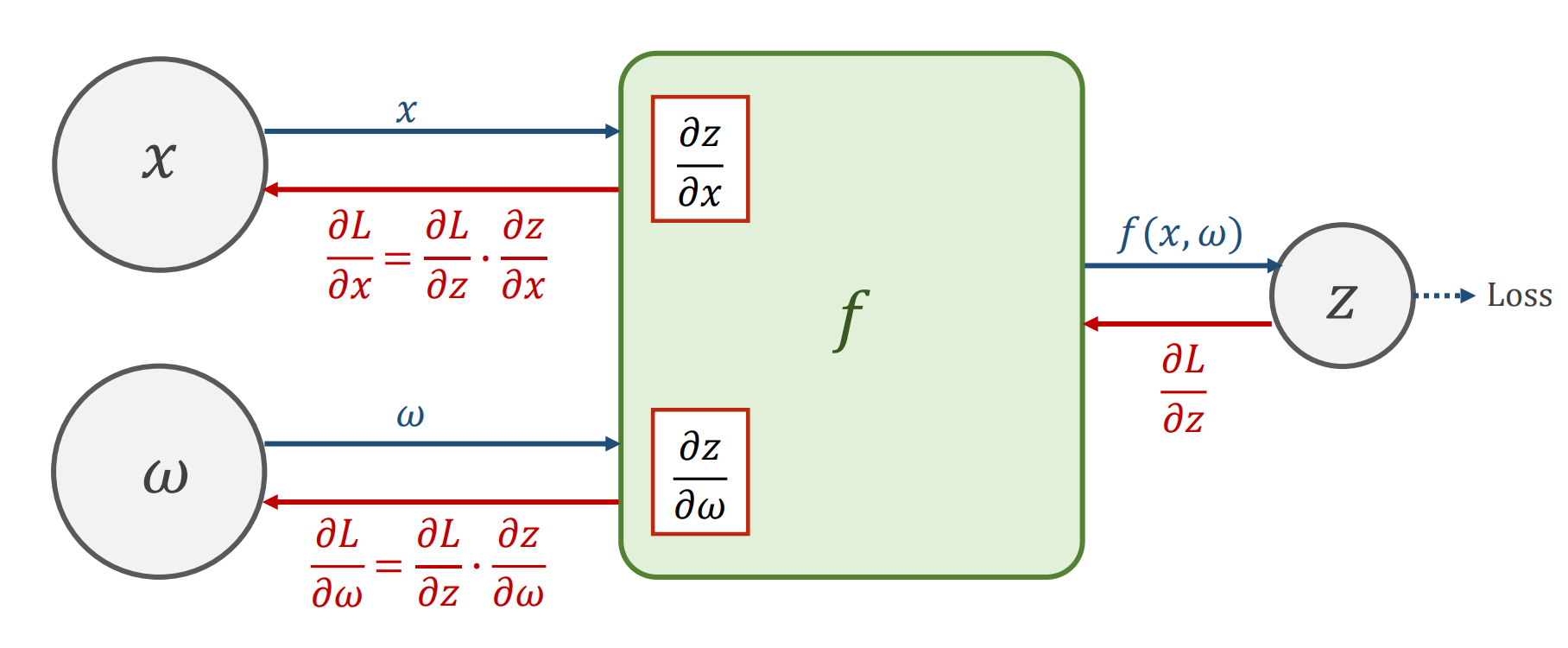
下面是一个计算的实例:
下面使用 Pytorch 实现一下传播算法。
注意,在 Pytorch 中的一个基本单位是张量(Tensor),它可以用于动态创建计算图,其中包含数据(data)以及损失函数对于该张量(一般是指权重)的梯度(grad)。
import torch
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
# 创建一个张量并且需要自动计算梯度
w = torch.Tensor([1.0])
w.requires_grad = True
# 构建计算图
def forward(x):
return x * w # 注意这里计算的时候x也被转换为了张量
def loss(x, y):
y_pred = forward(x)
return (y_pred - y) ** 2
print('predict (before training)', 4, forward(4).item())
epoch_list = []
l_list = []
for epoch in range(100):
for x, y in zip(x_data, y_data):
l = loss(x, y)
l.backward()
epoch_list.append(epoch)
l_list.append(l.item())
print('\tgrad:', x, y, w.grad.item())
w.data = w.data - 0.01 * w.grad.data
w.grad.data.zero_() # 梯度置零,否则会累加
print('progress:', epoch, l.item())
print('predict (after training)', 4, forward(4).item())
plt.plot(epoch_list, l_list)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
四、使用 Pytorch 实现线性模型
import torch
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[2.0], [4.0], [6.0]])
class LinearModel(torch.nn.Module):
def __init__(self):
super(LinearModel, self).__init__() # 调用父类的构造函数
self.linear = torch.nn.Linear(1, 1) # 权重和偏置值的维度feature
def forward(self, x):
y_pred = self.linear(x) # 对象后面接参数,调用了__call__()方法
return y_pred
model = LinearModel()
criterion = torch.nn.MSELoss(reduction='sum') # 损失函数
optimizer = torch.optim.SGD(model.parameters(), lr=0.01) # 优化方法:梯度下降
for epoch in range(1000):
y_pred = model(x_data) # forward,调用了__call__()方法
loss = criterion(y_pred, y_data)
print(epoch, loss.item())
optimizer.zero_grad() # 梯度置零
loss.backward()
optimizer.step() # 更新梯度
print('w=', model.linear.weight.item())
print('b=', model.linear.bias.item())
x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print('y_pred=', y_test.item())