文章目录
- 函数
- 判断函数的条件
- 复合函数
- 复合函数的性质
- 逆函数
函数

判断函数的条件
dom F = A
⇔
\Leftrightarrow
⇔所有x 都有 F(x)与之对应
有唯一的与其对应
<
x
,
y
>
∈
f
∧
<
y
,
z
>
∈
f
⇒
y
=
z
<x,y>\in f \land <y,z>\in f \Rightarrow y =z
<x,y>∈f∧<y,z>∈f⇒y=z



|A| = m (基数) ,|B|=n (m,n 不全为0)
|
B
A
B^A
BA|=
n
m
n^m
nm

单射
⇔
入射
\Leftrightarrow 入射
⇔入射 (一一对应)(
f
(
x
1
)
=
f
(
x
2
)
⇒
x
1
=
x
2
f(x1)=f(x2) \Rightarrow x1=x2
f(x1)=f(x2)⇒x1=x2)
值域全包含—>满射
y
∈
B
⇒
∃
x
(
x
∈
A
∧
y
=
f
(
x
)
)
y\in B\Rightarrow \exists x(x\in A \land y = f(x))
y∈B⇒∃x(x∈A∧y=f(x))
单射+满射=双射


不是函数



复合函数


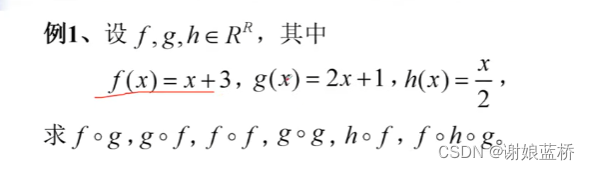


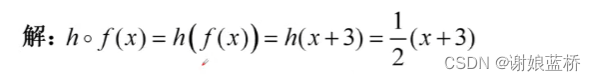
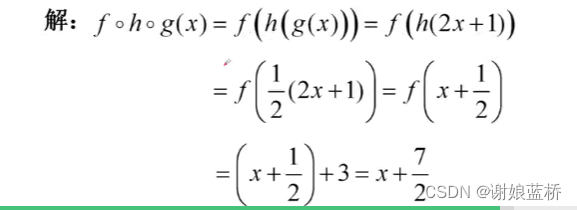
复合函数的性质


逆函数
函数不一定存在逆函数
如果函数双射,则存在逆函数










![NSSCTF-[深育杯 2021]Press](https://img-blog.csdnimg.cn/ffcac2e9d6e242abbd0e972387bbe105.png)