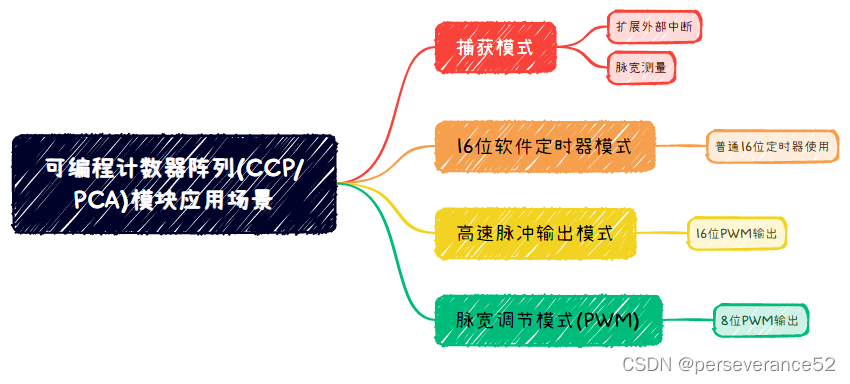
毫米波雷达系列 | 传统CFAR检测（有序统计类）

1.OS-CFAR

有序统计类CFAR检测器(OS-CFAR)与均值类CFAR检测器处理过程不同,在对背景杂波功率进行估计时，需要将所有参考单元进行升序排列得到一个新的有序数列，在新序列中选取第k个值作为背景杂波功率值，所以带检测单元的计算表达式为：
$$Zos=X_k$$
门限因子为k，门限值S:
$$S=kZos=k{x}_k$$
相较于均值类CFAR检测器来说，OS-CFAR检测器多了一个参数k，k的取值范围一般在1/2~3/4之间。

2.TM-CFAR

剔除平均（trimmed-mean）检测器在OS-CFAR检测器基础上，又剔除了r1个最小单元和r2个最大单元，对剩余的参考单元取均值作为杂波背景估计：
$$Ztm=\sum _{i=r1+1}^{N-r2}{x}_i$$
门限值S:
$$S=kZtm=k\sum _{i=r1+1}^{N-r2}{x}_i$$

3.仿真对比

在均匀杂波环境、多目标环境和杂波边缘环境中对均值类CFAR检测器的性能进行比较分析。

参数设置：

虚警概率	10-4
参考单元	32
保护单元	4
信噪比SNR	20
多目标单元位置	110和120
比例系数	3/4
r1、r2	2、4
杂波边缘功率	20dB、30dB

（1）均匀环境

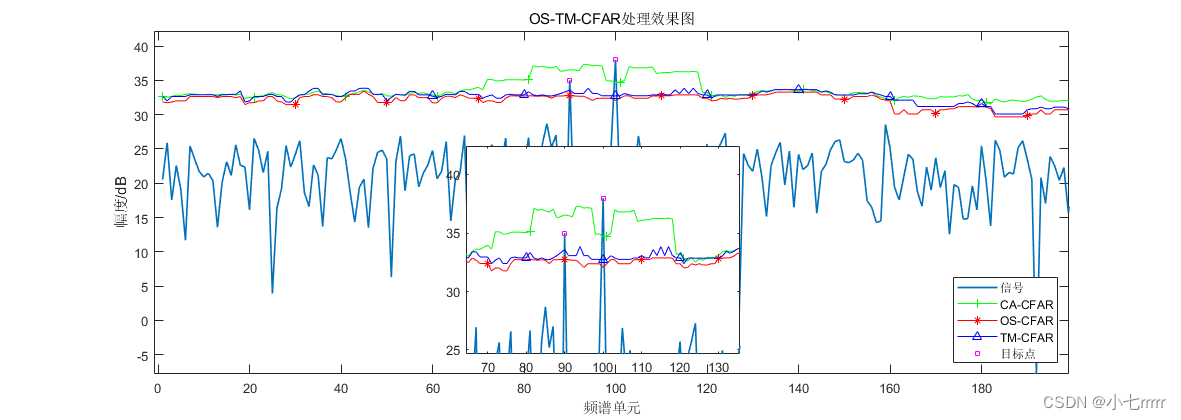
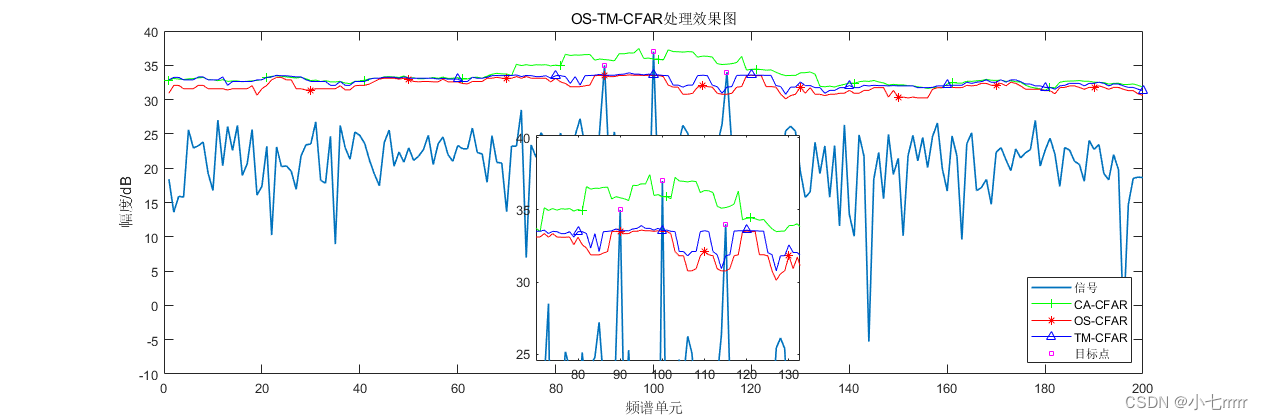
（2）多目标

（3）杂波边缘

从结果图中可以看出，在均匀环境中三种检测器均在第80个距离单元处检测到目标，在均匀环境中有序统计类CFAR检测器和CA-CFAR检测器一样具有良好的检测性能；在存在两个目标的环境中，只有CA-CFAR检测器发生漏警，OS-CFAR和TM-CFAR均可以检测出全部目标，并且OS-CFAR门限值更加平缓，说明在多目标环境中有序统计类CFAR检测器依旧表现出优异的检测性能。当存在三个目标时，OS-CFAR和TM-CFAR都可以检测出所有目标，而CA-CFAR仍然存在目标遮蔽现象，可以得知有序统计类CFAR检测器在多目标环境中的优势是均值类CFAR检测器无法比拟的；统计有序类CFAR检测器在边缘杂波环境下的虚警控制能力一般，在杂波边缘高功率附近容易发生虚警现象。

（4）代码

OS-CFAR

function [ XT ] = cfar_os( xc, N, k, pro_N, PAD)
%   假设回波服从高斯分布
%   alpha赋值有些问题，一个比较复杂的高次函数

%% 计算alpha
% syms alpha PFA;
% PFA(alpha)=gamma(N-1).*gamma(N-k+alpha-1)./gamma(N-k-1)./gamma(N+alpha-1);
% [alpha,~,~]=solve(PFA(alpha)==PAD,'ReturnConditions', true) ;

alpha=N.*(PAD.^(-1./N)-1);
persistent left; %类似于Java中静态变量
persistent right;
persistent HalfSlide;
persistent HalfProt;
persistent len;
persistent Ksite;
if isempty(left)
    HalfSlide=N/2;
    HalfProt=pro_N/2;
    left=1+HalfProt+HalfSlide;                              % 左边界
    right=length(xc)-HalfProt-HalfSlide;                    % 右边界
    len=length(xc);
    Ksite=round(N*k);
end
XT=zeros(1,len); %检测阈值

for i=1:left-1  %左边界
    cell_right=xc(1,i+HalfProt+1:i+HalfSlide*2+HalfProt);
    cell_right=sort(cell_right);
    XT(1,i)=cell_right(Ksite)*alpha;
end

for i=left:right    %中间区域
    cell_left=xc(1,i-HalfSlide-HalfProt:i-HalfProt-1);
    cell_right=xc(1,i+HalfProt+1:i+HalfSlide+HalfProt);
    cell=sort([cell_left,cell_right]);
    XT(1,i)=cell(Ksite)*alpha;
end

for i=right+1:len    %右边界
    cell_left=xc(1,i-HalfSlide*2-HalfProt:i);
    cell_left=sort(cell_left);
    XT(1,i)=cell_left(Ksite)*alpha;
end    
end

TM-CFAR

function [ XT ] = cfar_tm( xc, N, k, pro_N, PAD,r1,r2)
%   假设回波服从高斯分布
%   alpha赋值有些问题，一个比较复杂的高次函数
alpha=N.*(PAD.^(-1./N)-1);

persistent left; %类似于Java中静态变量
persistent right;
persistent HalfSlide;
persistent HalfProt;
persistent len;
persistent Ksite;
if isempty(left)
    HalfSlide=N/2;
    HalfProt=pro_N/2;
    left=1+HalfProt+HalfSlide;                              % 左边界
    right=length(xc)-HalfProt-HalfSlide;                    % 右边界
    len=length(xc);
    Ksite=round(N*k);
end
XT=zeros(1,len); %检测阈值

for i=1:left-1  %左边界
    cell_right=xc(1,i+HalfProt+1:i+HalfSlide*2+HalfProt);
    cell_right=sort(cell_right);
    cell_r=cell_right(1+r1:end-r2);
    XT(1,i)=cell_r(Ksite)*alpha;
end

for i=left:right    %中间区域
    cell_left=xc(1,i-HalfSlide-HalfProt:i-HalfProt-1);
    cell_right=xc(1,i+HalfProt+1:i+HalfSlide+HalfProt);
    cell=sort([cell_left,cell_right]);
    cell_r=cell(1+r1:end-r2);
    XT(1,i)=cell_r(Ksite)*alpha;
end

for i=right+1:len    %右边界
    cell_left=xc(1,i-HalfSlide*2-HalfProt:i);
    cell_left=sort(cell_left);
    cell_r=cell_left(1+r1:end-r2);
    XT(1,i)=cell_r(Ksite)*alpha;
end    
end