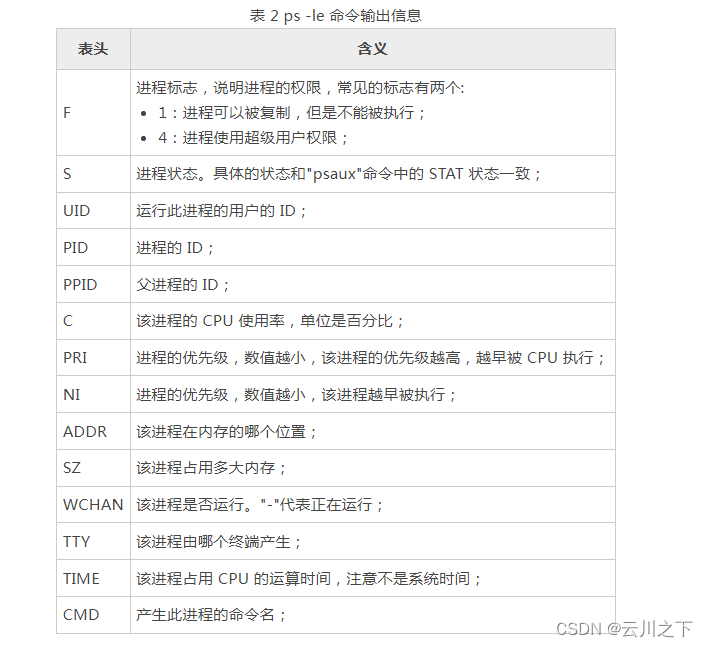
图有两种遍历方式：DFS深度优先，BFS广度优先。

把所有顶点访问一遍，且每个顶点只访问一次，把走过的顶点标记一下。

标记：为图设置一个访问标志数组visited[n］，用于标示图中每个顶点是否被访问过，它的初始值为0(“假”)，表示顶点均未被访问；一旦访问过顶点vi，则置访问标志数组中的visited[i]1(“真”)，以表示该顶点已访问。

深度优先遍历：顺着一条路走，若走到相邻的顶点都遍历过了——回溯看上一个顶点是否还有未访问的邻接顶点。

图1 图的深度优先遍历 

 广度优先遍历：从一个顶点开始走，先走完它所有的邻接顶点，然后再走其邻接顶点的邻接顶点（与树的层遍历相似）。

 图2 图的广度优先遍历

---

BFS广度优先

        广度优先跟树的层遍历相似，都要用到队列。

void GraphLink::BFS(char v)//广度优先
{
	int p = GetVertexIndex(v);//获取改顶点的下标
	if (p == -1)return;
	bool* visited = new bool[m_NumVertex];//标记每个点是否访问
	for (int i = 0; i < m_NumVertex; i++)//一开始都置为假-没有被访问过
		visited[i] = false;

	queue<char> qq;
	qq.push(p);//入队
	visited[p] = true;//被访问-真
	cout << v << " ";//输出
	int front;
	Edge* plist = nullptr;
	while (!qq.empty())
	{
		front = qq.front();//得到队头（下标）
		qq.pop();//出队
		plist = m_VerArr[front].m_list;//指向那个头的list（邻接顶点链表）
		while (plist != nullptr)//有邻接顶点
		{
			if (!visited[plist->m_destindex])//没被访问过
			{
				cout << m_VerArr[plist->m_destindex].m_VerValue << " ";//输出
				visited[plist->m_destindex] = true;//访问了
				qq.push(plist->m_destindex);//放到队列里
			}
			plist = plist->m_next;//指向下一个邻接顶点下标
		}
	}
	cout << endl;
    delete[]visited;
	visited = nullptr;
}

 建立这样的图

 广度优先：

---

 DFS深度优先 

        深度优先会使用递归和回溯，但是是否被访问visited数组应该是同一的，不因递归重置，所以深度优先可以写两个函数，一个创建visited，然后把数组传入另一个函数。

void GraphLink::DFS(int v, bool* visited)
{
	cout << m_VerArr[v].m_VerValue << " ";//遍历到
	visited[v]=true;//置为真
	Edge* plist = m_VerArr[v].m_list;//指向其邻接顶点链表
	while (plist != nullptr)
	{
		if (!visited[plist->m_destindex])//没有被访问过
		{
			DFS(plist->m_destindex, visited);//继续深度优先
		}//都访问了，回溯
		plist = plist->m_next;指向下一个邻接顶点
	}
}
void GraphLink::DFS(char v)//深度优先
{
	int p = GetVertexIndex(v);
	if (p == -1)return;
	bool* visited = new bool[m_NumVertex];
	for (int i = 0; i < m_NumVertex; i++)
		visited[i] = false;
	DFS(p, visited);//visited不能递归
	delete[] visited;
	visited = nullptr;
}

以上图用邻接表表示，邻接表创建方法见：

【图】邻接表_曦樂～的博客-CSDN博客