高等数学基础概念的Python开发实现

news2025/10/31 19:07:08

一般的数学算式math函数库就可以解决了，如果是涉及到高等数学极限，微积分等知识，就需要用到sympy科学计算库，它是专门用来解决数学的运算问题的。

Sympy是一个符号计算的Python库。它的目标是成为一个全功能的计算机代数系统，同时保持代码简洁、易于理解和扩展。它完全由Python写成，不依赖于外部库。SymPy支持符号计算、高精度计算、模式匹配、绘图、解方程、微积分、组合数学、离散数学、几何学、概率与统计、物理学等方面的功能。

官方文档：SymPy 1.11 documentation

安装 sympy：
# 第一种
pip install sympy
# 第二种推荐，镜像下载更快
pip install sympy -i Simple Index

使用 jupyter 显示效果更好。Project Jupyter | Home

导入库的方式为 from sympy import *

常见的数学符号在sympy中的表示方式：

数学符号	sympy表达	数学符号	sympy表达
sinx	sin(x)	arccosx	acos(x)
cosx	cos(x)	arcsinx	asin(x)
tanx	tan(x)	imaginary number i	I(大写i)
$e^{x}$	exp(x) 或者 E**x	$\propto$	oo(两个o)
$y^{x}$	y**x	linx	log(x)
$\frac{x}{y}$	x/y	$\pi$	pi

基本数学方法

from sympy import * # 导入sympy 全部函数
#数学表达式，用到symbols() 声明数学符号
x, y = symbols('x, y') # symbols() 声明了两个符号x, y。否则就会报 x 未定义错误
expr = x + 2*y # 定义了表达式：x + 2y
expr # x + 2*y
#可以对表达式进行简单的四则运算
expr = expr + x + 1 # 表达式可以进行基本运算
expr # 2*x + 2*y + 1
expr = expr * x + 2 # 相当于：(2*x + 2*y + 1) * x + 2
expr # x*(2*x + 2*y + 1), 并没有进行展开计算
#表达式展开成最终形式，用到 expand() 函数
expanded_expr = expand(expr)
expanded_expr # 2*x**2 + 2*x*y + x，表达式以最终能够展开的形式显示
#平方根
sqrt(8) # $2\sqrt{2}$
#如果想求8的算数平方根的具体的值，就需要用的 math 类
import math
math.sqrt(8) # 2.82842712474619
#简化表达式，用到simplify()函数
expr = (3*x**2+9)/3
expr # $p^{2}+3$
#分解因式，用到 factor() 函数
expr = factor(expanded_expr) #expanded_expr = 2*x**2 + 2*x*y + x
expr # 𝑥(2𝑥+2𝑦+1)
#解方程，用到solve(equation, symbol)，equation为等式或者表达式，symbol声明的符号即变量
x = Symbol("x")
expression = x**2+3*x-4 # 即方程 $x^{2} + 3x - 4 = 0$ ，x为变量
solve(expression, x) # 方程的解有两个：[-4,1]
solve(x**2 - 2, x) # $x^{2}$ 的解为： $[-\sqrt{2},\sqrt{2}]$
#替代变量为具体值，用到expression.subs(symbol, constant)，equation为等式或者表达式，symbol为要替换的变量，constant具体的数值
expression = x**2+3*x-4
expression.subs(x, 3) #将表达式expression中的x的值替换为3，结果为：14

高等数学方法

#求极限，用到limit(expr, symbol, value)，expr表达式，symbol变量，value变量的值
limit(x**2, x, 5) # $x^{2}$ 在点5处的极限值为 25
limit(x**3, x, oo) # $x^{3}$ 在点正 $\propto$ 处的极限值为 $\propto$
limit(1/x, x, 0) # 1/x 从正方向逼近0时的极限值为 $\propto$
limit(1/x, x, 0, dir="-") #1/x 从负方向逼近0时的极限值为 - $\propto$
limit(1/x, x, 0, dir='+-') #1/x 从正负方向逼近0时的极限值为 $\propto$
limit(sin(x)/x, x, 0) #计算 $limit_{x \to 0} \frac{sin(x)}{x}$ 的极限值为1
#计算阶乘，用到factorial()
factorial(5) #计算5的阶乘，即5×4×3×2×1=120
#求一阶导数，用到diff(expr)，计算表达式的导数
x = Symbol('x') #声明变量
expression = x**3 + x**2 + 9*x #要求导的表达式 $x^{3}+x^{2}+9x+1$
diff(expression) #求导结果： $3x^{2}+2x+9$
diff(sin(x)) #求导结果：cos(x)
diff(x**3*y*z,x) #表达式 $x^{3}yz$ 对x求导，结果为： $3x^{2}yz$
expr = x**4+x**3+x+1
expr.diff(x) #导数为： $4x^{3}+3x^{2}+1$ $4x^{3}+3x^{2}+1$
#求高阶导数
expr=sin(x)
expr.diff(x,4) #求sin(x)的4阶导数，为：sin(x)
expr=x**5 + x**4
expr.diff(x,3) #求 $x^{5}+x^{4}$ 的3阶导数，为：12x(5x+2)
#求不定积分，用到Integrate(expr)，求表达式的不定积分，即计算∫ expr dx
expr = 3*x**2 + 2*x + 9 # 表达式 $3x^{2}+2x+9$
integrate(3 * x ** 2 + 2 * x + 9) #积分为： $x^{3}+x^{2}+9x$
integrate(x*y, x) #表达式xy对x进行积分，结果为 $x^{2}y/2$
integrate(sin(x**2), (x, -oo, oo)) #计算 $\int_{-\infty }^{\infty } sin(x^{2})dx$ 积分，结果为 $\sqrt{2\pi }/2$
#求定积分，用到Integrate(expr, (x, a,b ))，求表达式的定积分，即计算 $\int_{a}^{b} exprdx$
integrate(log(x), (x, 1, a)) #log(x)对x从1到a求积分，结果为alog(a)-a+1
#二重积分，用到integrate(expr,x,y)，对表达式expr进行对x，y的二重积分。
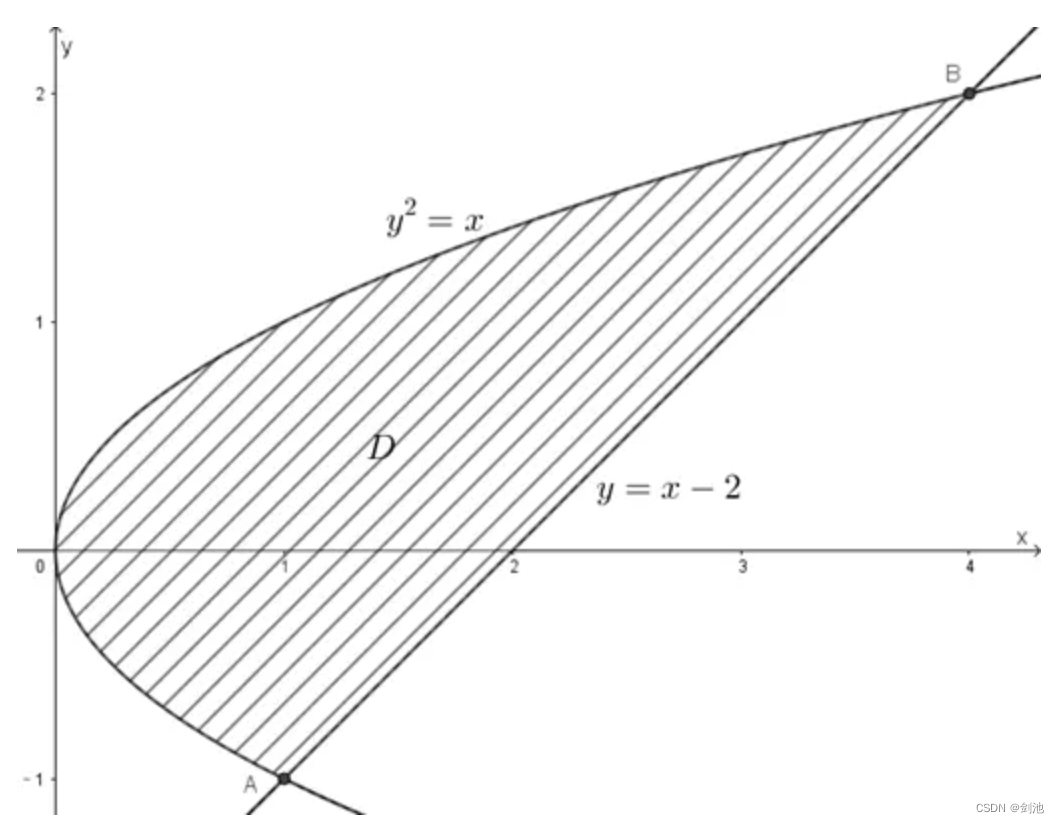
# 计算 $\int_{y^{2}}^{y+2}\int_{-1}^{2}xydxdy$ ，即计算 xy在抛物线 $y^{2} = x$ 与直线 y=x−2 所围成的区域上的二重积分
expr=x*y # 表达式
integrate(expr,(x, y**2,y+2),(y,-1,2)) # y区间[-1,2]，x区间[y**2, y+2]，结果: 45/8
附图如下：