Monte carlo 求解积分

文章目录

• Monte carlo 求解积分
• • @[toc]
  • • 1 单变量情形
    • 2 多变量情形

1 单变量情形

假设待求解积分形式为
$$\theta ={\int }_0^{1}f(x)\mathrm{d}x$$
其中$\theta$为积分值。引入随机变量$X\sim U(0,1)$，则$\mathbf{\theta }=E[f(X)]$。若$X_i(i=1,\dots n)$均服从$U(0,1)$，则$f(X_i)$是均值为$\theta$的独立同分布随机变量。根据大数定律有
$$\sum _{i=1}^k\frac{f\left(X_i\right)}{k}\to E[f(X)]=\theta ,k\to \infty$$
上述公式意味着只需要获得大量服从$U(0,1)$的随机数，通过$f$作用求其均值即可近似于原积分值$\theta$。这种积分近似方法称为Monte carlo(MC)方法。

若积分上下限不为(0,1)，考虑如下积分
$$\theta ={\int }_a^{b}f(x)\mathrm{d}x$$
可以通过如下线性变换进行转化
$$y=\frac{x-a}{b-a},\mathrm{d}y=\frac{\mathrm{d}x}{b-a}$$
于是
$$\theta ={\int }_0^{1}f(a+(b-a)y)(b-a)\mathrm{d}y$$
根据上述思想，可以通过如下步骤实现积分

1 首先构建服从(0,1)均与分布的采集器，并获得$n$各随机数$x_i\in (0,1)$

2 再将所有随机数带入函数$f(a+(b-a)y)(b-a)$求出$n$个函数值

3 对2中$n$个函数值进行平均

下面通过$R$进行MC求解积分
$${\int }_{-2}^2{e}^{-x^2}dx$$

f1 = function(n,lower,upper,fun){
  "
  n：随机数个数
  lower:积分下限
  upper:积分上限
  fun:被积函数
  "
  x = runif(n)
  sum((upper-lower)*fun(lower+(upper-lower)*x))/n
}

# 定义函数
g = function(x) exp(-x^2)
res = numeric()
for(i in 1:10000) res[i] = f1(i,-1,1,g) 
plot(res,type = 'l',xlab = 'n')
# 添加理论值
abline(h = integrate(g,-1,1)$value,col = 'red',lwd = 2)
grid(nx = 20,ny=20,lwd =2)

上图看出，随着模拟次数增加，使用MC方法得到的值与理论值更加接近。其中理论值使用R内嵌函数计算

integrate(g,-1,1)
# 1.493648 with absolute error < 1.7e-14

---

2 多变量情形

对于单变量而言，MC方法作用并不是非常明显，对于多元积分求解具有更高效的作用。

假设多元函数$f$是关于变量$x_i(i=1,2\dots n)$的函数，需要求解
$$\theta ={\int }_0^1{\int }_0^1\cdots {\int }_0^{1}f\left(x_1,x_2,\cdots ,x_n\right)\mathrm{d}{x}_1\mathrm{d}{x}_2\cdots \mathrm{d}{x}_n$$
注意到使用MC方法关键是估计$\theta$
$$\theta =E\left[f\left(X_1,X_2,\cdots ,X_n\right)\right]$$
其中$X_i$为$iid$ 且服从 $U(0,1)$。产生$k$个独立集合，每个集合由$n$个独立的服从$U(0,1)$随机变量构成，
$$\begin{array}{c}{U}_1^1,U_2^1,\cdots ,U_n^1\\ U_1^2,U_2^2,\cdots ,U_n^2\\ ⋮\\ U_1^k,U_2^k,\cdots ,U_n^k\end{array}$$
$g\left(U_1^i,U_2^i,\cdots ,U_n^i\right),i=1,2,\cdots ,k$具有均值$\theta$的独立同分布随机变量，于是当$k\to \infty$
$$\frac{{\sum }_{i=1}^{k}f\left(U_1^i,U_2{}^i,\cdots ,U_n^i\right)}{k}\to E\left[f\left(X_1,X_2,\cdots ,X_n\right)\right]=\theta$$

# 二重积分
X = runif(10000)
Y = runif(10000)
f = function(x,y) cos(x^2+y^2)
sum(f(X,Y))/10000

res2 = numeric()
for(i in 1:2000){
  res2[i] = sum(f(X,Y)[1:i])/i
}
# 理论值
l2 = function(x){
  cos(x[1]^2+x[2]^2)
}
library(cubature)
z = adaptIntegrate(l2, c(0, 0), c(1, 1), maxEval=10000)
# 模拟值
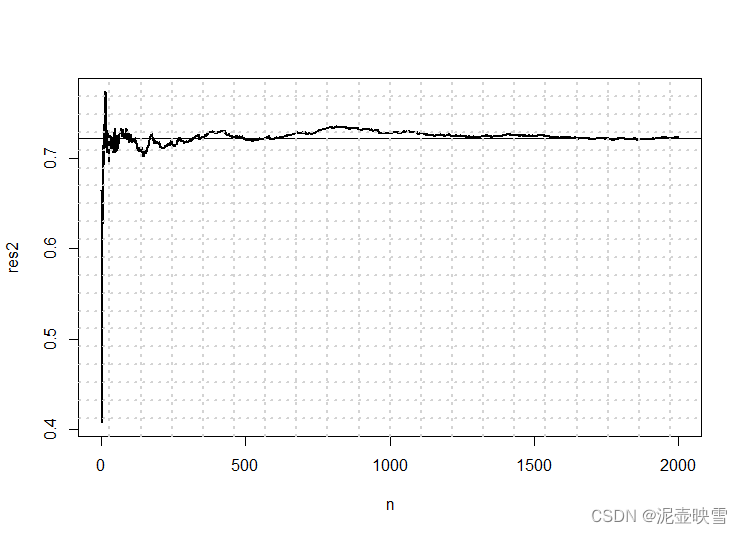
plot(res2,type = 'l',xlab = 'n',lwd = 2)
abline(h = z$integral)
grid(nx = 20,ny=20,lwd =2)

---

-END-