电力系统负荷与电价预测优化模型（Matlab代码实现）

news2024/10/7 7:31:12

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、数据、文章

💥1 概述

用于模拟电价的模型是一个简化形式的混合模型，如下图1所示。其根本驱动因素是天然气价格和气温。该模型在内部捕获了驱动因素与电价的关系之间的关系，以及与一天中的时间、一周中的哪一天和节假日的关系。天然气价格模型是一种简化的均值回归随机微分方程模型。温度模型是参数函数和时间序列模型的组合。
模拟的天然气和电价路径被送入调度算法，该算法计算工厂的最优调度，以产生一系列现金流，可用于计算风险现金流。

图1

详细讲解见第4部分。

📚2 运行结果

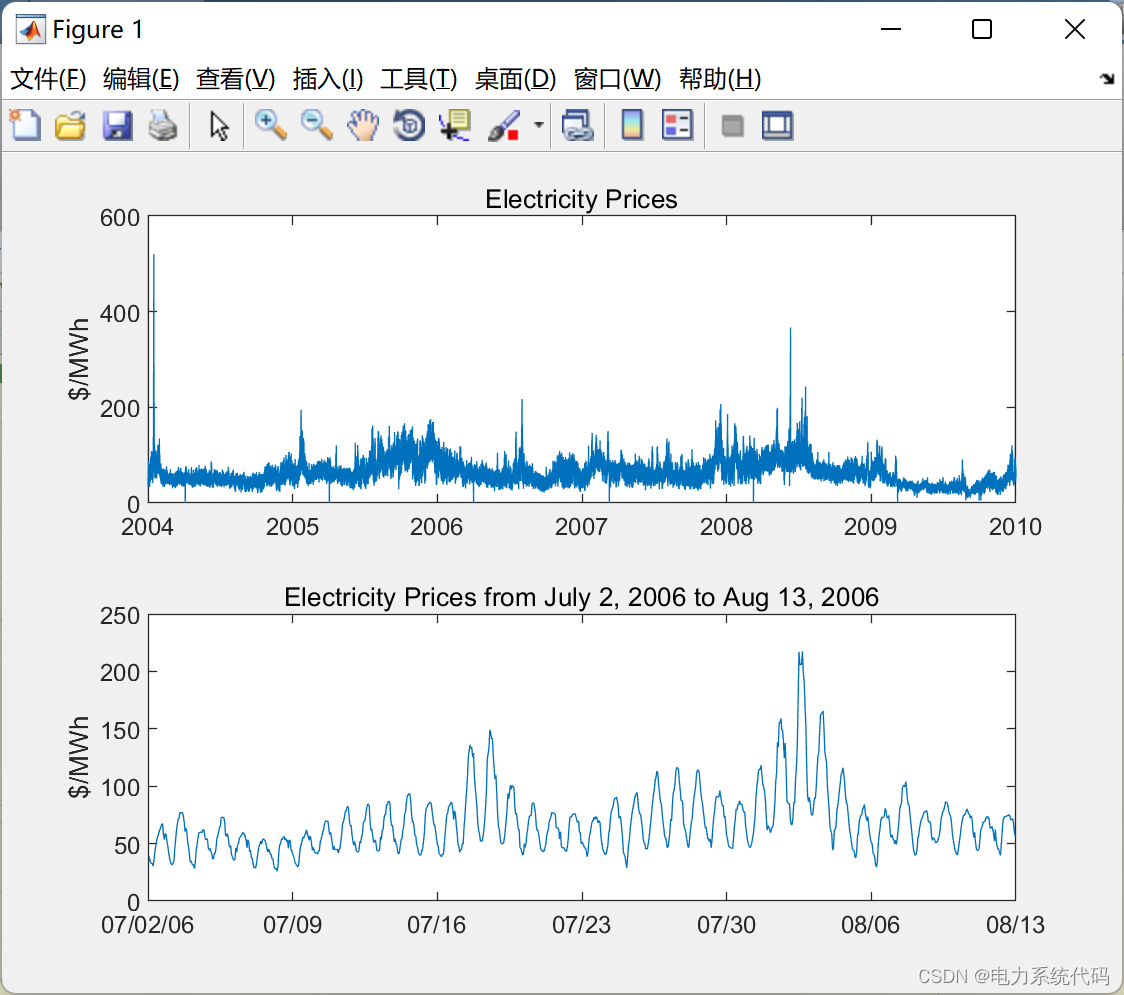
部分代码：

%% 每小时温度建模和模拟
% 这个例子演示了每小时干球温度拟合一个非线性温度模型。
% 温度序列被建模为两个分量的总和，一个确定性的非线性函数，
% 用来解释给定年份某一时刻的季节或预期温度，另一个随机分量，用来解释实际温度与平均值的偏差。
%% 导入数据
%数据集从先前创建的MAT-file中加载。它由一系列日期的向量和相应的历史记录温度组成。
clear
load Data\TempSeries
whos

%% 季节性成分（确定性）
% 确定性或期望的温度分量用正弦和模型建模，激励的是数据中观察到的温度和周期性的物理本质。
% 利用曲线拟合工具箱对模型参数进行估计。统计工具箱函数NLINFIT也可以用来估计模型参数。
% 计算平均值(年平均值)并将其从系列中剔除
m = mean(drybulb)
drybulb0 = drybulb - m;

% Fit double-sine model
model = fit(dates, drybulb0, 'sin2')

%% 可视化模型精度
% 用自定义图对拟合结果进行可视化分析。图中的两个轴是相连的，这极大地使数据的视觉探索。
% 还要注意，X轴上的日期tick相对于缩放和平移是动态的。
pred = model(dates) + m;
res = drybulb - pred;
fitPlot(dates, [drybulb pred], res);
disp(['平均绝对误差: ' num2str(mean(abs(res))) ' 华氏度']);

%% 分析残差中的序列相关性
% 上述图中明显的特征之一是残差不具有序列相关性。预计这是因为高于平均气温很可能跟随高于平均气温。
% 这种序列相关性可以被明确地度量。这里用AUTOCORR和PARCORR函数来显示序列的自相关和部分自相关。
figure;
subplot(2,1,1);
autocorr(res,50);
title('随机序列的序列相关性');
subplot(2,1,2);
parcorr(res(1:1000),50);

%% 利用季节AR模型对随机成分进行建模
% 可以选择对随机分量建模一个均值回复漂移SDE。
% 但是，由于季节性，我们将使用带有季节性滞后的自回归模型。
% 这里可以使用MATLAB反斜杠算子代替REGRESS函数，但这不会返回置信区间。
lags = [1 2 3 4 23 24 25 47 48 49];
Xres = lagmatrix(res, lags);
[beta, betaci, res2] = regress(res, Xres);
disp('滞后系数和置信区间');
disp([lags' beta betaci])

%% 对回归残差进行序列相关分析
%来自回归的残差现在应该大多是序列不相关的。

figure;
subplot(2,1,1);
plot(dates, res2); datetick
title('回归残差及其序列相关性');
subplot(2,1,2);
autocorr(res2(lags(end)+1:end),50);

%% 对残差拟合一个分布
% 由于残差大多是不相关的，因此可以将它们建模为独立的从适当的分布中提取的。
% 一个t位置尺度分布可以显示出很好的拟合性。
PD = fitdist(res2, 'tlocationscale');

%% 模型总结
% 温度模型现在可以定义为，
%
% *平均气温' m '
% *正弦模型'模型'
% *回归参数'β '
% *自相关滞后'滞后'
% *剩馀概率分布PD
% *可选样本前数据( 回归温度的最后一次观测值 )

tempModel = struct('m', m, 'sinmodel', model, 'reglags', lags, 'regbeta', beta, 'dist', PD, 'presample', res(end-lags(end)+1:end));
save SavedModels\TemperatureModel.mat -struct tempModel
clearvars -except tempModel dates drybulb

%% 仿真模型
% 我们现在可以对这个模型进行2009年的模拟，并将模拟值与2009年的观测数据进行比较。
% 注意我们已经捕获了我们模型中的相关特征。
newDates = dates(end-365*24+1:end);
simTemp = simulateTemperature(tempModel, newDates, 1);

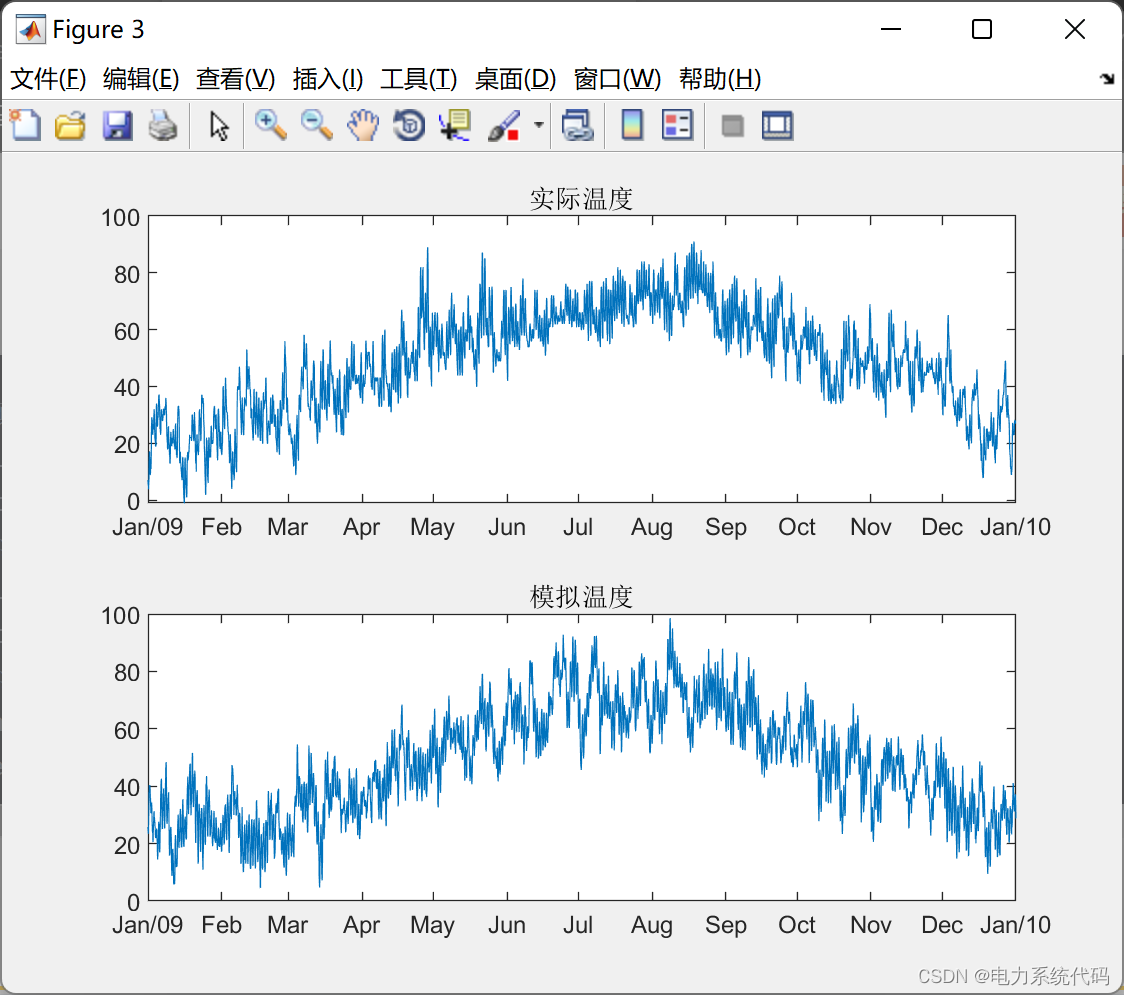
%% 可视化仿真结果
ax1 = subplot(2,1,1);
plot(newDates, drybulb(end-365*24+1:end))
title('实际温度');
ax2 = subplot(2,1,2);
plot(newDates, simTemp);
title('模拟温度');
linkaxes([ax1 ax2], 'x');
dynamicDateTicks([ax1 ax2], 'linked');