🌈欢迎来到C++专栏~~优先级队列的使用 & 模拟实现
- (꒪ꇴ꒪(꒪ꇴ꒪ )🐣,我是Scort
- 目前状态:大三非科班啃C++中
- 🌍博客主页:张小姐的猫~江湖背景
- 快上车🚘,握好方向盘跟我有一起打天下嘞!
- 送给自己的一句鸡汤🤔:
- 🔥真正的大师永远怀着一颗学徒的心
- 作者水平很有限,如果发现错误,可在评论区指正,感谢🙏
- 🎉🎉欢迎持续关注!

list的使用
- 🌈欢迎来到C++专栏~~优先级队列的使用 & 模拟实现
- 一. 优先级队列的使用
- 一. priority_queue的模拟实现
- 🌈size & empty & top
- 🌈仿函数
- 🧐优缺点:
- 🎨push 和向上调整算法
- 🎨pop 和向下调整算法
- 构造函数
- 如果T是自定义类型
- 📢写在最后

优先级队列也是一种 容器适配器,默认情况下它适配的是vector,以支持 堆的算法中频繁的随机访问。下面详细讲解
一. 优先级队列的使用
头文件:<queue>

- Container :默认情况下,它适配的是
vector(因为要大量用到[]找下标)。理论上底层的容器可以是任何标准容器类模板,也可以是其他特定设计的容器类,但是必须支持随机访问迭代器访问,以及一系列基本接口。 - Compare:默认情况下,大的优先级高(即默认是大堆),仿函数给的是
less(这确实有点奇怪)。小堆需要传入仿函数类型,它的头文件在<functional>中
void test_priority_queue()
{
//默认大的优先级高
priority_queue<int> pq;
pq.push(3);
pq.push(1);
pq.push(2);
pq.push(5);
pq.push(9);
pq.push(0);
while (!pq.empty())
{
cout << pq.top() << " ";
pq.pop();
}
cout << endl;
int a[] = { 3, 1, 5, 7, 4, 0, 3, 2 };
priority_queue<int> heap(a, a + sizeof(a) / sizeof(int));//区间初始化
while (!heap.empty())
{
cout << heap.top() << " ";
heap.pop();
}
cout << endl;
}

多说无益,做一道题目上手:215. 数组中的第K个最大元素
方法一:建大堆(堆排) + pop (k-1)次取堆顶
时间复杂度:O(N+k*logN)
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
//建堆 O(N)
priority_queue<int> maxHeap(nums.begin(), nums.end());
//O(logN* K)
while(--k)
{
maxHeap.pop();
}
return maxHeap.top();
}
};
一. priority_queue的模拟实现
priority_queue框架,他的底层是一个随机容器,模板第三个参数(仿函数)后面详谈——
🌈size & empty & top
const T& top()
{
return _con[0];
}
bool empty() const
{
return _con.empty();
}
size_t size() const
{
return _con.size();
}
🌈仿函数
灵活控制的开关(仿函数):是排大堆还是小堆,总不可能改代码吧
我们写一个类,没有任何成员变量,重载了operator()运算符 ——
//仿函数/函数对象 ---- 类 重载了operator()
//类对象可以像函数一样去使用
namespace ljj
{
template<class T>
class less
{
public:
bool operator()(const T& l, const T& r) const
{
return l < r;
}
};
template<class T>
class greater
{
public:
bool operator()(const T& l, const T& r) const
{
return l > r;
}
};
}
priority_queue<int> heap(a, a + sizeof(a) / sizeof(int));
priority_queue<int, vector<int>, greater<int>> heap(a, a + sizeof(a) / sizeof(int));
不同仿函数类型的对象,用()来调用对应的函数比较方式,就实现了像函数一样调用 ——
int main()
{
ljj::less<int> lsFunc;
cout << lsFunc(1, 2) << endl;
//等价于下面
//cout << lsFunc.operator()(1, 2) << endl;
ljj::greater<int> gtFunc;
cout << gtFunc(1, 2) << endl;
return 0;
}
🧐优缺点:
🌍优点如下:
-
在同一时间里,由某个仿函数所代表的单一函数,可能有不同的状态(可以根据不同的类型代表不同的状态)
-
仿函数即使定义相同,也可能有不同的类型(可以有不同类型)
-
仿函数使程序代码变简单(仿函数在一定程度上使代码更通用,本质上简化了代码)
🌍缺点:
- 仿函数通常比一般函数速度慢
🎨push 和向上调整算法
优先级队列的插入及删除,就是在堆的基础上做插入删除,学到这我还回去复习了一下堆
堆插 = 尾插+ 向上调整
//插入 —— 向上调整
void push(const T& x)
{
_con.push_back(x);
adjust_up(_con.size()-1);
}
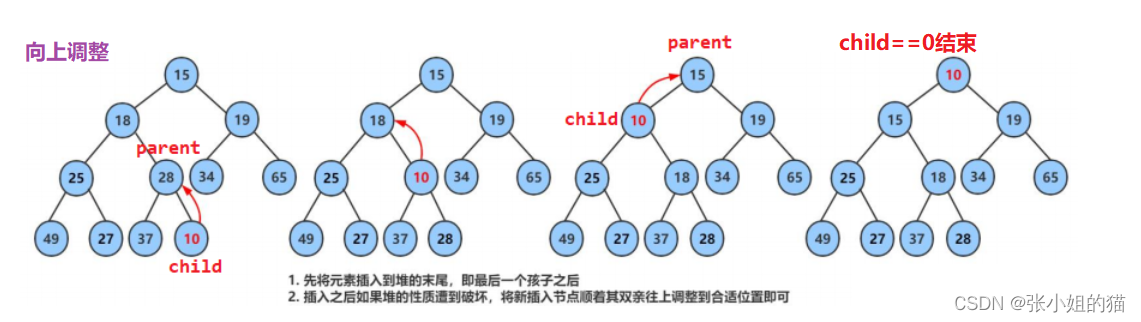
🍅重头戏:向上调整算法 (看图5分钟内写出来,才可以)
//向上调整
void adjust_up(size_t child)
{
Compare com;//仿函数
int parent = (child - 1) / 2;
while (child > 0)
{
//if ( _con[child] > _con[parent])
if (com(_con[parent] , _con[child]))
{
std::swap(_con[child], _con[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
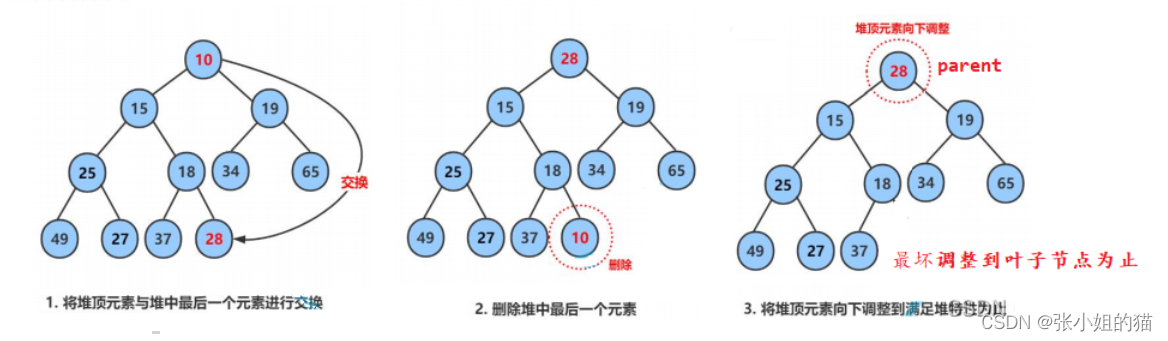
🎨pop 和向下调整算法
堆删 = 交换 + 删除 + 向下调整(不会破坏树的结构)
//交换 —— 删除 —— 向下调整
void pop()
{
std::swap(_con[0], _con[_con.size() - 1]);
_con.pop_back();
adjust_down(0);
}
💦向下调整算法
//高度次 logN
void adjust_down(size_t parent)
{
Compare com;//仿函数
size_t child = parent * 2 + 1;//左孩子
while (child < _con.size())
{
//左右孩子选大的交换
//if (child + 1 < size() && _con[child + 1] > _con[child])
if (child + 1 < size() && com(_con[child], _con[child + 1]))
{
++child;
}
//if (_con[child] > _con[parent])
if (com(_con[parent], _con[child]))
{
std::swap(_con[child], _con[parent]);
parent = child;
child = parent + 1;
}
else
{
break;
}
}
}
建大堆还是建小堆本质是由于ajust_up和ajust_down中的比较符号不同,那么就要通过仿函数来控制

构造函数
🌈 迭代器区间构造:_con自定义类型会调用它的迭代器区间构造,不用再迭代器遍历+push了。在这基础上还要构建成堆,为了使左右都是大(小)堆且向下调整是O(N),要倒着建,从最后一个非叶子节点(即最后一个节点的父亲)开始向下调整。
priority_queue()
{}
//迭代器区间构造
template<class InputIterator>
priority_queue(InputIterator first, InputIterator last)
{
while (first != last)
{
_con.push_back(*first);
++first;
}
//向下调整 建堆
for (int i = (_con.size() - 1 - 1) / 2; i >= 0; --i)
{
adjust_down(i);
}
}
如果T是自定义类型
⚡我们考虑到如果T 是日期类Date等 —— 要看情况
- 如果是类里面有支持比较大小的,就直接用 比如:
string类 - 如果是库里面的、人家写好的类,我们只能写仿函数,我们不可能改人家的代码,如果是自己写的类,二者都可以(看情况)
- 但有些情况是必须写仿函数的,因为原生比较大小的行为不一定是我们想要的,比如:Date*比较大小,但是我们不想用指针比较,那就写仿函数
void test_priority_queue()
{
//priority_queue<Date> pq;
priority_queue<Date, vector<Date>, greater<Date>> pq;
pq.push(Date(2022, 3, 26));
pq.push(Date(2022, 4, 1));
pq.push(Date(2022, 2, 19));
pq.push(Date(2022, 4, 10));
while (!pq.empty())
{
cout << pq.top() << endl;
pq.pop();
}
}
我们当然可以重载这些运算符
但是如果数据类型 不支持比较 或 比较的方式不是你想要的,可以自己实现仿函数,按照你想要的方式(Compare给我们留的口子)去控制比较逻辑,比如 —— 我想比较地址大小:Date*
void test_priority_queue3()
{
//priority_queue<Date*> pq; //默认比较地址大小
//priority_queue<Date*, vector<Date*>, lessPDate> pq;
priority_queue<Date*, vector<Date*>, greaterPDate> pq;
pq.push(new Date(2022, 3, 26));
pq.push(new Date(2022, 4, 1));
pq.push(new Date(2022, 2, 19));
pq.push(new Date(2022, 4, 10));
//默认比较地址大小,若想比较日期大小,自己写仿函数
while (!pq.empty())
{
cout << *pq.top() << endl;
pq.pop();
}
}
于是我们自己写了仿函数,又因为私有成员类外无法访问,我们把这两个仿函数类声明为priority_queue的友元类 ——
struct lessPDate
{
bool operator()(const Date* d1,const Date* d2)
{
//return *d1 < *d2;
return (d1->_year < d2->_year) ||
(d1->_year == d2->_year && d1->_month < d2->_month) ||
(d1->_year == d2->_year && d1->_month == d2->_month && d1->_day < d2->_day);
}
};
struct greaterPDate
{
bool operator()(const Date* d1, const Date* d2)
{
//return *d1 > *d2;
return (d1->_year > d2->_year) ||
(d1->_year == d2->_year && d1->_month > d2->_month) ||
(d1->_year == d2->_year && d1->_month == d2->_month && d1->_day > d2->_day);
}
};
📢写在最后
好奇,我偷偷溜出去,都能被辅导员发现,表情如下