时间序列预测（二）基于LSTM的销售额预测

小O：小H，Prophet只根据时间趋势去预测，会不会不太准啊

小H：你这了解的还挺全面，确实，销售额虽然很大程度依赖于时间趋势，但也会和其他因素有关。如果忽略这些因素可能造成预测结果不够准确

小O：那有没有什么办法把这些因素也加进去呢？

小H：那尝试下LSTM吧～

LSTM是一个循环神经网络，能够学习长期依赖。简单的解释就是它在每次循环时，不是从空白开始，而是记住了历史有用的学习信息。理论我是不擅长的，有想深入了解的可在网上找相关资料学习，这里只是介绍如何利用LSTM预测销售额，在训练时既考虑时间趋势又考虑其他因素。

本文主要参考自使用 LSTM 对销售额预测，但是该博客中的介绍数据与上期数据一致，但实战数据又做了更换。为了更好的对比，这里的实战数据也采用上期数据。

数据探索

import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import seaborn as sns
from fbprophet import Prophet
from sklearn.metrics import mean_squared_error
from math import sqrt
import datetime
from xgboost import XGBRegressor
from sklearn.metrics import explained_variance_score, mean_absolute_error, \
mean_squared_error, r2_score  # 批量导入指标算法

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM
from tensorflow.keras.layers import Dense, Dropout
from sklearn.preprocessing import MinMaxScaler
from keras.wrappers.scikit_learn import KerasRegressor
from sklearn.model_selection import GridSearchCV

以下数据如果有需要的同学可关注公众号HsuHeinrich，回复【数据挖掘-时间序列01】自动获取～

# 读取数据
raw_data = pd.read_csv('train.csv')
raw_data.set_index('datetime', inplace=True)
raw_data.head()

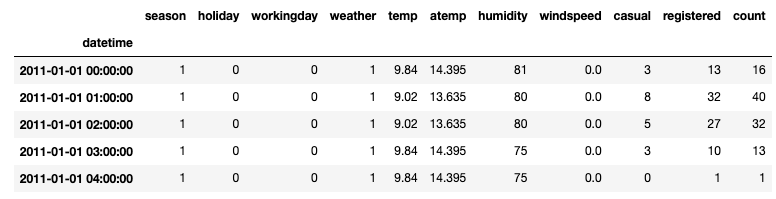
特征工程

# 拆分数据集
num = 24*14 # 将最后2周划分为测试集
train, test = raw_data.iloc[:-num,:], raw_data.iloc[-num:,:]

# 数据缩放
scaler = MinMaxScaler(feature_range=(0,1))
train_scaled=scaler.fit_transform(train)
test_scaled=scaler.transform(test)

# 构造XY(样本数+时间步数+特征数)
def createXY(dataset, n_past, target_p=-1):
    '''
    将数据集构造成LSTM需要的格式
    dataset：数据集
    n_past：时间步数，利用过去n的时间作为特征,以下一个时间的目标值作为当前的y
    target_p：目标值在数据集的位置，默认为-1
    '''
    dataX = []
    dataY = []
    for i in range(n_past, len(dataset)):
        dataX.append(dataset[i - n_past:i, 0:dataset.shape[1]])
        dataY.append(dataset[i,target_p])
    return np.array(dataX),np.array(dataY)

X_train, Y_train=createXY(train_scaled,30)
X_test, Y_test=createXY(test_scaled,30)
X_train.shape

(10520, 30, 11)

可以看到有10520个训练样本，每个样本的形状为30*11，即过去30天的数据集合（30个样本，11个特征）。Y实际为30个样本下一个样本的y值。即第0个训练样本X为原始数据df中[0-29]的所有数据，第0个训练Y为原始数据df中第30个样本的y值

# 定义LSTM
def build_model(optimizer):
    grid_model = Sequential()
    grid_model.add(LSTM(4, return_sequences=True, input_shape=(X_train.shape[1], X_train.shape[2])))
    grid_model.add(LSTM(4)) # 防止预测值为三维
    grid_model.add(Dropout(0.2))
    grid_model.add(Dense(1))
    grid_model.compile(loss = 'mse',optimizer = optimizer)
    return grid_model 

grid_model=KerasRegressor(build_fn=build_model,verbose=1,validation_data=(X_test,Y_test))
 
parameters = {'batch_size' : [16,20],
            'epochs' : [8,10],
            'optimizer' : ['adam','Adadelta'] }
 
grid_search = GridSearchCV(estimator = grid_model,
                            param_grid = parameters,
                            cv = 2)

<ipython-input-41-930ab96e3919>:11: DeprecationWarning: KerasRegressor is deprecated, use Sci-Keras (https://github.com/adriangb/scikeras) instead. See https://www.adriangb.com/scikeras/stable/migration.html for help migrating.
  grid_model=KerasRegressor(build_fn=build_model,verbose=1,validation_data=(X_test,Y_test))

模型拟合

模型输出

# 模型拟合
grid_search = grid_search.fit(X_train,Y_train)
grid_search.best_params_

# 输出最优模型参数
print(grid_search.best_params_)
# 获取最优模型
model_lstm=grid_search.best_estimator_.model
# 预测值
pre_y=model_lstm.predict(X_test)

{'batch_size': 16, 'epochs': 8, 'optimizer': 'adam'}

模型评估

# 逆缩放
# 构造同等宽度的pre_y，即生成与缩放同等列数
pre_y_repeat = np.repeat(pre_y, X_train.shape[2], axis=-1)
# 逆缩放并获取预测值
pred=scaler.inverse_transform(np.reshape(pre_y_repeat,(len(pre_y), X_train.shape[2])))[:,-1] # 选取目标列所在位置

# 对Y_test进行逆缩放
Y_test_repeat = np.repeat(Y_test, X_train.shape[2], axis=-1)
Y_test_original=scaler.inverse_transform(np.reshape(Y_test_repeat,(len(Y_test),X_train.shape[2])))[:,-1] # 选取目标列所在位置

# 评估指标
model_metrics_functions = [explained_variance_score, mean_absolute_error, mean_squared_error,r2_score]  # 回归评估指标对象集
model_metrics_list = [[m(Y_test_original, pred) for m in model_metrics_functions]]  # 回归评估指标列表
regresstion_score = pd.DataFrame(model_metrics_list, index=['model_xgbr'],
                   columns=['explained_variance', 'mae', 'mse', 'r2'])  # 建立回归指标的数据框
regresstion_score  # 模型回归指标

	explained_variance	mae	mse	r2
model_xgbr	0.764219	58.990179	7276.310243	0.749074

结果展示

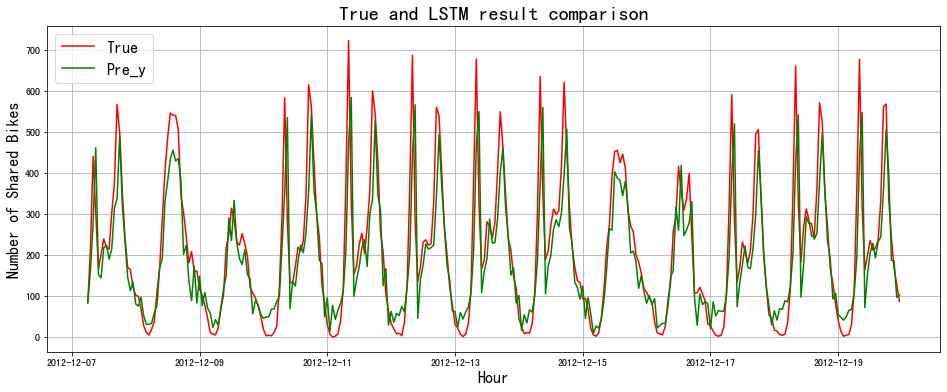
预测结果可视化

# 模型效果可视化
fig = plt.figure(figsize=(16,6))
plt.title('True and LSTM result comparison', fontsize=20)
# 时间索引
ds_index = [datetime.datetime.strptime(x, "%Y-%m-%d %H:%M:%S") for x in test.index[30:]]
# 真实序列
true_s=pd.Series(Y_test_original, index=ds_index)
plt.plot(true_s, color='red')
# 预测序列
pre_s=pd.Series(pred, index=ds_index)
plt.plot(pre_s, color='green')
plt.xlabel('Hour', fontsize=16)
plt.ylabel('Number of Shared Bikes', fontsize=16)
plt.legend(labels=['True', 'Pre_y'], fontsize=16)
plt.grid()
plt.show()

预测未来值

# 预测未来值
# 历史30日数据作为构造第一条数据
df_30_days_past=raw_data.iloc[-30:,:]
# 读取未来数据
start_time = '2012-12-19 23:00:00' # 原始数据最后一条记录
end_time=[]
for i in range(30):
    
    time_temp = (datetime.datetime.strptime(start_time, "%Y-%m-%d %H:%M:%S") + datetime.timedelta(
        hours=i+1)).strftime("%Y-%m-%d %H:%M:%S")
    end_time.append(time_temp)

future=pd.read_csv("test.csv",parse_dates=["datetime"],index_col=[0])
df_30_days_future=future.loc[end_time,:]

# 补充缺失的列
df_30_days_future["registered"]=0
df_30_days_future["casual"]=0 # 测试样本缺失
df_30_days_future["count"]=0 # 测试样本缺失

# 构造旧新样本
old_scaled_array=scaler.transform(df_30_days_past)
new_scaled_array=scaler.transform(df_30_days_future)
new_scaled_df=pd.DataFrame(new_scaled_array)
new_scaled_df.iloc[:,-1]=np.nan # 对目标列的0修改为nan
full_df=pd.concat([pd.DataFrame(old_scaled_array),new_scaled_df]).reset_index().drop(["index"],axis=1)

full_df_scaled_array=full_df.values
all_data=[]
time_step=30
for i in range(time_step,len(full_df_scaled_array)):
    data_x=[]
    data_x.append(
        full_df_scaled_array[i-time_step :i , 0:full_df_scaled_array.shape[1]])
    data_x=np.array(data_x)
    prediction=model_lstm.predict(data_x)
    all_data.append(prediction)
    full_df.iloc[i,-1]=prediction # 替换目标列的nan

new_array=np.array(all_data)
new_array=new_array.reshape(-1,1)
prediction_copies_array = np.repeat(new_array,data_x.shape[2], axis=-1)
y_pred_future_30_days = scaler.inverse_transform(np.reshape(prediction_copies_array,(len(new_array),data_x.shape[2])))[:,-1]
print(y_pred_future_30_days)

# 因为测试样本casual和registered缺失，故预测不准确

[ 67.19963   28.726665  53.639095  77.41373   84.80948   97.550125
 105.34982  105.89546  105.45314  101.901405  98.7133    96.72031
 101.96429  107.16215  110.38648  111.0147   110.34529  109.8532
 107.00935  102.02435   91.798004  92.968605  93.628006  94.56274
 102.24291  113.515884  87.92808   78.71299   72.63906   70.64108 ]

总结

可以发现，预测效果还不错。如果在做预测的时候，不仅有时间序列数据，还有获得额外的因素，可以尝试使用LSTM进行预测～

共勉～