104、二叉树最大深度

        

        给定一个二叉树，找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

 测试代码：

class TreeNode:
    def __init__(self, val=None, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


class Solution:
    """二叉树层序遍历迭代解法"""

    def levelOrder(self, root):



s = Solution()
# 构造一个二叉树，此处省略了构造函数的实现
# tree = TreeNode()

tree = TreeNode(3)
tree.left=TreeNode(9)
tree.right = TreeNode(20)
tree.right.left = TreeNode(15)
tree.right.right = TreeNode(7)

print(s.levelOrder(tree))  # 输出 [1, 2, 3]

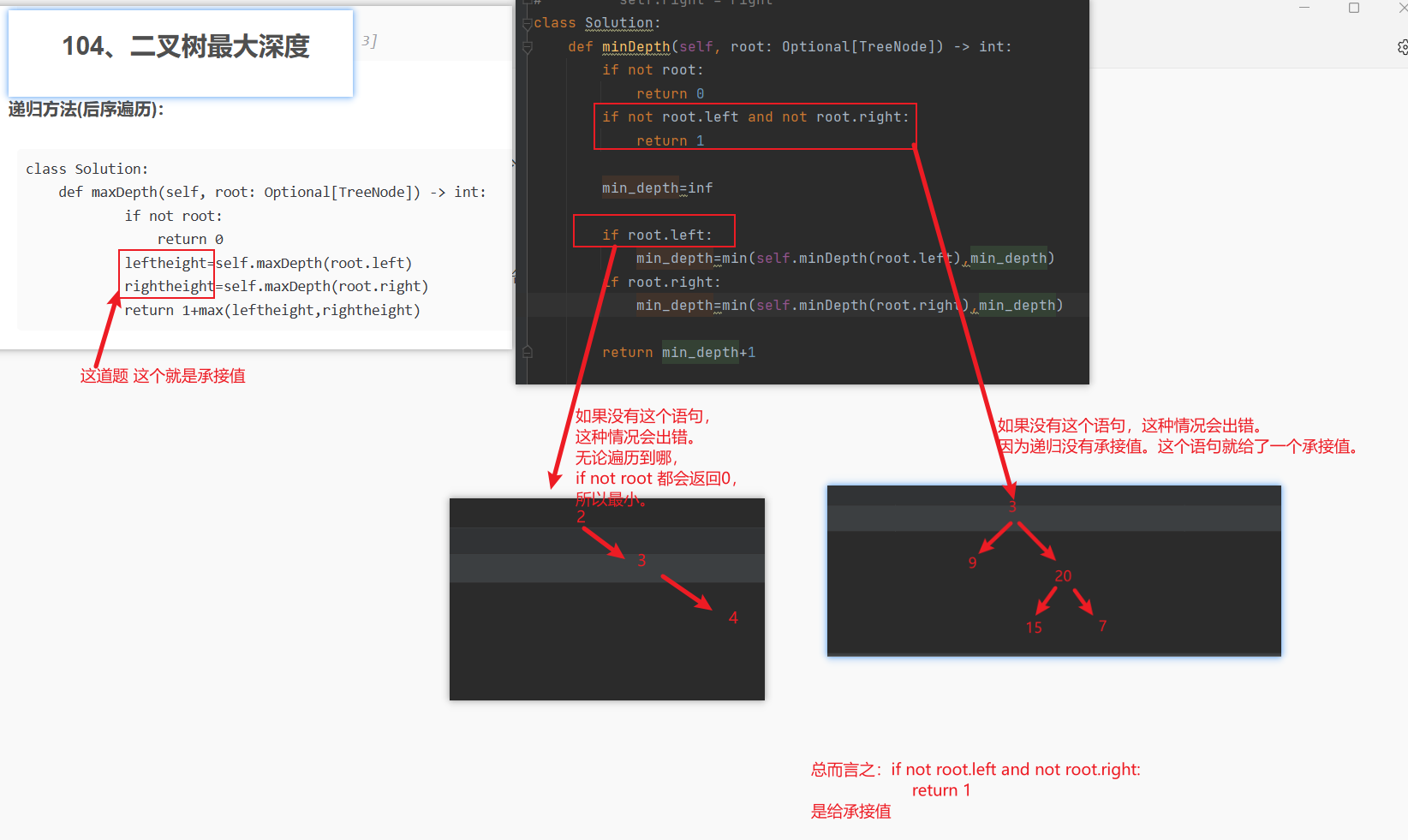
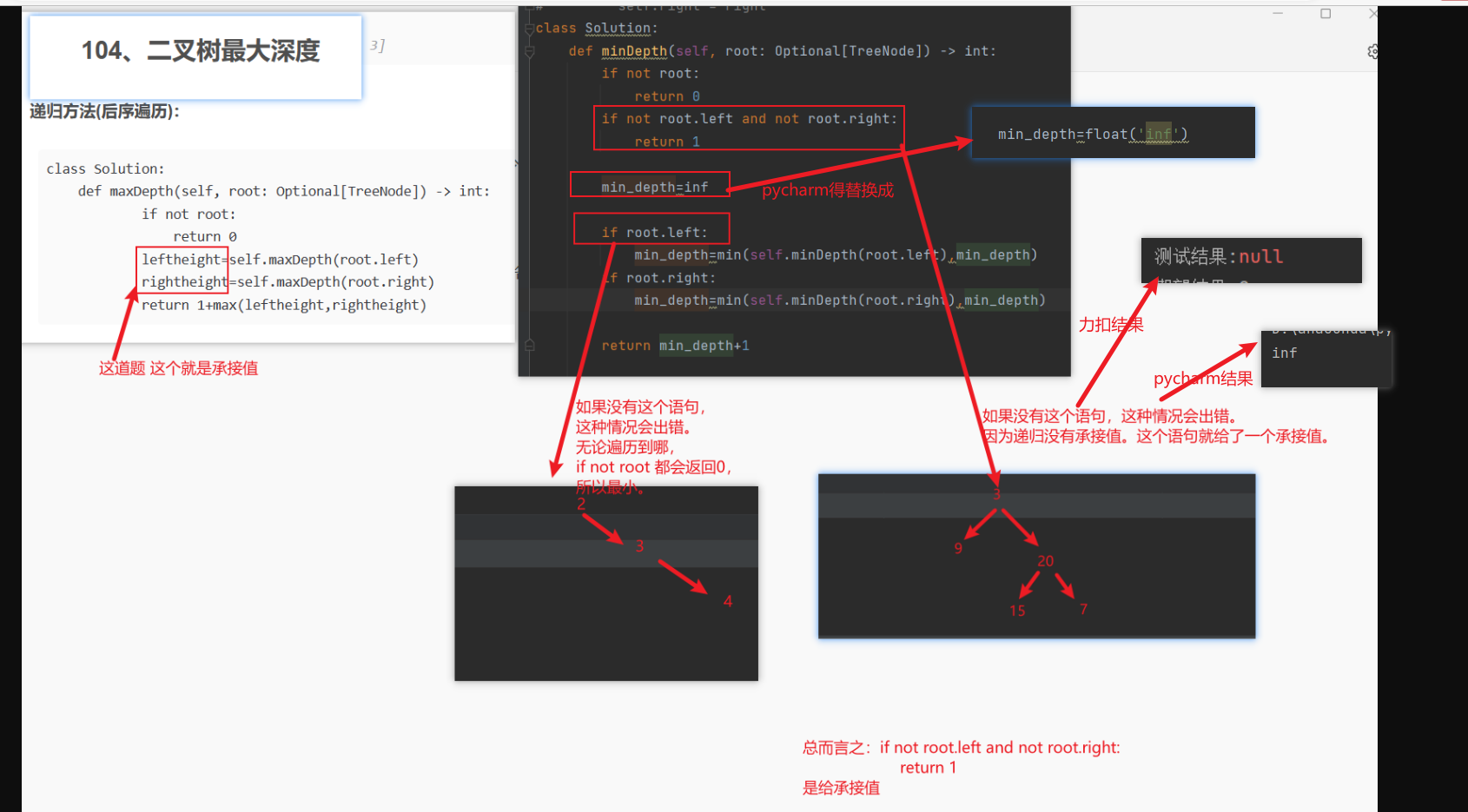
递归方法(后序遍历)：

class Solution:
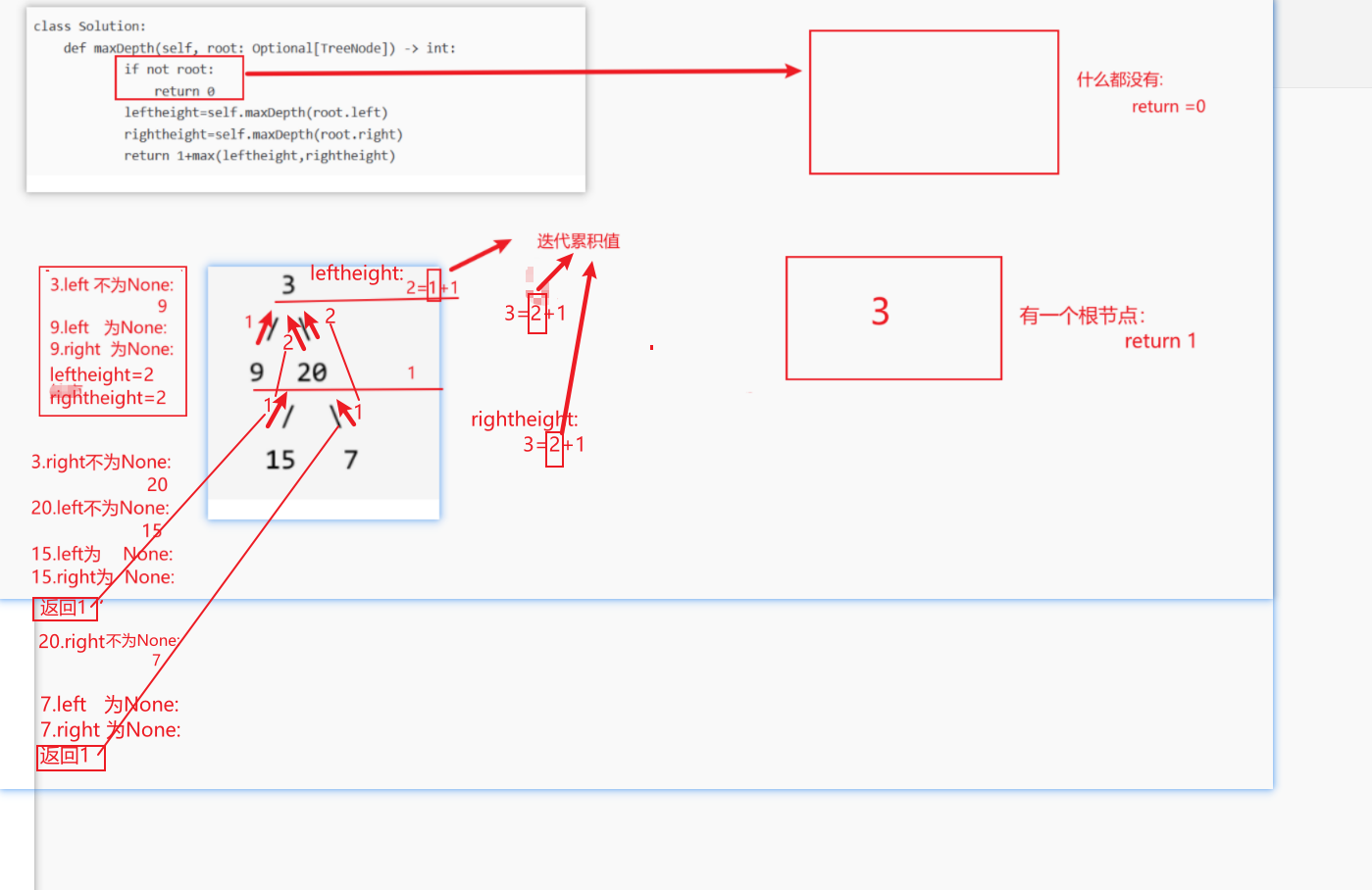
    def maxDepth(self, root: Optional[TreeNode]) -> int:
            if not root:
                return 0
            leftheight=self.maxDepth(root.left)
            rightheight=self.maxDepth(root.right)
            return 1+max(leftheight,rightheight)

        思路详解：

 

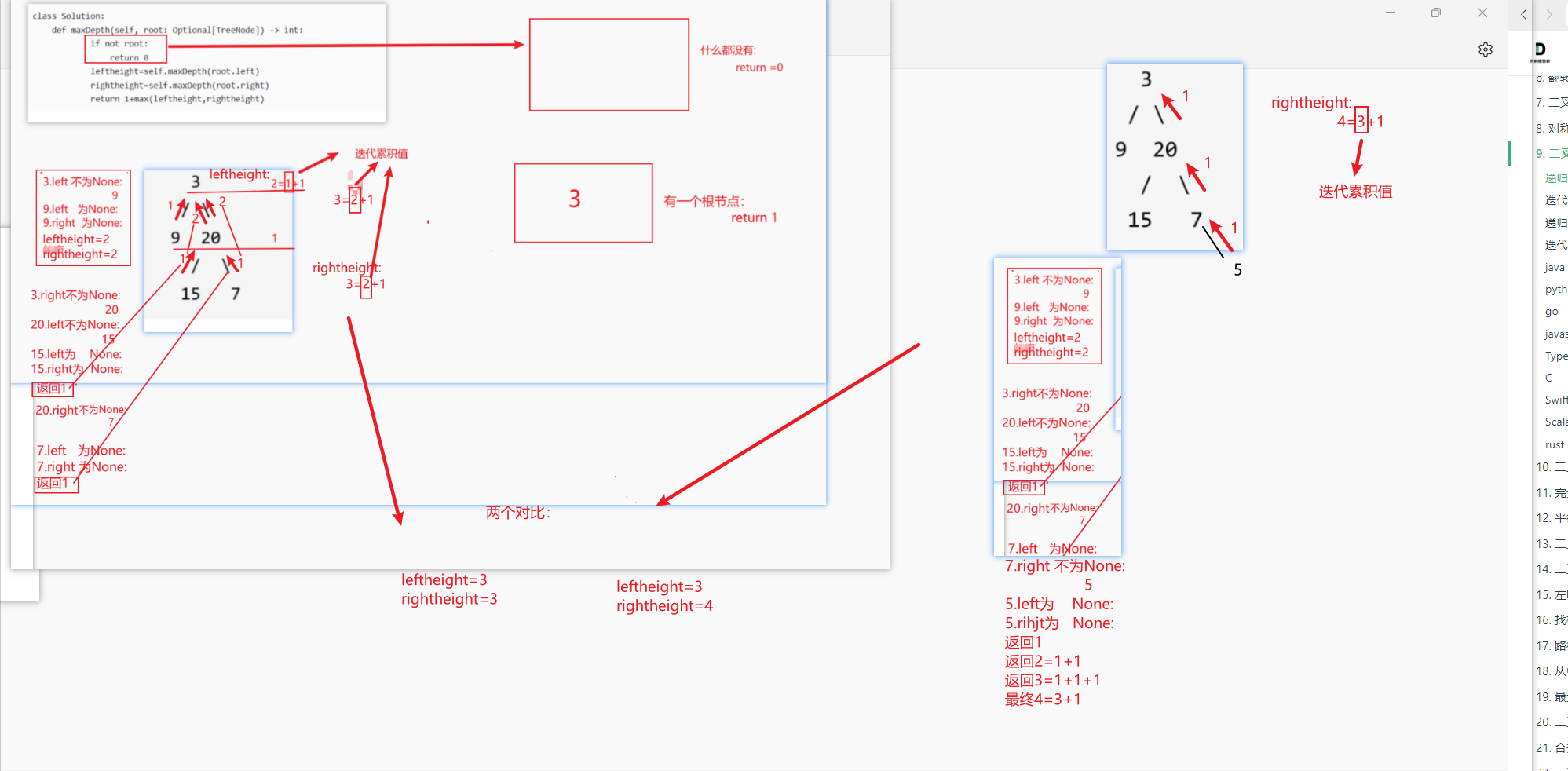
 111.二叉树的最小深度

        给定一个二叉树，找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。说明: 叶子节点是指没有子节点的节点。

        深度优先算法(递归)：

class Solution:
    def minDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        if not root.left and not root.right:
            return 1

        min_depth=inf

        if root.left:
            min_depth=min(self.minDepth(root.left),min_depth)
        if root.right:
            min_depth=min(self.minDepth(root.right),min_depth)

        return min_depth+1

        递归，处理左右子树的各种情况(if-else):

class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root: return 0

        ans = 0
        if not root.left and not root.right: 	# 叶子节点
            ans = 1
        elif root.left and root.right:  # 左右子树均不为空
            ans = min(self.minDepth(root.left), self.minDepth(root.right)) + 1
        elif root.left:		# 左子树不为空 & 右子树为空
            ans = self.minDepth(root.left) + 1
        else:			# 左子树为空 & 右子树不为空
            ans = self.minDepth(root.right) + 1
        return ans

 

 

222.完全二叉树的节点个数

        看懂我上面两道题解析，这道题完全看得懂。

        递归代码：

class Solution:
    def countNodes(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        return self.countNodes(root.right)+self.countNodes(root.left)+1