1.用递归的方法1+2+3+…+N的值(in:5,out:15)
def dg(n):
if n==1:
return 1
else:
return dg(n-1)+n
n=int(input())
print(dg(n))
2.输出斐波那契数列的第N项,0,1,1,2,3,5,8,13…(in:3,out:1)
def feibo(n):
if n==1:
return 0
if n==2 or n==3:
return 1
return feibo(n-1)+feibo(n-2)
n=int(input())
print(feibo(n))
3.求n!(in:5,out:120)n!=123…*n
def fact(n):
if n==0 or n==1:
return 1
return fact(n-1)*n
n=int(input())
print(fact(n))
4.阿克曼(ackmann)函数A(m,n)中,m,n定义域是非负整数(m<=3,n<=10),函数值定义为(m,n in:2 3,out:9):
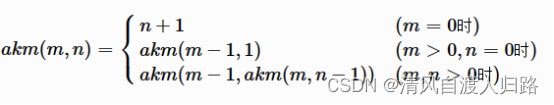
def akm(m,n):
if m==0:
return n+1
elif m>0 and n==0:
return akm(m-1,1)
elif m>0 and n>0:
return akm(m-1,akm(m,n-1))
a=input().split(' ')
print(akm(int(a[0]),int(a[1])))
5.有5个人坐在一起,问第五个人多少岁,他说比第四个人大1岁;问第四个人多少岁,他说比第三个人大一岁;问第三个人多少岁,他说比第二个人大一岁,问第二个人多少岁,他说他比第一个人大一岁,问第一个人多少岁,他说他8岁,请问第5个人多少岁。(in:5,Out:12)
def age(n):
if n==1:
return 8
return age(n-1)+1
n=int(input())
print(age(n))
6.儿童节那天,有6位同学参加了钓鱼比赛,他们每个人钓到的鱼的数量都各不相同。问第一位同学钓了多少条鱼时,他指着第二位同学说比他多钓两条,问第二位同学,他又说比第三位同学多钓了两条鱼。最后问到第6位同学时,他又说自己钓了3条鱼。请问第一位同学钓了多少条鱼?(in:1,out:13)
def fish(n):
if n==6:
return 3
return fish(n+1)+2
n=int(input())
print(fish(n))
7.设一共有n级台阶的楼梯,某人每步可走1级,也可以走2级,用递推的方式可以计算出某人从底层开始走完全部台阶的走法。例如,当n=3时,共有3种走法,即1+1+1,1+2,2+1.当n=6时,从底层开始走完全部台阶的走法共有多少种?(dt)
def stairs(n):
if n==1:
return 1
if n==2:
return 2
return stairs(n-1)+stairs(n-2)
n=int(input())
print(stairs(n))
8.小马需要将N件物品从河的一岸搬运到河的另一岸,每次搬运的物品为1到3件。请问小马将N件物品全部搬运过去有多少种方案
例如: N=3,将3件物品全部搬运过去有4种方案:
方案一: 第一次搬运1件,第一次搬运1件,第三次搬运1件;
方案二: 第一次搬运1件,第二次搬运2件;
方案三: 第一次搬运2件,第二次搬运1件:
方案四: 一次搬运3件。
输入描述
输入一个正整数N,表示需要搬运的物品数输出描述输出将N件物品全部搬运过去有多少种方案
样例输入:3
样例输出:4
样例输入:4
样例输出:7
def river(n):
if n==1:
return 1
if n==2:
return 2
if n==3:
return 4
return river(n-1)+river(n-2)+river(n-3)
print(river(4))
9.设计一个算法,汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。有三个单字符字符串和一个整数。三个字符表示三个杆子的编号,整数为盘子的数目。
根据上述计算规则,补全下列代码。
函数名:hannota(n,a,b,c)
参数表:n – 正整数表示盘子数,a --a杆子,b --b杆子,c --c杆子。
返回值:移动路径。
示例:n=3,返回:
A --> C
A --> B
C --> B
A --> C
B --> A
B --> C
A --> C
sum=0
def hainu(n,a,b,c):
global sum
if n==1:
sum+=1
print(a,"->",c)
else:
hainu(n-1,a,c,b)
hainu(1,a,b,c)
hainu(n-1,b,a,c)
hainu(3,"a","b","c")
print(sum)
10.有一张 m*n 个小方格的地图,一个机器人位于地图的左上角(如图标记为Start 的地方),它每步只能向右或者向下移动一格,如果走到右下角的终点(如图标记为 Finish 的地方),有多少种不同的方法?
例如,一个 3x2 的地图,行走的方法数是 3 种,分别是
1.右>右>下
2.右>下->右
3.下->右>右
输入描述: 两个整数 m(m<=100)和 n(n<=100),代表地图的行数和列数
输出描述: 一个整数,表示行走的方法数。
[样例输入]
88
[样例输出]
3432
m=int(input())
n=int(input())
sum=0
def mm(a,b):
global sum
if a>m:
return
if b>n:
return
if a==m and b==n:
sum+=1
mm(a+1,b)
mm(a,b+1)
mm(1,1)
print(sum)
10.描述
把M个同样的苹果放在N个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?(用K表示)5,1,1和1,5,1 是同一种分法。
输入
第一行是测试数据的数目t(0 <= t <= 20)。以下每行均包含二个整数M和N,以空格分开。1<=M,N<=10。
输出
对输入的每组数据M和N,用一行输出相应的K。
样例输入
1
7 3
样例输出
8
def apple(m,n):#m:苹果数,n:盘子数
if m==0:
return 1
if n==0:
return 0
if n>m:
return apple(m,m)
return apple(m,n-1)+apple(m-n,n)
print(apple(7,3))
11.描述
给出一个正整数a,要求分解成若干个正整数的乘积,即a = a1 * a2 * a3 * … * an,并且1 < a1 <= a2 <= a3 <= … <= an,问这样的分解的种数有多少。注意到a = a也是一种分解。
输入
第1行是测试数据的组数n,后面跟着n行输入。每组测试数据占1行,包括一个正整数a (1 < a < 32768)
输出
n行,每行输出对应一个输入。输出应是一个正整数,指明满足要求的分解的种数
样例输入
2
2
20
样例输出
1
4
def fun(a,b):
if a==1:
return 1
if b==1:
return 0
if a%b==0:
return fun(a//b,b)+fun(a,b-1)
return fun(a,b-1)
n=int(input())
for i in range(n):
m=int(input())
print(fun(m,m))