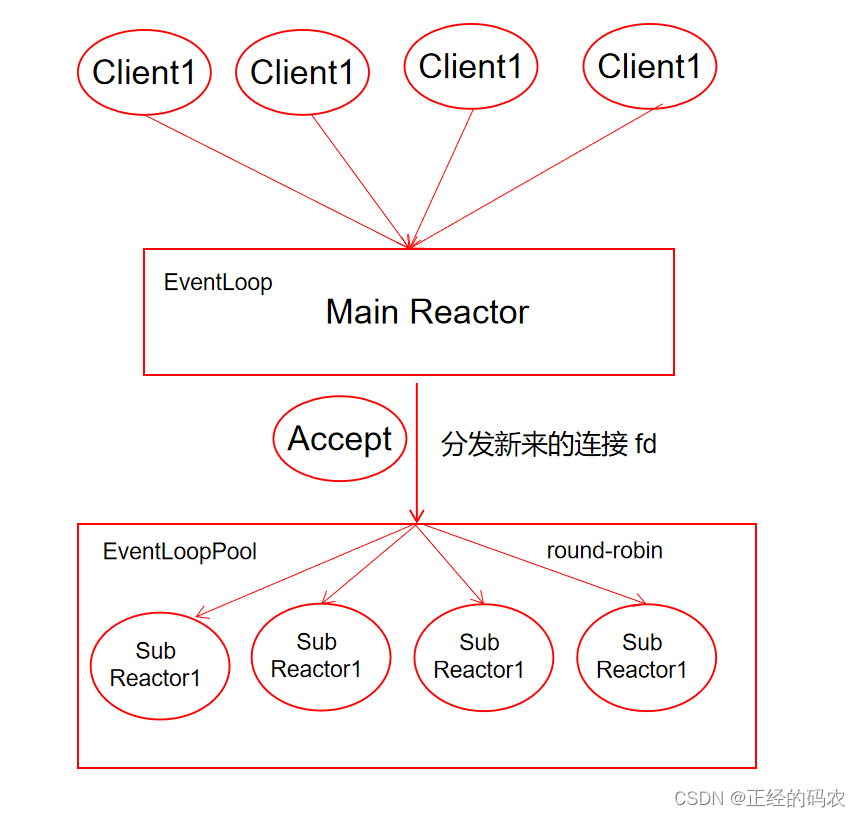
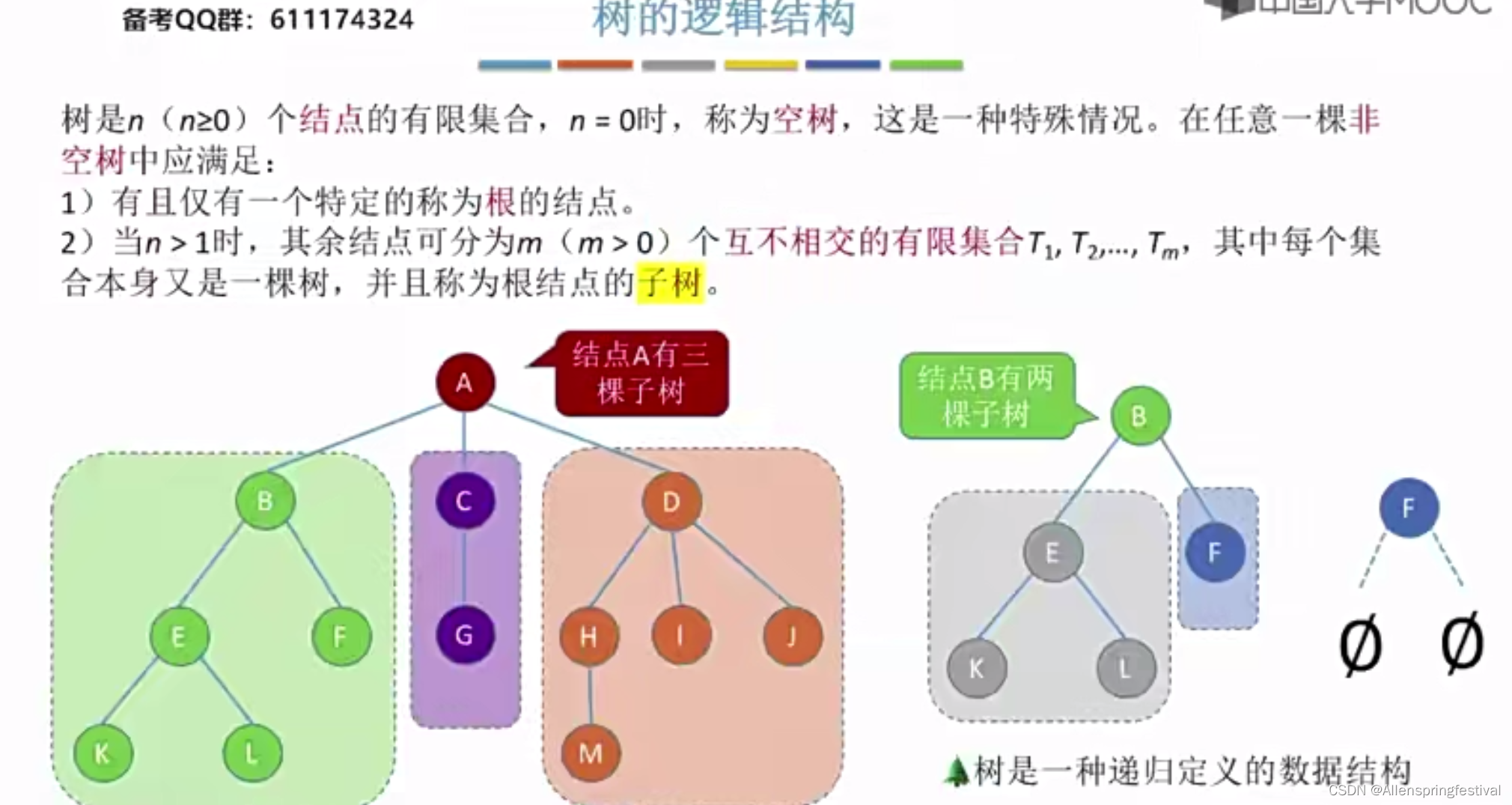
回忆一下树的逻辑结构:
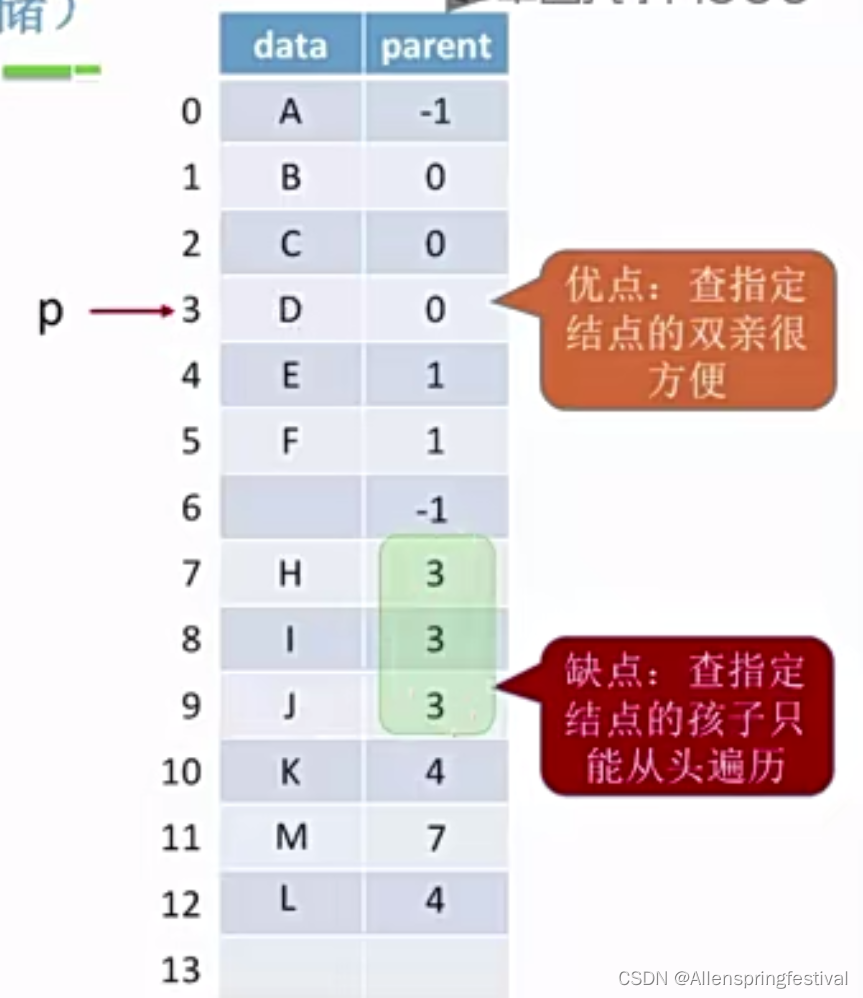
双亲表示法(顺序存储)
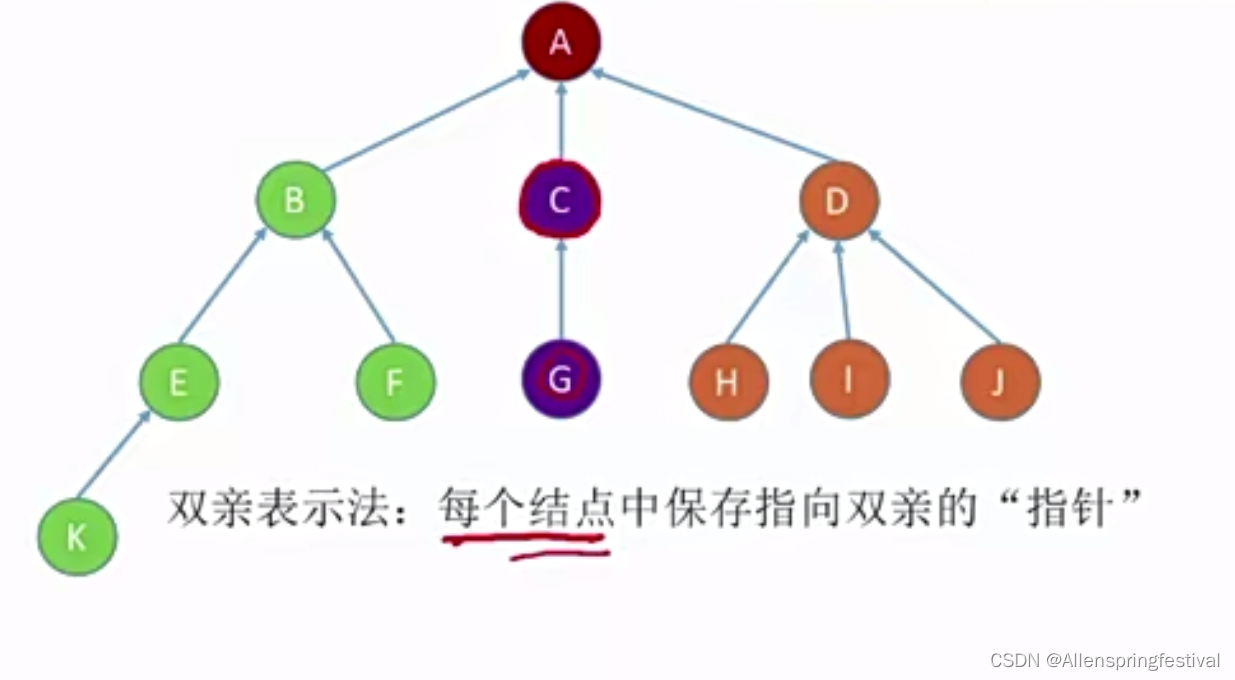



如果增加一个结点M,L。毋须按照逻辑上的次序存储。
如果是删除元素:
方案一:比如说删除元素为G,设置其双亲结点为-1。

方案二:
把尾部的结点提上来。

还需要改变数值让结点数减1。

还要删除以他为根节点的子孙节点。
来回顾一下二叉树的顺序存储:
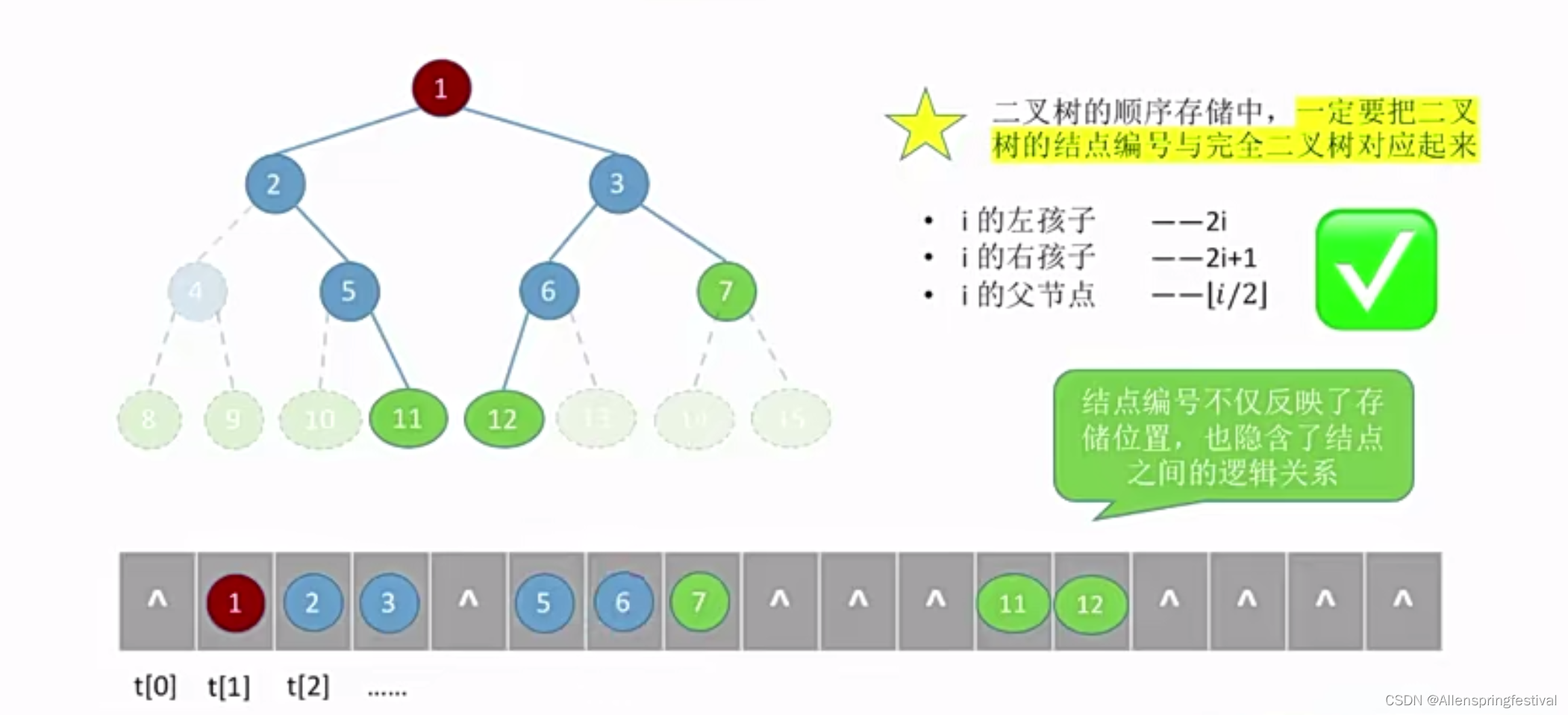
可以根据结点编号不仅反映了存储位置,也隐含了结点之间的逻辑关系。
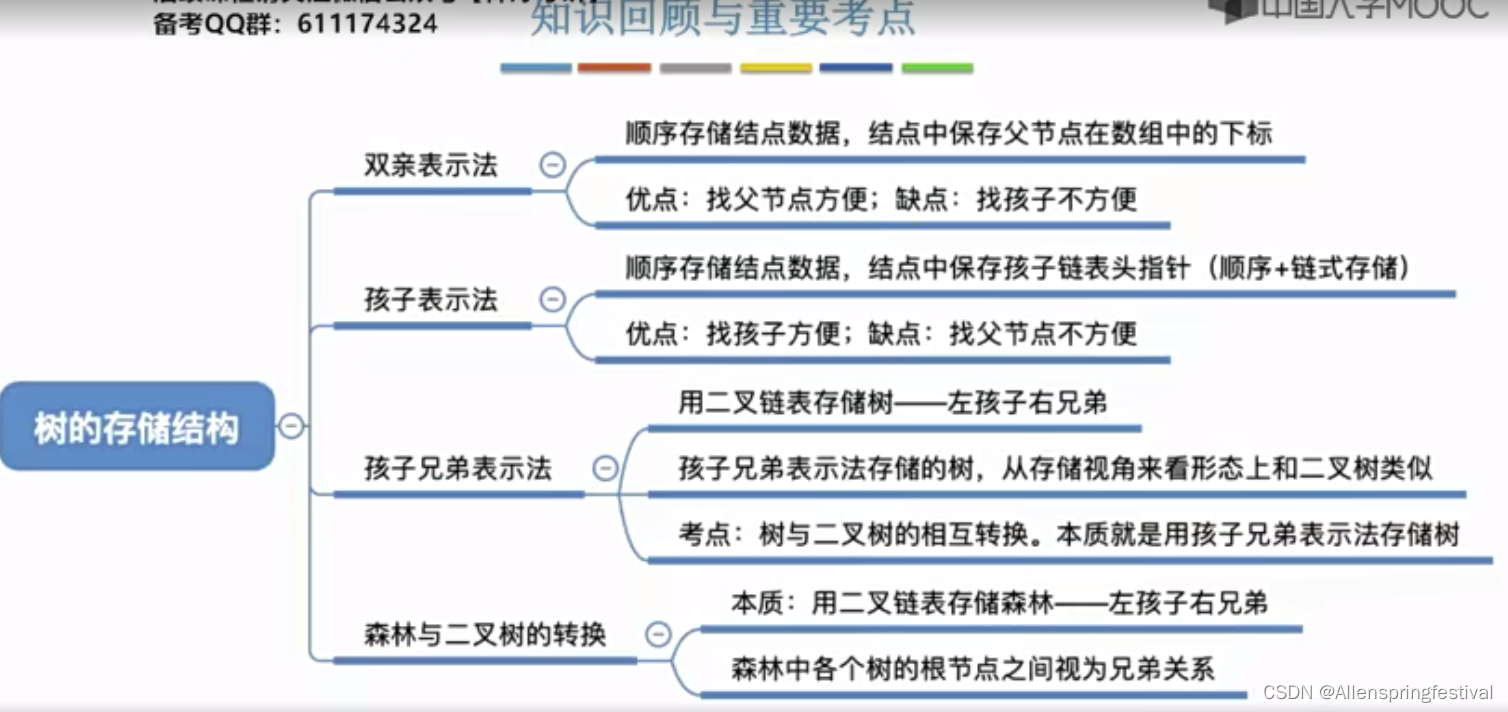
下面来讲解树的孩子表示法
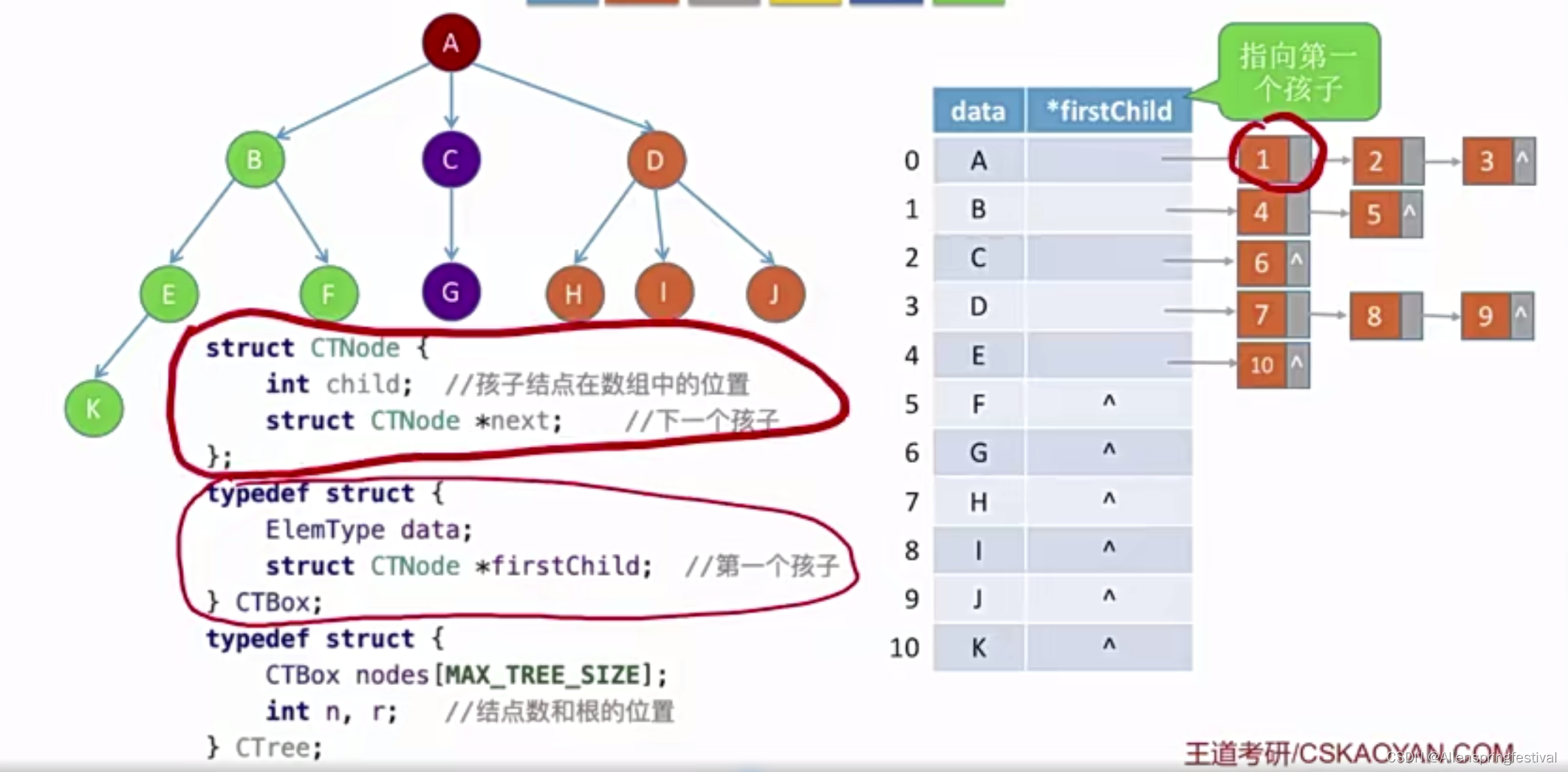

下面就是孩子兄弟表示法(链式存储)
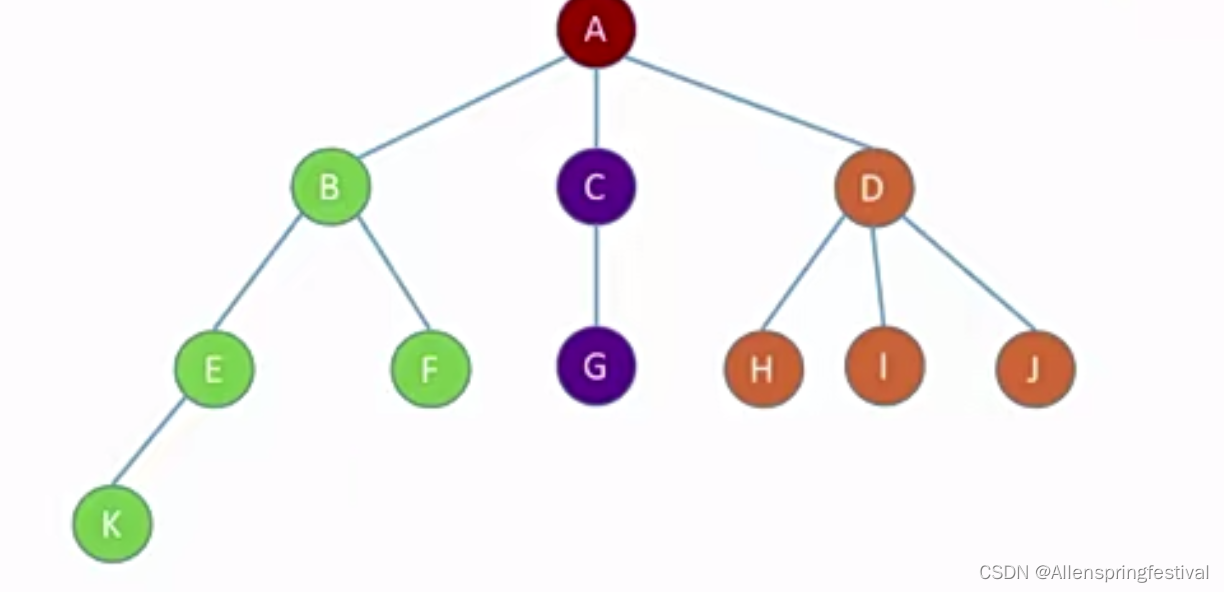

一个数据域,两个指针
其实是跟二叉树的链式存储时一样的

只是名称有所不同

就得到了孩子兄弟法得到了树
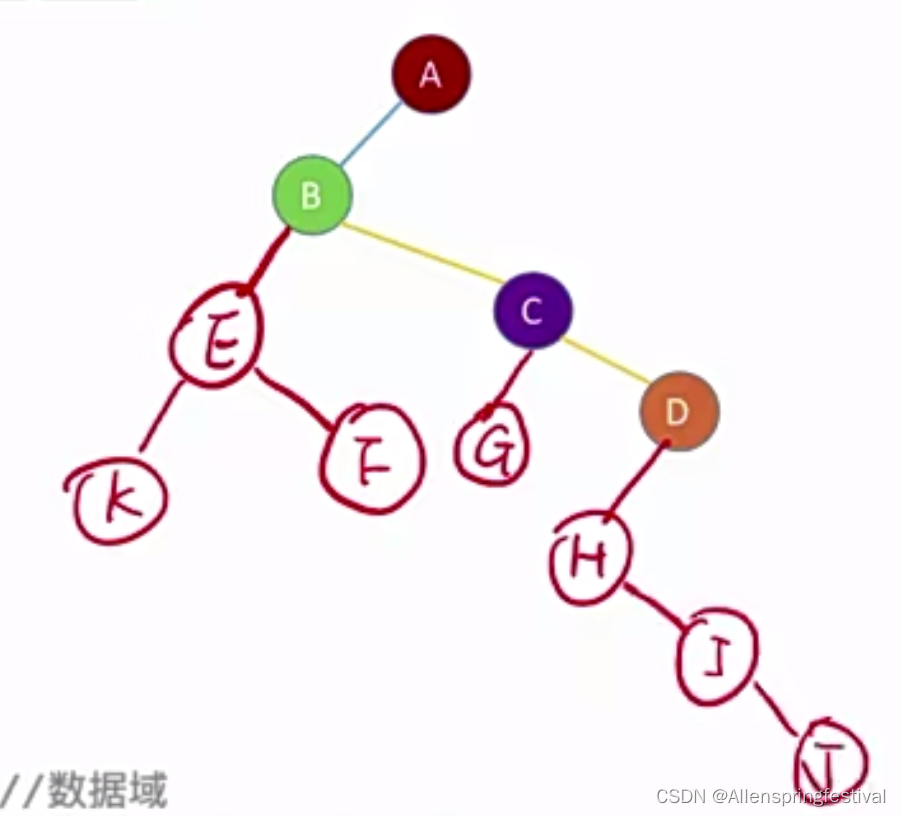
是不是二叉树和树就可以相互转化了。
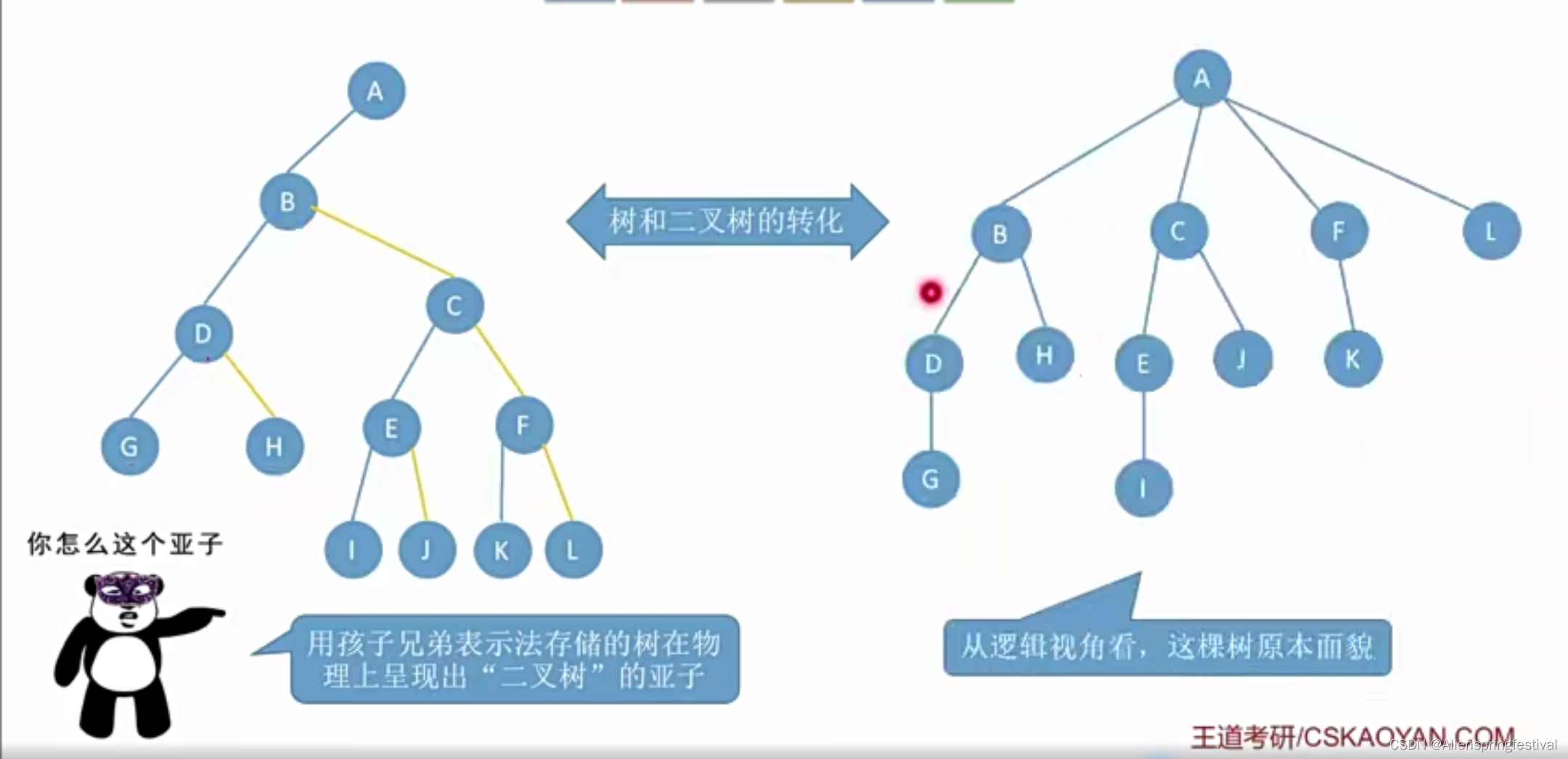
接下来看森林和二叉树的相互转换:
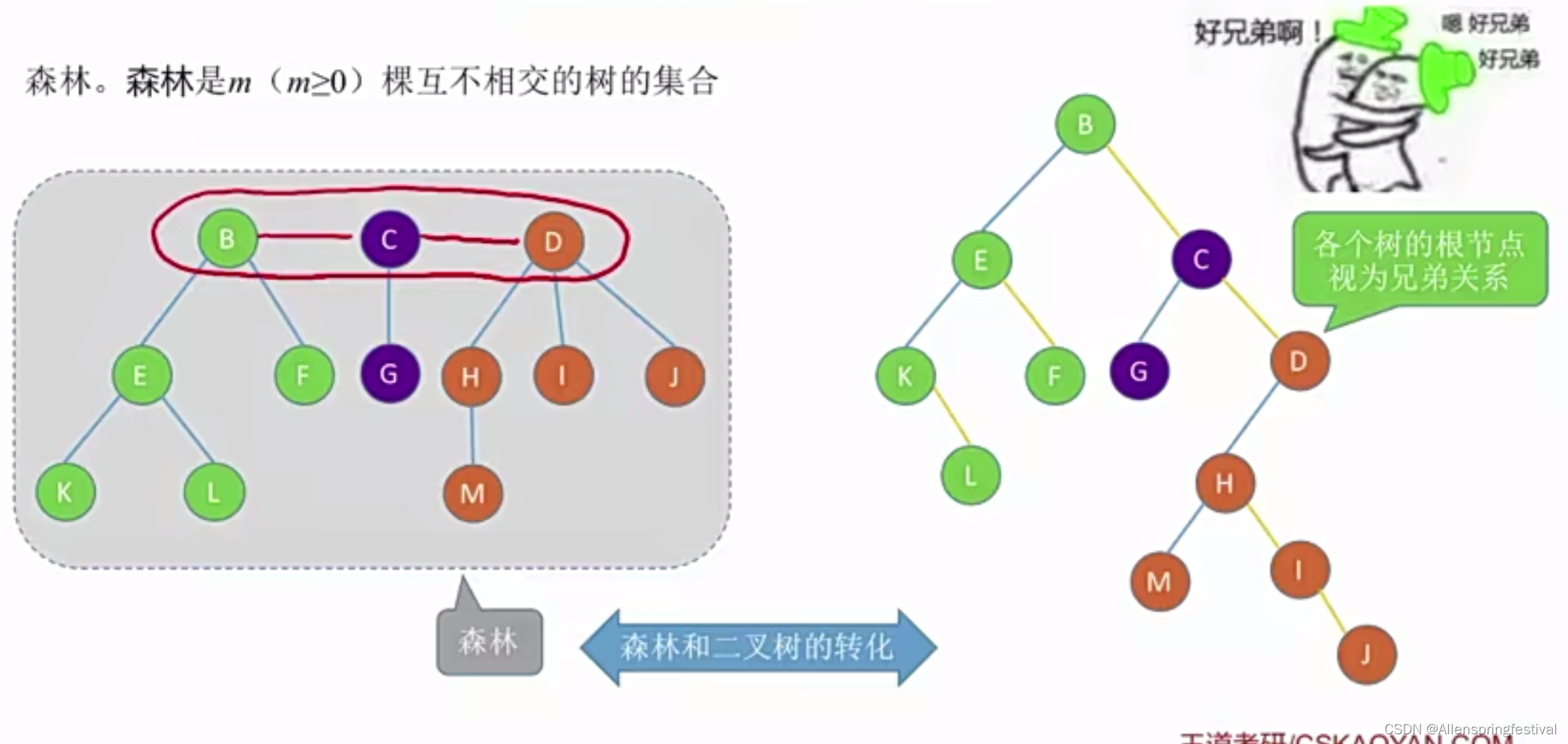
再把二叉树转换为森林:

5.4.2树和森林的遍历
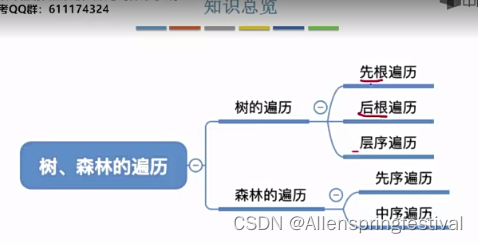
树的遍历
1)树的先根遍历
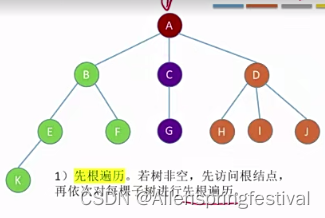
那么对这颗树进行先根遍历的话那么顺序是这样的:
先是ABCD
然后A(BEF)(CG)(DHIJ)
最后A(B(EK)F)(CG)(DHIJ)
伪代码实现:

树和二叉树的转换
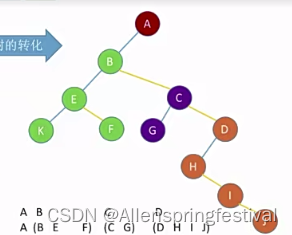
二叉树的先序遍历序列和树的先根遍历序列相同
2)树的后根遍历
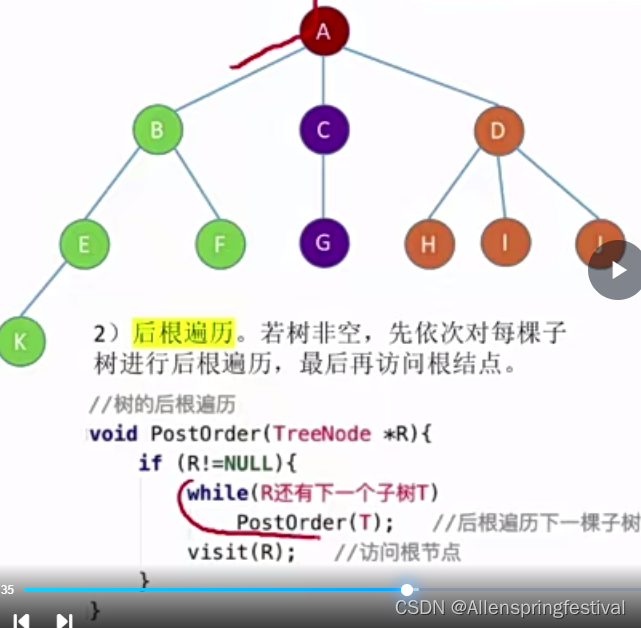
先依次对每棵子树进行后根遍历,最后在访问根节点。
遍历序列如下:


先往下往左走
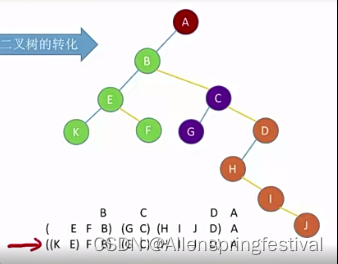
对二叉树的中序遍历序列是相同的。
3)树的层次遍历
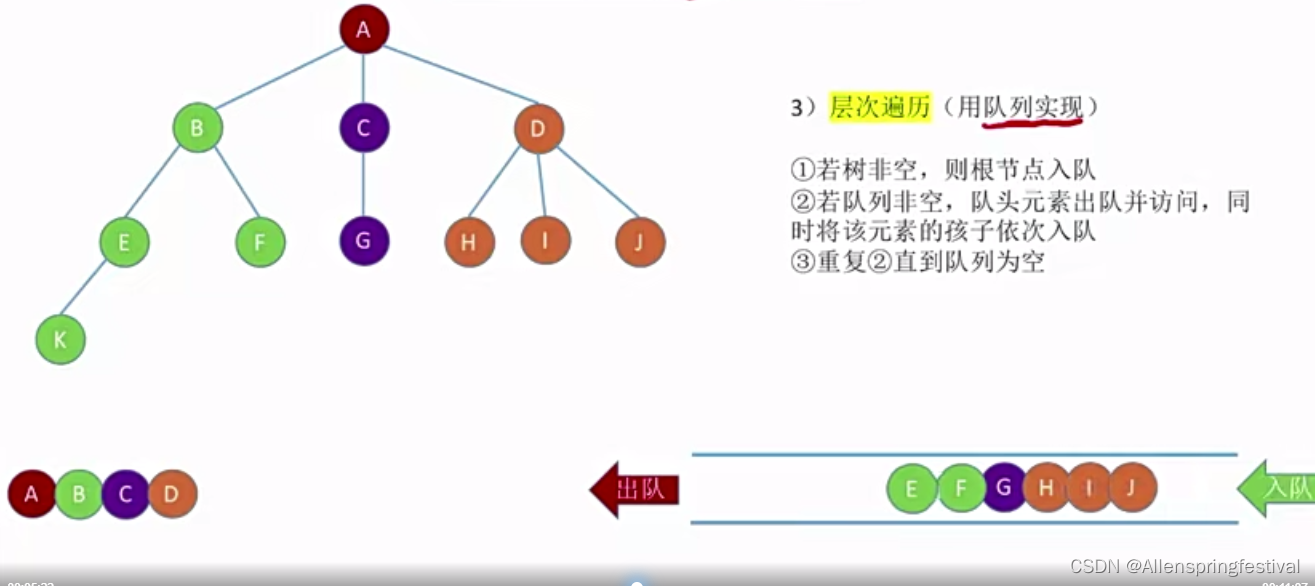
最后在队列中的元素依次出队。
先根遍历和后根遍历需要往深处走,所以我们称之为深度优先遍历。
层序遍历我们称之为广度优先遍历。
下面我们再来看对森林的遍历
1)先序遍历
森林是m(m>=0)棵互不相交的树的集合。每棵树去掉根节点之后,其各个子树又组成森林。
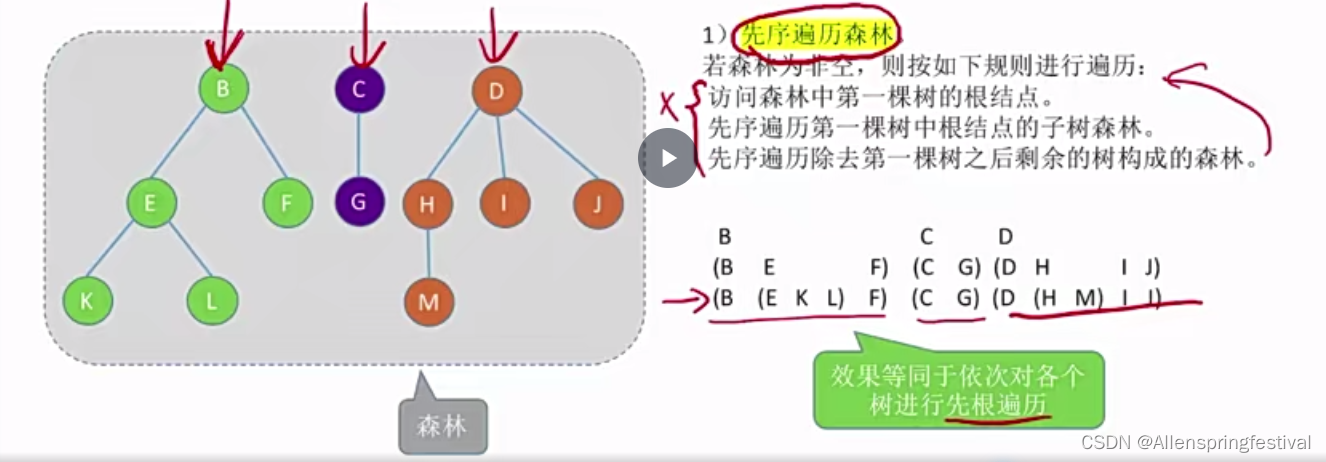
也可以先把森林转换成与之对应的二叉树:
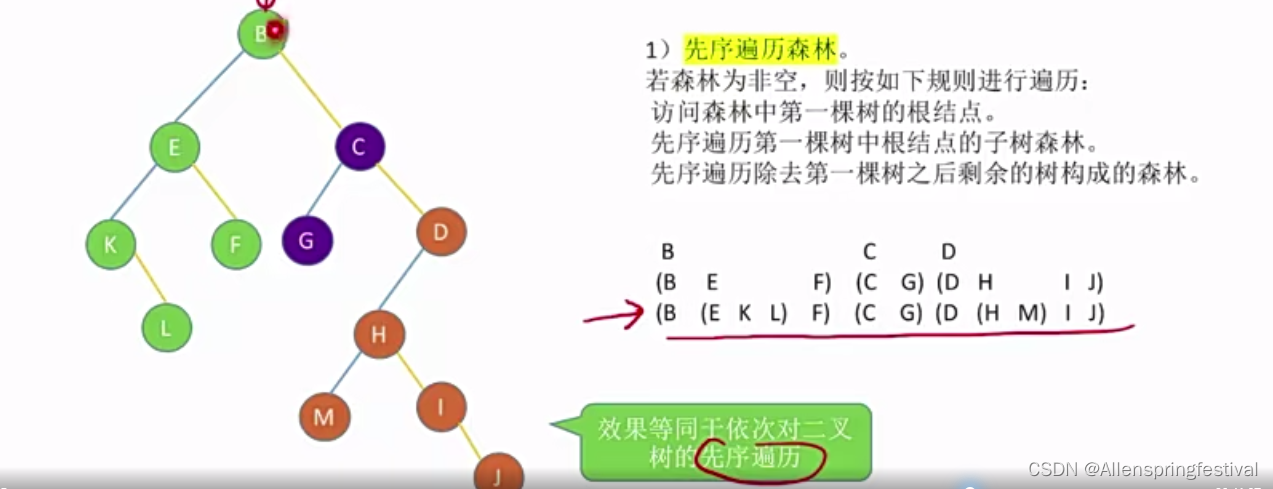
效果等同于依次对二叉树的先序遍历
2)中序遍历
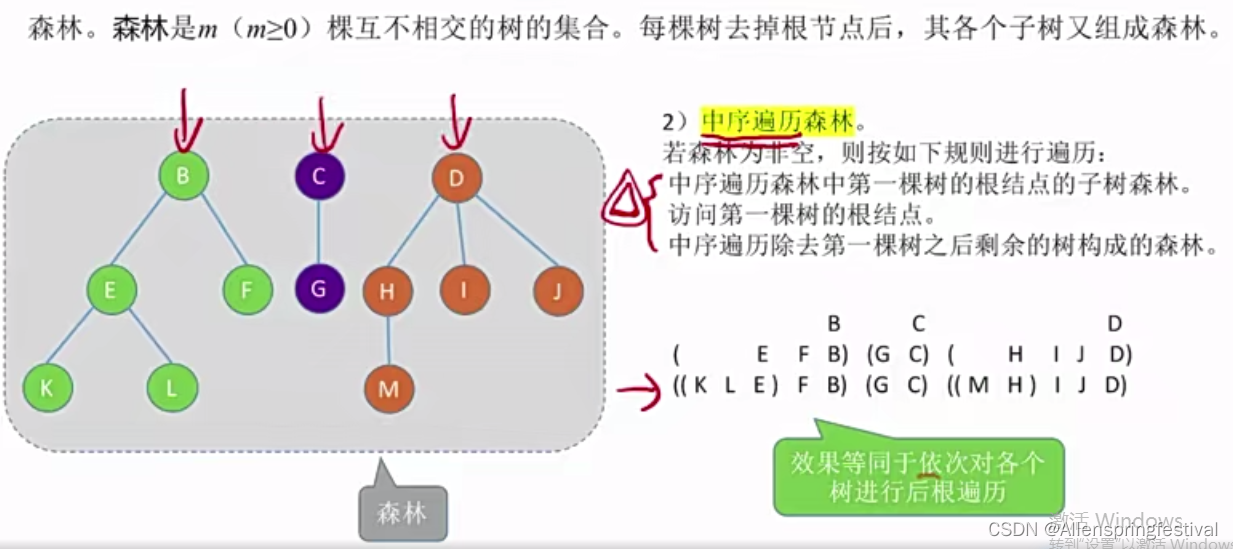
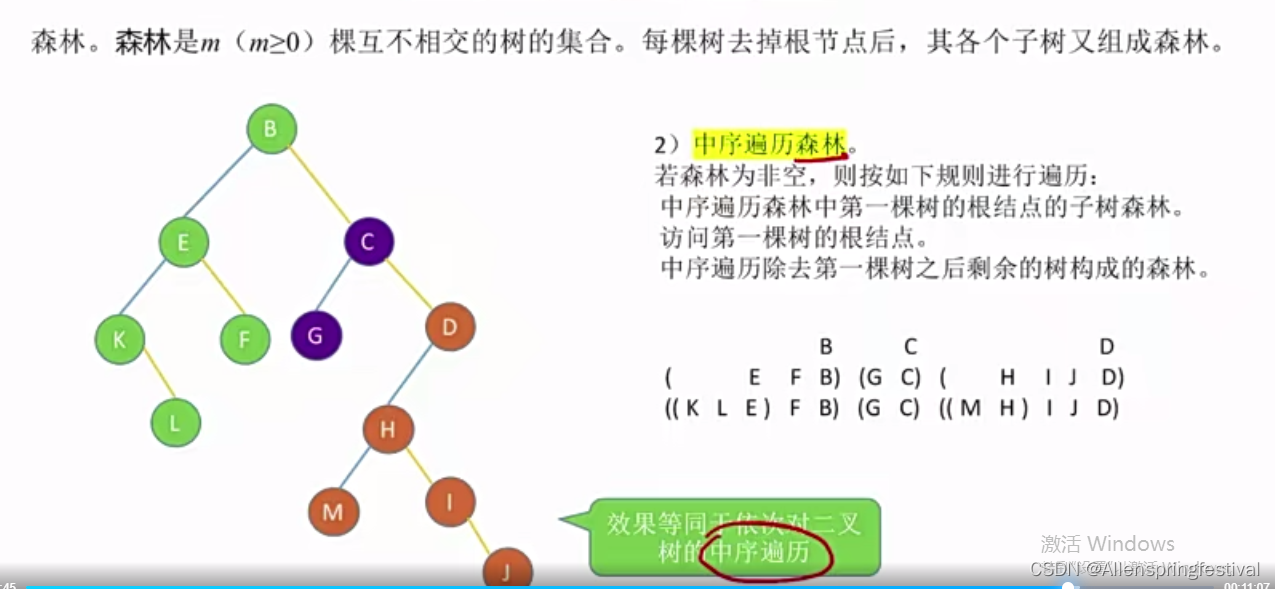
用孩子兄弟表示法,森林可以转换成对应的二叉树,这样就可以实现先序和中序遍历森林。