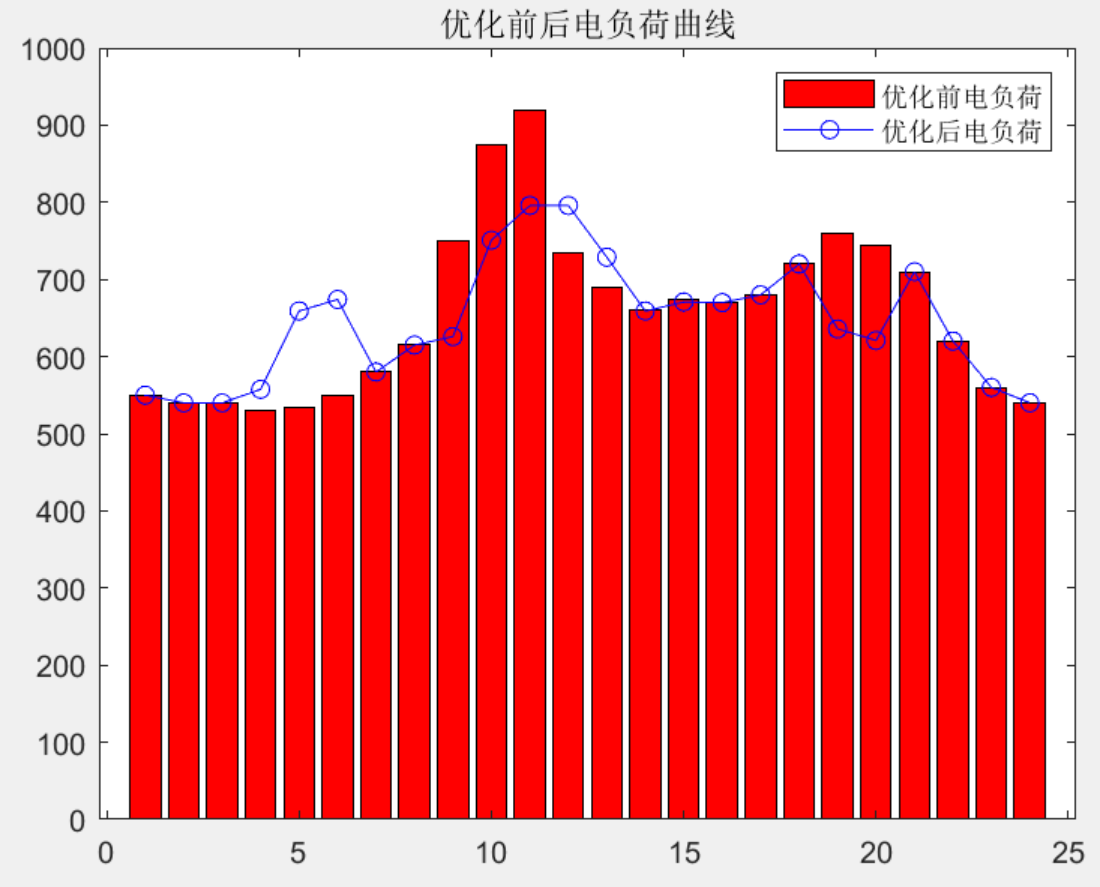
股票中的SMA,EMA和WMA是常用的技术分析指标。这些指标基于历史股价计算得出,可以帮助投资者了解股票的趋势,为决策提供依据。虽然它们都是平均值算法,但它们之间还是有一些区别的。
SMA 简单移动平均线(Simple Moving Average)
SMA是移动平均线的简称,全称是简单移动平均线(Simple Moving Average)。它是历史股价平均值的简单算术平均数。计算SMA,只需要将一段时间内股票收盘价的总和除以这段时间内的交易日数。
例如,计算过去5天的SMA,只需要将这5天的股票收盘价相加,再除以5,即可得出SMA。
SMA是一种较为简单的移动平均方式,经常被用于判断短期的股票趋势。由于SMA只是简单地考虑了过去一段时间的股票价格,因此它会被短期价格波动所影响,因此可能不如其他平均值算法准确。
EMA 指数移动平均线(Exponential Moving Average)
EMA是指数移动平均线(Exponential Moving Average)。与SMA不同,EMA并不是简单的日平均数,而是考虑到股票价格的整体趋势,即将较大的权重放在了最近的股票价格上。
在EMA的计算中,最近的股票价格会得到较高的权重,而较早的股票价格的权重则会下降。计算过程中需要指定EMA的时间周期,通常包括12天和26天等。
对于EMA的计算,需要先计算出一个起始的EMA值。这可以通过计算一段时间内的SMA来得到,然后用下面的计算公式去计算:
当前EMA值 = ((当前收盘价 - 上一个EMA值) * 平滑指数)+ 上一个EMA值
平滑指数可以通过下面的方法来计算:
平滑指数 = 2 /(时间周期 + 1)
EMA的计算方法相对于SMA更为复杂,但它可以更好地反映当前的市场趋势。
y
t
=
x
t
+
(
1
−
α
)
x
t
−
1
+
(
1
−
α
)
2
x
t
−
2
+
.
.
.
+
(
1
−
α
)
t
x
0
1
+
(
1
−
α
)
+
(
1
−
α
)
2
+
.
.
.
+
(
1
−
α
)
t
y_t = \frac{x_t + (1 - \alpha)x_{t-1} + (1 - \alpha)^2 x_{t-2} + ... + (1 - \alpha)^t x_0}{1 + (1 - \alpha) + (1 - \alpha)^2 + ... + (1 - \alpha)^t}
yt=1+(1−α)+(1−α)2+...+(1−α)txt+(1−α)xt−1+(1−α)2xt−2+...+(1−α)tx0
其中,
t
t
t 为窗口大小,
α
\alpha
α 为平滑因子(
0
<
α
≤
1
0 \lt \alpha \leq 1
0<α≤1 可根据公式计算,如
2
/
(
1
+
t
)
2/(1+ t )
2/(1+t),也可自定义),
(
1
−
α
)
i
(1- \alpha) ^ i
(1−α)i 为呈指数增加的权重,期数离预测时刻越近权重越大。
y 0 = x 0 y t = ( 1 − α ) y t − 1 + α x t , \begin{split}\begin{split} y_0 &= x_0\\ y_t &= (1 - \alpha) y_{t-1} + \alpha x_t, \end{split}\end{split} y0yt=x0=(1−α)yt−1+αxt,
# 直接用 Pandas 的ewm 函数
pandas.ewm(span=n)
WMA 加权移动平均线(Weighted Moving Average)
WMA是加权移动平均线(Weighted Moving Average),它是一种考虑过去时间内价格变化和波动的Moving Average方式。与EMA类似,WMA也是将较大的权重放在较近的数据上,但与EMA不同的是,它使用的是带权的平均算法。
在WMA中,每个数据都被通过给定的权重,然后再求和得到加权平均值。通常情况下,较近的数据会有较大的权重,而较远的数据权重会下降,WMA有助于平滑股票价格的波动,并根据相应的趋势给出合适的建议。
WMA的计算也需要指定一个时间周期,并且需要先计算出一段时间内的总权值,用下面的公式计算总权值后,再使用上面的加权平均公式计算WMA:
保存总权值 = 从 1 开始的周期数 * 周期内每个数据的权重之和
每个数据的权重 = (当前周期数 + 1)- 当前数据的位置
WMA是比SMA更为准确的一种移动平均计算方法,但它的计算也更为复杂。
W M A t ( n ) = w 1 x t + w 2 x t − 1 + . . . + w n − 1 x t − n + 2 + w n x t − n + 1 w 1 + w 2 + . . . + w n WMA_t(n) = \frac{w_1x_t + w_2x_{t-1} + ... + w_{n-1}x_{t-n+2} +w_nx_{t-n+1} }{w_1+w_2+ ... + w_n } WMAt(n)=w1+w2+...+wnw1xt+w2xt−1+...+wn−1xt−n+2+wnxt−n+1
其中, n n n为窗口大小, W M A t WMA_t WMAt为t时刻的移动平均值。
技术分析中,权重系数为n~0,即最近一个数值的权重为n,次近的为n-1,如此类推,直到0。
W
M
A
t
(
n
)
=
n
x
t
+
(
n
−
1
)
x
t
−
1
+
.
.
.
+
2
x
t
−
n
+
2
+
x
t
−
n
+
1
n
+
(
n
−
1
)
+
.
.
.
+
2
+
1
WMA_t(n) = \frac{nx_t + (n-1)x_{t-1} + ... + 2x_{t-n+2} +x_{t-n+1} }{n+(n-1)+ ... + 2+1 }
WMAt(n)=n+(n−1)+...+2+1nxt+(n−1)xt−1+...+2xt−n+2+xt−n+1
def WMA(close, n):
weights = np.array(range(1, n+1))
sum_weights = np.sum(weights)
res = close.rolling(window=n).apply(lambda x: np.sum(weights*x) / sum_weights, raw=False)
return res
#或
def WMA(close, n):
return close.rolling(window=n).apply(lambda x: x[::-1].cumsum().sum() * 2 / n / (n + 1))
方法对比分析
从权重思维来看,三种方法都可以认为是加权平均。SMA:权重系数一致;WMA:权重系数随时间间隔线性递减;EMA:权重系数随时间间隔指数递减。 如下图:
下面以 t=30 作图

WMA 是 线性递减,EMA是指数递减

结论
三种平均值算法各有优缺点,你需要根据你的股票市场分析需要及实际情况来决定使用哪种算法。如果你的分析需要考虑。EMA,WMA 即 远离当前时间,影响较小,前一天权重大影响最大。因此在股票很多指标上都用EMA 来代替SMA,如MACD等。