课程概述：

【例题】选择数字

两个参与人A和B，轮流选择[3,4,5,6,7,8,9]中的一个整数（可重复)。当累计总和达到100的时候，博弈结束。此时判所选数字恰好使累计总和达到或超过100的参与人为输家。试问最先行动的A能赢得这场博弈吗?最优策略又是什么?
【解】
整个游戏的过程：

如果前面选择的数字之和能够达到97，98，99的话，那么下一个人最少选择的是3，所以就一定会等于或者超过100。那么这个人就输了。

所以我们如何去控制A每一轮的选择，使得最后一轮该B选择的时候，数字加和已经到达97，98，99，从而使得B一定输呢？
那就是找到每一轮我们可以控制的数。
由于我们观察到我么可选择的数的范围中，两个人选择的数字加和最大是12，也就是我们总可以通过不同的数字组合控制每一轮的加和达到固定的数字12。那么就可以一轮一轮往前推，推到第一轮A应该先手选择什么数字能赢。所以大致思路就是这样的：
据逆推归纳法，当累计接近100时，得到99的A会赢，问题变为抢99。同理，问题可变为抢87[=99-(3+9)]，75，63，51，39，27，15，3，继续逆推，就是先抢到3，会赢。A先选3，则A胜出。

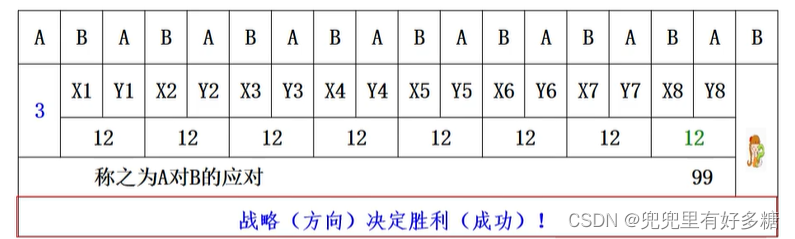
但是如果我们不用上面的战略，第一轮的时候A选择4呢？

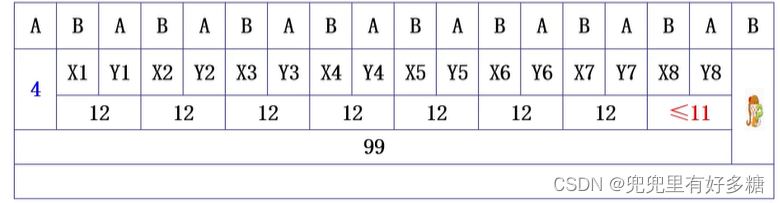
那么一定会导致最后一轮的时候A于B的加和必须小于11，然后轮到B的时候才能是99。但是这是不可控制的，因为一但B选择9，A不论选择什么，这个加和都不可能小于11，所以A直接输掉比赛了。
所以有如下命题：
【命题1】在数字游戏1中，先行动者存在唯一的必胜的最佳应对战略（策略）。

考虑反应对的情形:在本示例中，我们采取的是当A=3时，B选择X1，A再选择Y1，使得X1+Y1=12（我们把这种情形称之为A对B的应对)，进而A能保证赢。如果当A=3时（同学们也可以试试开始时A为其他数字的情形，情况可能有些复杂），B采取A+X1=12，依次Y1+X2=12,…，我们把这种情形称之为B对A的反应对。
但是如果先行动者第一局选择的3，后面都采用和为12的策略，那么B不论做何反应对都是没有用的，B面临的是必输的局面。

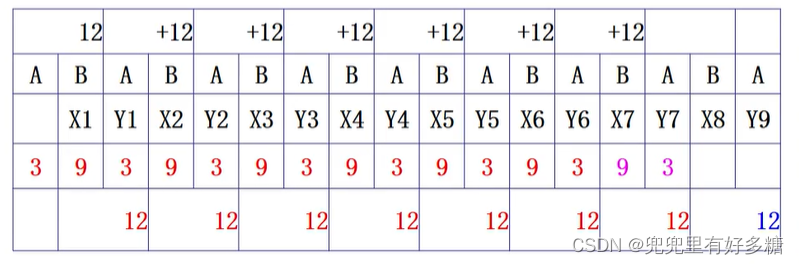
但是如果A一开始没有选择3，而选择的是其他数字，那么B用反应对策略都有唯一的一个机会取胜。
如下图所示，A第一局没有选择3，那么他只能选择比3大的数字，然后B把第一局的加和控制为13，而后面每一局B都使得加和为12，则总和为12*6+13=85。那么在最后一局的时候B只要控制加和为12就是必胜，并且根据A的选择，也可以控制为13或者14，都是必胜的策略。

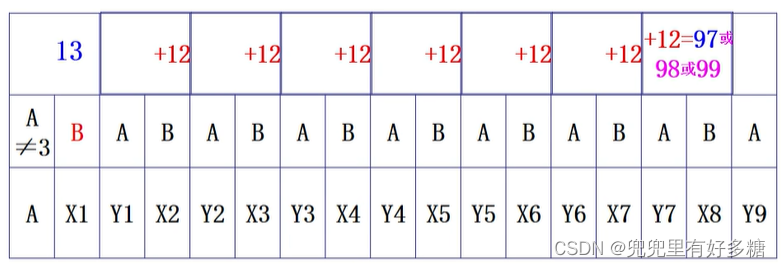
因此又有如下命题：
【命题2】在数字游戏1中，先行动者若开始选择的数字A≠3，则后行动者存在必胜的最佳应对战略（策略），且针对每个不等于3的A，这个战略（策略）是唯一的。

如果达到或超过100的参与人为赢家，局势会怎么样呢?
根据逆推归纳法，当累计接近100时，得到88的人会赢，问题变为抢88。同理，问题可变为抢76，64，52，40，28，16，4,继续逆推（
100-12n，当n=8时余4），就是先抢到4的人会赢。先行动的A先选4，则A胜出。

【例题】巴什博弈

一堆石子有n颗，A、B两个人轮流拿取，每次至少拿取1颗，至多拿取m颗，拿走最后一颗石子的人获胜。
【解】
假设石子有 n=m+1由于一次只能取m颗，无论先手取多少颗，后手总能拿走剩余的，这时一定是先手负。
若石子n= (m+1)*r+s，对于先手应该先取走s颗，设后手取走k颗，先手再取走m+1-k，剩余的石子颗数为(m+1)(r-1)以后保持这样的取法，先取者获胜。总之，就是要留给对手m+1的倍数。
【命题3】在巴什博弈中，如果石子数量n%(m + 1)=0 时，后手胜;如果石子数量n%(m + 1)≠0时，先手胜。

【例题】射手博弈

射手A、B、C以抽签的方式决定轮流开枪的顺序并进行决斗，A的命中率为100%，B的命中率为80%，C的命中率为50%。
(1）若按顺序进行且C首先开枪射击，他应该怎样做?
(2)如果按顺序进行射击，证明C存活的可能性最大。
(3）若每一轮开枪的人是任意选择的，证明射手存活的概率与命中率完全相反

【解】
追求的目标一定是两个：首先是考虑保命，然后再考虑射击谁。
(1)若按顺序进行且C首先开枪射击，他应该怎样做?
设${\pi }_A(ABC)$表示三人都活着，且按ABC顺序射击时A存活的概率，其余表示含义类似。
①如果C射击其他人，一定是射击A。（因为首先要考虑保命，所以一定会优先射击那个命中率高的人)
如果C击中A，那么他的支付为${\pi }_C(BC)$。
因为在BC这个顺序下C存活的概率取决于B的命中率，如果B把C打中了，那么C存活概率就是0，打所以这种情况下C的存活概率是$\frac{4}{5}\ast 0=0$，如果没有打中的话（概率是$\frac{1}{5}$），就该C打B了。
所以有式子：${\pi }_C(BC)={\pi }_C(CB)/5$
而$${\pi }_C(CB)=\frac{1}{2}\times 1+\frac{1}{2}\times {\pi }_C(BC)=\frac{1}{2}\times 1+\frac{1}{2}\times \frac{1}{5}{\pi }_C(CB)$$
于是可得：
$${\pi }_C(CB)=\frac{5}{9},{\pi }_C(BC)=\frac{1}{9}(C击中A，C存活的概率)$$
没有击中A的情况如②:
②如果C射向空中。显然A将射向B而不是C，并且B将会射向A而不是C。(因为首先要考虑保命，所以一定会优先射击那个命中率高的人）。因而A和B将会互相射击，直到其中一个人出局，接着该轮到C射击了。

若A是A、B互相射击的幸存者，则此时C幸存的概率为${\pi }_C(CA)=\frac{1}{2}$。
若B是A、B互相射击的幸存者，则此时C幸存的概率是${\pi }_C(CB)=\frac{5}{9}$。
因为${\pi }_C(CB)=\frac{5}{9}$，${\pi }_C(CA)=\frac{1}{2}$，均大于${\pi }_C(BC)=\frac{1}{9}$。所以C射向空中是其最优选择。
(2)如果按顺序进行射击，证明C存活的可能性最大。
证明:①假设A在B之前射击，顺序可能为CAB或ACB或ABC三种可能。
因为C射向空中，A一定确保能干掉B，所以
$${\pi }_C(CAB)={\pi }_C(ACB)={\pi }_C(ABC)=\frac{1}{2}$$
于是可得：
$${\pi }_A(CAB)={\pi }_A(ACB)={\pi }_A(ABC)=\frac{1}{2}$$
②假设B在A之前射击，顺序为CBA或BCA或BAC三种可能。那么B就会射向A，击中的概率为4/5，因而
$$\begin{array}{rl}{\pi }_C(CBA)& ={\pi }_C(BCA)={\pi }_C(BAC)\\ & =\frac{4}{5}{\pi }_C(CB)+\frac{1}{5}{\pi }_C(CA)\\ & =\frac{4}{5}\times \frac{5}{9}+\frac{1}{5}\times \frac{1}{2}=\frac{49}{90}\end{array}$$
此外
$$\begin{array}{rl}{\pi }_A(CBA)={\pi }_A(BCA)={\pi }_A(BAC)& \\ =\frac{4}{5}\times 0+\frac{1}{5}\times \frac{1}{2}=\frac{1}{10}& \\ {\pi }_B(CBA)& =\frac{4}{5}\times \frac{4}{9}+\frac{1}{5}\times 0=\frac{16}{45}\end{array}$$

(3）若每一轮开枪的人是任意选择的，证明存活率与命中率完全相反。
【证明】设${\pi }_A[A]$表示A开第一枪时A幸存概率，${\pi }_A$表示A总体幸存概率， π A { A B } \pi_A\left\{AB\right\} πA​{AB}表示AB两人谁开第一枪是任意的。其余类似表示。
如果下一轮进行射击的选手任意选择，结果依然是A和B将会互相射击直到两人中只有一人幸存。无论如何，显然C更愿意与B一对一较量而不是与A，所以C有机会射击的话将会射向A。
现在分析两个人的情形:
π A { A B } = 1 2 × 1 + 1 2 × 1 5 π A { A B } π A { A B } = 5 9 , π B { A B } = 4 9 \begin{aligned} & \pi_A\{A B\}=\frac{1}{2} \times 1+\frac{1}{2} \times \frac{1}{5} \pi_A\{A B\} \\ & \pi_A\{A B\}=\frac{5}{9}, \quad \pi_B\{A B\}=\frac{4}{9} \end{aligned} ​πA​{AB}=21​×1+21​×51​πA​{AB}πA​{AB}=95​,πB​{AB}=94​​
以此类推：
π A { A C } = 1 2 × 1 + 1 2 × ( 1 2 × π A { A C } ) \pi_A\{A C\}=\frac{1}{2} \times 1+\frac{1}{2} \times\left(\frac{1}{2} \times \pi_A\{A C\}\right) πA​{AC}=21​×1+21​×(21​×πA​{AC})
于是有 π A { A C } = 2 3 , π C { A C } = 1 3 \pi_A\{A C\}=\frac{2}{3}, \pi_C\{A C\}=\frac{1}{3} πA​{AC}=32​,πC​{AC}=31​
进而有：
π B { B C } = 1 2 × [ 4 5 × 1 + 1 5 π B { B C } ] + 1 2 × 1 2 π B { B C } \pi_B\{B C\}=\frac{1}{2} \times\left[\frac{4}{5} \times 1+\frac{1}{5} \pi_B\{B C\}\right]+\frac{1}{2} \times \frac{1}{2} \pi_B\{B C\} πB​{BC}=21​×[54​×1+51​πB​{BC}]+21​×21​πB​{BC}
π B { B C } = 8 13 π C { B C } = 5 13 \begin{aligned} & \pi_B\{B C\}=\frac{8}{13} \\ & \pi_C\{B C\}=\frac{5}{13} \end{aligned} ​πB​{BC}=138​πC​{BC}=135​​
现在，显然：
π A [ A ] = π A { A C } = 2 3 , π B [ A ] = 0 , π C [ A ] = 1 3 \pi_A[A]=\pi_A\{A C\}=\frac{2}{3}, \pi_B[A]=0, \pi_C[A]=\frac{1}{3} πA​[A]=πA​{AC}=32​,πB​[A]=0,πC​[A]=31​
同样, 容易得到
π B [ B ] = 4 5 π B { B C } + 1 5 π B , π A [ B ] = 1 5 π A π C [ B ] = 4 5 π C { B C } + 1 5 π C  和  π C [ C ] = 1 2 π C { B C } + 1 2 π C , π A [ C ] = 1 2 π A π B [ C ] = 1 2 π B { B C } + 1 2 π B \begin{aligned} & \pi_B[B]=\frac{4}{5} \pi_B\{B C\}+\frac{1}{5} \pi_B, \pi_A[B]=\frac{1}{5} \pi_A \\ & \pi_C[B]=\frac{4}{5} \pi_C\{B C\}+\frac{1}{5} \pi_C \\ & \text { 和 } \pi_C[C]=\frac{1}{2} \pi_C\{B C\}+\frac{1}{2} \pi_C, \pi_A[C]=\frac{1}{2} \pi_A \\ & \pi_B[C]=\frac{1}{2} \pi_B\{B C\}+\frac{1}{2} \pi_B \end{aligned} ​πB​[B]=54​πB​{BC}+51​πB​,πA​[B]=51​πA​πC​[B]=54​πC​{BC}+51​πC​ 和 πC​[C]=21​πC​{BC}+21​πC​,πA​[C]=21​πA​πB​[C]=21​πB​{BC}+21​πB​​
合并到一起计算，于是得到：
π A = 1 3 [ 2 3 + 1 5 π A + 1 2 π A ] → π A = 20 69 π B = 1 3 [ 0 + 4 5 π B { B C } + 1 5 π B + 1 2 π B { B C } + 1 2 π B ] → π B = 24 69 π C = 1 3 [ 1 3 + 4 5 π C { B C } + 1 5 π C + 1 2 π C { B C } + 1 2 π C ] → π C = 25 69 \begin{aligned} & \pi_A=\frac{1}{3}\left[\frac{2}{3}+\frac{1}{5} \pi_A+\frac{1}{2} \pi_A\right] \rightarrow \pi_A=\frac{20}{69} \\ & \pi_B=\frac{1}{3}\left[0+\frac{4}{5} \pi_B\{B C\}+\frac{1}{5} \pi_B+\frac{1}{2} \pi_B\{B C\}+\frac{1}{2} \pi_B\right] \rightarrow \pi_B=\frac{24}{69} \\ & \pi_C=\frac{1}{3}\left[\frac{1}{3}+\frac{4}{5} \pi_C\{B C\}+\frac{1}{5} \pi_C+\frac{1}{2} \pi_C\{B C\}+\frac{1}{2} \pi_C\right] \rightarrow \pi_C=\frac{25}{69} \end{aligned} ​πA​=31​[32​+51​πA​+21​πA​]→πA​=6920​πB​=31​[0+54​πB​{BC}+51​πB​+21​πB​{BC}+21​πB​]→πB​=6924​πC​=31​[31​+54​πC​{BC}+51​πC​+21​πC​{BC}+21​πC​]→πC​=6925​​
于是有
$${\pi }_C>{\pi }_B>{\pi }_A$$
得证。
（视频是2.23第一节）

博弈论的基本概念：

博弈论的基本概念:参与人、战略、行动、信息、支付函数、均衡结果等。

• 要素（PAPI):博弈主体（参与人）、战略(行动）、支付、信息。
• 规则:参与人、行动次序、均衡结果。

参与人

独立决策、独立行动并承担结果的个人或组织。
“自然”:“虚拟参与人”
根据参与人数分:

• 单人博弈
• 两人博弈
• 多人博弈

战略

行动

信息

支付函数

【例题】分100元

两个人各报一个至多为100的非负整数。若所报的数字之和不超过100，则每人得到所报的钱数（多余的钱充公)﹔若两人所报的数字之和超过100且数目不同，则报较小数的人得到白己所报的钱数，而另一个人则得到剩余的钱;若两人所报的数字之和超过100且数目相同，则每个人得到50元。

【解】博弈三要素:
参与人集合： N = { 1 , 2 } N=\left\{1,2\right\} N={1,2}
战略集合： S t = { 0 , 1 , 2... , 100 } , t = 1 , 2 S_t=\left\{0,1,2...,100\right\},t=1,2 St​={0,1,2...,100},t=1,2
参与人$i$的支付：
$$u_i=\{\begin{array}{ll}{s}_i& \text{ 当 }{s}_i+s_j\le 100(i,j=1\text{ 或 }2)\\ s_i& \text{ 当 }{s}_i+s_j>100,\text{ 且 }{s}_i<s_j\\ 100-s_j& \text{ 当 }{s}_i+s_j>100,\text{ 且 }{s}_i>s_j\\ 50& \text{ 当 }{s}_i+s_j>100,\text{ 且 }{s}_i=s_j\end{array}$$