Hausdorff距离量度度量空间中紧子集之间的距离
定义
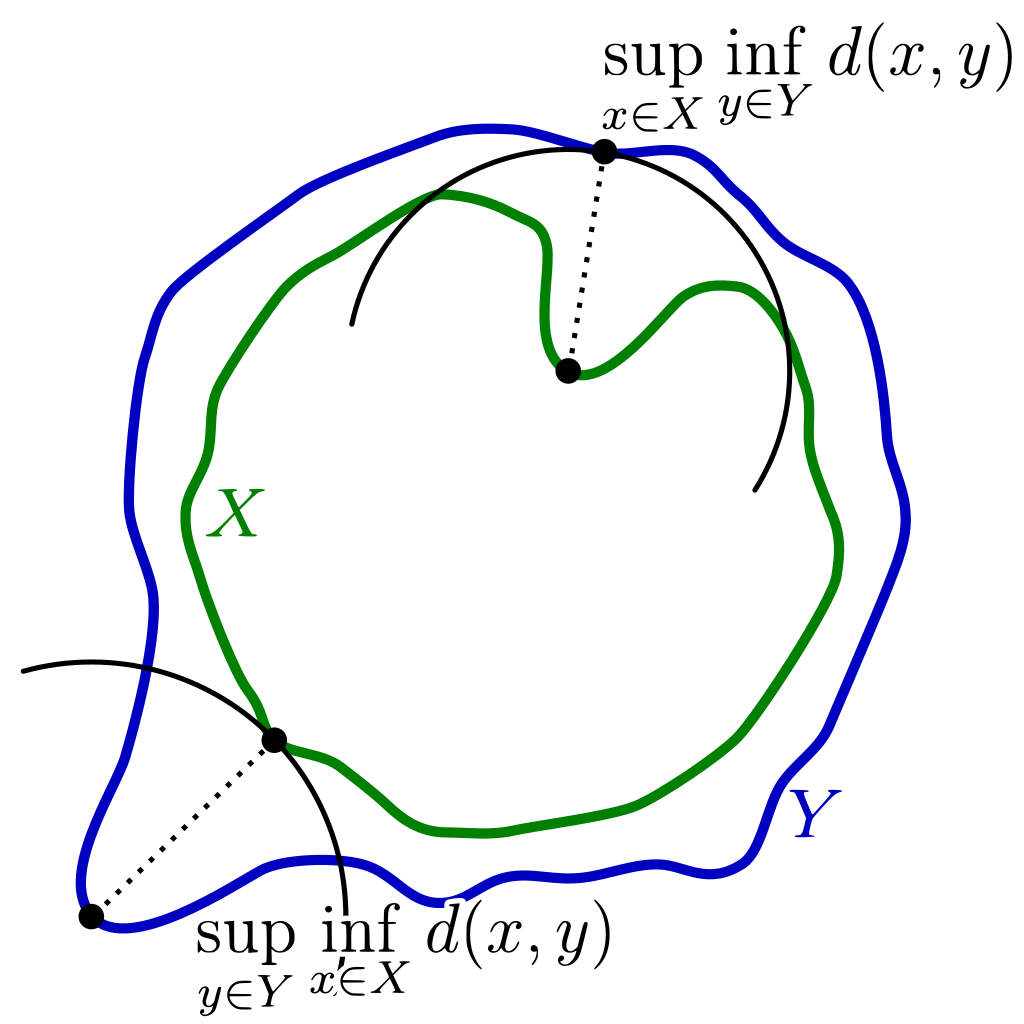
设
X
X
X和
Y
Y
Y是度量空间
M
M
M的两个紧子集
d
H
(
X
,
Y
)
=
max
{
sup
x
∈
X
inf
y
∈
Y
d
(
x
,
y
)
,
sup
y
∈
Y
inf
x
∈
X
d
(
x
,
y
)
}
d_H\left(X, Y\right) = \max \left\{\sup_{x\in X} \inf_{y\in Y} d\left(x, y\right), \sup_{y\in Y} \inf_{x\in X} d\left(x, y\right)\right\}
dH(X,Y)=max{x∈Xsupy∈Yinfd(x,y),y∈Ysupx∈Xinfd(x,y)}
实现方式
图像中
假设有两个二值图像 X , Y \mathbf{X}, \mathbf{Y} X,Y,先计算 sup x ∈ X inf y ∈ Y d ( x , y ) \sup_{x\in X} \inf_{y\in Y} d\left(x, y\right) supx∈Xinfy∈Yd(x,y)
首先找到两张图像的边缘,因为找的
sup
\sup
sup,而边缘肯定距离更大
具体实现方式为,先腐蚀,然后和原图像异或
接着计算
Y
~Y
Y的Distance transform,得到的结果是
Y
\mathbf{Y}
Y中所有的点到最近的
0
0
0的距离
这一步具体可以看参考里的链接,如果
d
d
d是欧氏距离,计算的时间复杂度是
O
(
∣
X
∣
)
O\left(\left|X\right|\right)
O(∣X∣)
然后根据
X
X
X,就可以得到所有点的
inf
y
∈
Y
d
(
x
,
y
)
\inf_{y\in Y} d\left(x, y\right)
infy∈Yd(x,y)
最后取
sup
\sup
sup就行了
如果最后取得不是 sup \sup sup而是某个分位点,比如95,拿得到得就是单边得 H D 95 HD95 HD95了
https://zhuanlan.zhihu.com/p/153137266?from_voters_page=true
Distance Transforms of Sampled Functions
A GENERAL ALGORITHM FOR COMPUTING DISTANCE TRANSFORMS IN LINEAR TIME
https://cs.stackexchange.com/questions/117989/hausdorff-distance-between-two-binary-images-according-to-distance-maps