目录
- 一、指纹图像预处理
- 1.1 图像对比度增强
- 1.2 图像二值化
- 1.3 图像滤波
- 二、指纹图像特征提取
指纹识别系统主要涉及4个步骤:指纹图像采集、图像预处理、特征提取、特征匹配。一开始,通过指纹读取设备取得图像,并对原始图像进行初步处理,使之更清晰。接下来,指纹识别软件提取指纹的数字表示——特征点数据。这些数据通常称为模板,保存为数据库中的一条记录并录入相应的人员信息。随后,对新录入指纹进行特征点数据的提取,并通过计算机模糊比较的方法把它与指纹数据库中的模板进行比较,计算出它们的相似程度,最终得到匹配结果并显示人员信息。
一、指纹图像预处理
1.1 图像对比度增强
采集到的指纹存在噪声干扰等问题,因此在指纹识别及指纹信息录入时必须进行必要的图像预处理。在图像去噪中,中值滤波器是一种常见的非线性平滑滤波器,中值滤波器的输出像素是由邻域像素的中间值决定的。中值滤波器产生的模数较少,适合于消除图像的孤立噪声点,直接调用MATLAB工具箱中的medfilt2()函数。在图像增强方面,进行直接灰度调整以增强指纹图像的对比度,调用MATLAB 工具箱中的imadjust()函数。程序如下:
A=imread('a.bmp');
A=rgb2gray(A);
j=medfilt2(A);
figure,imshow(j);
B=imadjust(A,[0.2 0.8]);
figure;
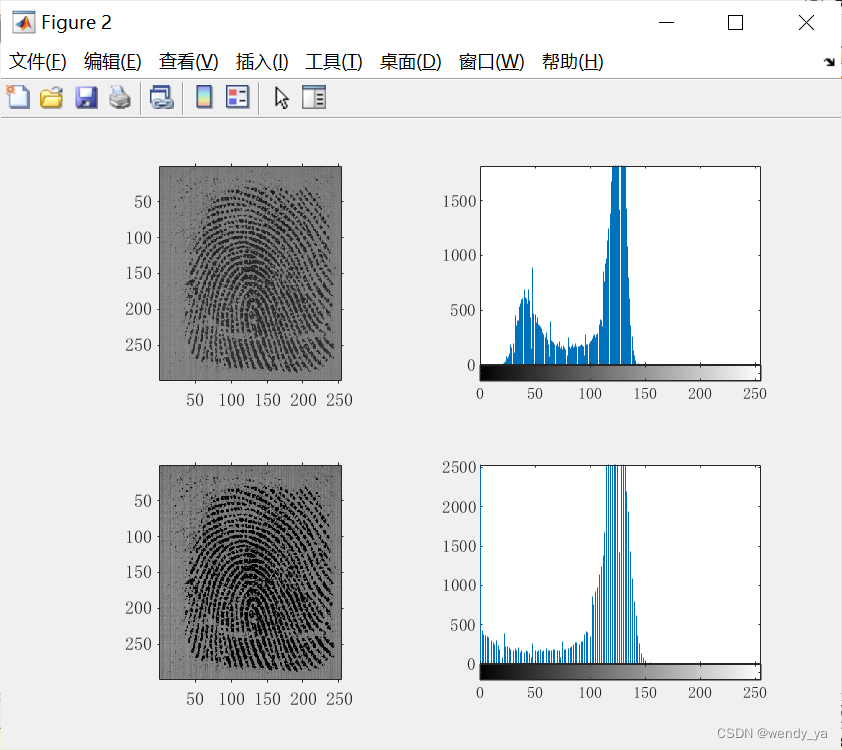
subplot(2,2,1);imshow(A);
subplot(2,2,2);imhist(A);
subplot(2,2,3);imshow(B);
subplot(2,2,4);imhist(B);
运行结果如下:
1.2 图像二值化
图像二值化:采用迭代法求最佳阈值的分割算法,具体步骤如下:
①求出图像中的最大和最小灰度值
S
1
S_1
S1、
S
h
S_h
Sh,令初始阈值为:
T
0
=
S
1
+
S
h
2
T_0=\frac{S_1+S_h}{2}
T0=2S1+Sh
②根据阈值
T
k
T_k
Tk将灰度图像分成目标和背景两部分(第一次分割时
T
k
=
T
0
T_k=T_0
Tk=T0),然后求出目标和背景两部分的平均灰度值
S
1
S1
S1、
S
2
S2
S2:
S
1
=
∑
S
(
i
,
j
)
p
T
k
S
(
i
,
j
)
×
N
(
i
,
j
)
∑
Z
(
i
,
j
)
p
T
k
N
(
i
,
j
)
,
S
2
=
∑
S
(
i
,
j
)
f
T
k
S
(
i
,
j
)
×
N
(
i
,
j
)
∑
Z
(
i
,
j
)
f
T
k
N
(
i
,
j
)
{S_1} = \frac{{\sum\limits_{S(i,j)p{T_k}} {S(i,j) \times N(i,j)} }}{{\sum\limits_{Z(i,j)p{T_k}} {N(i,j)} }},{S_2} = \frac{{\sum\limits_{S(i,j)f{T_k}} {S(i,j) \times N(i,j)} }}{{\sum\limits_{Z(i,j)f{T_k}} {N(i,j)} }}
S1=Z(i,j)pTk∑N(i,j)S(i,j)pTk∑S(i,j)×N(i,j),S2=Z(i,j)fTk∑N(i,j)S(i,j)fTk∑S(i,j)×N(i,j)
式中,
S
(
i
,
j
)
S(i,j)
S(i,j)是图像上(i,j)点的灰度值,
N
(
i
,
j
)
N(i,j)
N(i,j)是(i,j)点的权重系数,一般
N
(
i
,
j
)
=
1
,
0
N(i,j)=1,0
N(i,j)=1,0。
③求出新的阈值:
T
k
+
1
=
S
1
+
S
2
2
T_{k+1}=\frac{S_1+S_2}{2}
Tk+1=2S1+S2
具体程序如下:
[x,y]=size(B);
m=double(B);
N=sqrt(100)*randn(x,y);
I=m+N;
for i=1:x
for j=1:y
if (I(i,j)>255)
I(i,j)=255;
end
if (I(i,j)<0)
I(i,j)=0;
end
end
end
z0=max(max(I));
z1=min(min(I));
T=(z0+z1)/2;
TT=0;
s0=0;n0=0;
s1=0;n1=0;
allow=0.5;
d=abs(T-TT);
count=0;
while(d>=allow)
count=count+1;
for i=1:x
for j=1:y
if(I(i,j)>=T)
s0=s0+I(i,j);
n0=n0+1;
end
if(I(i,j)<T)
s1=s1+I(i,j);
n1=n1+1;
end
end
end
T0=s0/n0;
T1=s1/n1;
TT=(T0-T1)/2;
d=abs(T-TT);
T=TT;
end
seg=zeros(x,y);
for i=1:x
for j=1:y
if(I(i,j)>=T)
seg(i,j)=1;
end
end
end
figure;
imshow(seg);
运行结果如下:

1.3 图像滤波
得到二值化图像后,需要对其进行进一步滤波增强,程序如下:
BW1=bwmorph(seg,'spur');
BW2=bwmorph(BW1,'fill');
BW3=bwmorph(BW2,'clean');
figure;
imshow(BW3);
滤波结果如图所示:

二、指纹图像特征提取
纹理特征提取指的是通过一定的图像处理技术抽取出图像的纹理特征,从而获得纹理的定性或定量描述的处理过程。因此,纹理特征提取包括两方面的内容:检测出纹理基元和获得有关纹理基元排列分布方式的信息。纹理分析方法大致分为统计方法和结构方法。统计方法适用于分析像木纹、森林、山脉、草地那样的纹理细而且不规则的物体,结构方法则适用于像布料的印刷图案或砖花样等一类纹理基元排列较规则的图像。针对指纹图像,这里选择灰度共生矩阵法提取指纹纹理特征。
从灰度共生矩阵提取出的纹理特征参数有角二阶矩、对比度、相关和熵,这四个统计参数为应用灰度共生矩阵进行纹理分析的主要参数,可以组合起来成为纹理分析的特征参数使用。利用graycomatrix和graycoprops函数实现。
glcms = graycomatrix(I,Name,Value)
从图像 I 创建灰度共生矩阵 (GLCM)。灰度共生矩阵又名灰度空间相关性矩阵。
根据可选名称-值对Name,Value组参数的值,返回一个或多个灰度共生矩阵。
graycomatrix 通过计算灰度级(灰度强度)值为 I 的像素与灰度级值为 j 的像素水平相邻的频率来创建 GLCM。(您可以使用 ‘Offsets’ 参数指定其他像素空间关系。)glcm 中的每个元素 (i,j) 指定值为 i 的像素与值为 j 的像素水平相邻的次数。
stats = graycoprops(glcm,properties)
根据灰度共生矩阵glcm计算properties中指定的统计信息。
运行结果:
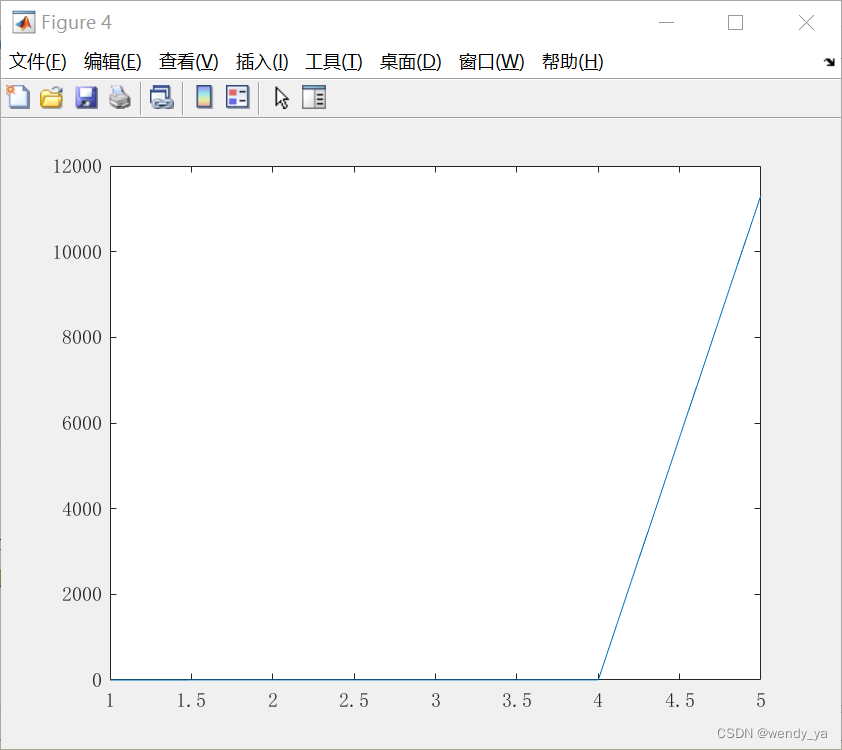
同样,以此方法求出员工的指纹图像的纹理特征,与数据库内指纹的这一特征进行比较,并以最小距离分类器的原理进行比较判断即可得出准确的员工信息并标注显示。
未完待续…