标题：Self-supervised Co-training for Video Representation Learning
会议：NIPS2020
论文地址：https://dl.acm.org/doi/abs/10.5555/3495724.3496201
官方代码：https://www.robots.ox.ac.uk/~vgg/research/CoCLR/
作者单位：牛津大学

Abstract

本文的研究目标是纯视觉的自监督视频表征学习。我们做出了以下贡献：①我们研究了在基于实例的信息噪声对比估计（Info Noise Contrastive Estimation，InfoNCE）训练中加入语义类别正样本的好处，表明了这种形式的有监督对比学习带来了明显的性能提升；②我们提出了一种新颖的自监督协同训练方案来改进流行的infoNCE损失，利用同一数据源的不同视图，RGB流（RGB streams）和光流（optical flow）的互补信息，通过使用一个视图来获得另一个视图的正类样本；③我们在两个不同的下游任务：动作识别（action recognition）和视频检索（video retrieval）上全面评估了学习到的表征的质量。在这两种情况下，所提出的方法都表现出与其它自监督方法SOTA或可比的性能，同时训练效率明显更高，即只需要远远更少的训练数据就能达到类似的性能。

1 Introduction

最近，在图像和视频的自监督表征学习方面的进展已经证明了在数据样本上使用判别性对比损失的好处，例如NCE。给定一个数据样本，目标是将其变换后的版本与数据集中的其它样本进行区分。这些变换可以是人工的，如数据增强中使用的变换，也可以是自然的，如来自同一短片（clip）内的时间段的视频中出现的变换。从本质上讲，这些代理任务（pretext tasks）聚焦于实例判别（instance discrimination）：将每个数据样本视为一个“类别”，目标是从大量其它数据样本或其数据增强版本中判别出自己的数据增强版本。以这种方式通过实例判别学习到的表征在下游任务上表现出极高的性能，通常能与通过有监督训练达到的性能相当。
在本文中，我们以自监督视频表征学习为目标，提出问题：实例判别是否充分利用了数据？ 我们从两个方面证明了答案是否定的：
首先，我们证明了在自监督训练中难正样本被忽略，如果包含这些难正样本，那么学习到的表征质量会显著提高。为了研究这一点，我们进行了一个oracle实验，其根据语义类别标签来将正样本纳入到基于实例的训练过程中。可以观察到纯基于实例的学习（称为InfoNCE）与oracle版本（称为UberNCE）之间存在明显的性能差距。注意，该oracle是有监督对比学习的一种形式，因为它鼓励特征表示根据类别标签线性可分。在我们的实验中，使用UberNCE的训练实际上要优于使用交叉熵训练的有监督模型，这一现象在图像分类的同期工作中也观察到了。
其次，我们提出了一种自监督的协同训练方法，称为CoCLR，代表“视觉表征的协同训练对比学习”，其目标是利用数据的其它互补视图来挖掘正样本，即替代oracle的作用。我们在此选择RGB视频帧和光流作为两个视图。如图1所示，从流中获得的正样本可以用来弥补RGB视频短片实例之间的差距。反过来，从RGB视频短片中获得的正样本可以关联相同动作的光流短片。使用CoCLR算法训练的结果是一个显著超过使用InfoNCE基于实例训练得到的性能，并且接近使用UberNCE进行oracle训练的性能的表征。

需要说明的是，这里我们并没有提出一个新的损失函数或代理任务，而是面向训练机制，改进视觉表征对比学习中的采样过程，即构建实例之外的正样本对。这样有两个好处：首先，训练中使用了同一类别（如图1所示的高尔夫挥杆动作）的（难）正样本；其次，这些正样本从实例级的负样本中被移除——它们在这种情况下会被当作动作类别的假负样本。本文的主要兴趣是利用另一个视图提供的互补信息来改进RGB网络和Flow网络的表征。对于推理，我们可以选择只使用RGB网络或Flow网络，或者两者都使用，这取决于应用和效率要求。
综上所述，我们研究了从RGB帧、无监督的光流或两者结合学习到的纯视觉的自监督视频表征，并做出了以下贡献：①我们证明了一个具有语义类别标签的oracle提高了基于实例的对比学习的性能；②我们提出了一种新颖的自监督协同训练方案CoCLR，以改进流行的InfoNCE的训练机制，利用来自同一数据源不同视图的互补信息；③我们在UCF101和HMDB51上对视频动作识别和检索两个下游任务上学习到的表征质量进行了全面评估。在所有情况下，我们证明了与其它自监督方法相比SOTA或相当的性能，同时效率明显更高，即自监督预训练所需的数据更少。
我们观察到，本文中用来弥补RGB来自同一类别正样本之间差距的第二个互补视图是光流。然而，该思想一般也适用于其它的互补视图：对于视频而言，音频或文本解说可以起到类似光流的作用；而对于静止图像，通过不同的滤波器传播图像可以形成多个视图。

2 Related work

纯视觉的自监督学习。 近年来，自监督视觉表征学习在图像分类领域取得了快速发展。该领域的早期工作显式定义了代理任务，例如着色、修补和拼图求解。最近的一些方法联合优化聚类和表征学习或者通过对比学习区分不同的实例来学习视觉表征。视频提供了额外的机会来学习表征，除了图像还可以通过利用时空信息，例如通过排序帧或短片、动作、co-occurrence、拼图，旋转，速度预测，未来预测，或通过时间一致性。
多模态自监督学习。 该研究领域侧重于利用不同模态的相互作用，例如，对比损失被用来学习帧与音频，或视频与解说之间的关联；或者，Alwassel等人使用了一种视频和音频的迭代聚类和重标注方法。
协同训练成对的网络。 协同训练是指一种半监督学习技术，它假设每个实例由多个视图描述，这些视图提供了关于实例的不同和互补的信息。协同训练首先使用任一有标签的样本为每个视图学习一个单独的分类器，然后使用每个分类器对未标注数据置信度最高的预测来迭代地构建额外的有标签的训练数据。尽管在我们的情况中注意到我们没有带标签的样本。更一般地，两个网络相互影响和协同训练的思想也出现在机器学习的其它领域，例如生成式对抗网络（GANs）和演员-评论家强化学习（Actor-Critic Reinforcement Learning）。
视频动作识别。 该研究领域近年来经历了快速发展，从双流网络到最近的单流RGB网络，动作分类的性能稳步提升。特别地，蒸馏的使用，其中在高层上flow-stream网络被用于教RGB-stream网络，与本工作的目标有关。

3 InfoNCE, UberNCE and CoCLR

我们首先回顾了使用InfoNCE的基于实例判别的自监督学习，并引入了一个oracle扩展，其根据语义类别标签来将正样本纳入到基于实例的训练过程中。然后，我们介绍了使用多视图协同训练挖掘提供有用信息的正样本对的关键思想，并描述了我们使用它的算法，这使得InfoNCE能够扩展到实例判别之外。

3.1 Learning with InfoNCE and UberNCE

InfoNCE。 给定一个包含$N$个原始视频短片的数据集，例如 D = { x 1 , x 2 , . . . , x N } \mathcal{D}=\{x_1,x_2,...,x_N\} D={x1​,x2​,...,xN​}，自监督视频表征学习的目标是获得一个函数$f(\cdot )$，该函数可以有效地用于编码视频短片用于各种下游任务，例如动作识别、检索等。
假设存在一个增强函数$\psi (\cdot ;a)$，其中$a$是从一组预定义的数据增强变换$A$中采样，并应用于$\mathcal{D}$。对于某一样本$x_i$，正样本集合${\mathcal{P}}_i$和负样本集合${\mathcal{N}}_i$的定义为： P i = { ψ ( x i ; a ) ∣ a ∼ A } \mathcal{P}_i=\{\psi(x_i;a)|a\sim A\} Pi​={ψ(xi​;a)∣a∼A}和 N i = { ψ ( x n ; a ) ∣ ∀ n ≠ i , a ∼ A } \mathcal{N}_i=\{\psi(x_n;a)|\forall n\neq i,a\sim A\} Ni​={ψ(xn​;a)∣∀n=i,a∼A}，则InfoNCE损失为：
$${\mathcal{L}}_{\mathrm{InfoNCE}}=-\mathbb{E}\left[\log \frac{\exp (z_i\cdot z_p/\tau )}{\exp (z_i\cdot z_p/\tau )+{\sum }_{n\in {\mathcal{N}}_i}\exp (z_i\cdot z_n/\tau )}\right]\text{\hspace{1em}(1)}$$其中，$z_i\cdot z_p$表示两个向量之间的点积。本质上，优化的目标可以看作是实例判别，即在同一实例的增强视图之间比在其它实例的增强视图之间发出更高的相似性分数。
UberNCE。 假设我们有一个带有标注的数据集，$\mathcal{D}=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}$，其中$y_i$是短片$x_i$的类标签，并且有一个能够使用这些标注的oracle。我们通过优化与公式1相同的InfoNCE来寻找函数$f(\cdot )$，除了每个样本$x_i$之外，正样本集合${\mathcal{P}}_i$和负样本集合${\mathcal{N}}_i$现在可以包括具有相同语义标签的样本，还有其增强，即 P i = { ψ ( x i ; a ) , x p ∣ y p = y i   a n d   p ≠ i , ∀ p ∈ [ 1 , N ] , a ∼ A } \mathcal{P}_i=\{\psi(x_i;a),x_p|y_p=y_i~\mathrm{and}~p\neq i,\forall p\in[1,N],a\sim A\} Pi​={ψ(xi​;a),xp​∣yp​=yi​ and p=i,∀p∈[1,N],a∼A}， N i = { ψ ( x n ; a ) , x n ∣ y n ≠ y i , ∀ n ∈ [ 1 , N ] , a ∼ A } \mathcal{N}_i=\{\psi(x_n;a),x_n|y_n\neq y_i,\forall n\in[1,N],a\sim A\} Ni​={ψ(xn​;a),xn​∣yn​=yi​,∀n∈[1,N],a∼A}。
例如，给定一个“跑步”动作的输入视频短片，正样本集合包含其自身的增强版本和数据集中所有其它“跑步”的视频短片，负样本集合包含来自其它动作类别的所有视频短片。
如第4.4节所证明的，我们评估了linear probe协议上的表征，并观察到使用InfoNCE和UberNCE的训练之间存在显著的性能差距，证实了实例判别并没有充分利用数据。显然，选择采样信息更丰富的正样本，即把语义相关的短片作为正样本对（从而自然地消除了假负样本），在这种表征学习中起着至关重要的作用，因为这是InfoNCE和UberNCE的唯一区别。

3.2 Self-supervised CoCLR

作为先前符号的扩展，给定一个视频短片$x_i$，我们现在考虑两个不同的视图， x i = { x 1 i , x 2 i } x_i=\{x_{1i},x_{2i}\} xi​={x1i​,x2i​}，其中，$x_{1i}$和$x_{2i}$在本文分别表示RGB帧及其无监督光流。自监督视频表征学习的目标是学习函数$f_1(\cdot )$和$f_2(\cdot )$，其中$z_{1i}=f_1(x_{1i})$和$z_{2i}=f_2(x_{2i})$表示RGB流和光流的表征，可以有效地用于执行各种下游任务。
该方法区别于InfoNCE和UberNCE的核心思想在于样本$x_i$的正样本集合（${\mathcal{P}}_i$）和负样本集合（${\mathcal{N}}_i$）的构建。直觉上，在RGB流中很难“发现”的正样本往往可以在光流stream中“容易地”确定。例如，在静态相机设置下，特定动作（如高尔夫挥杆）的光流模式在不同实例之间可能非常相似，尽管在RGB表征中存在显著的背景变化（如图1所示）。即使使用不完全训练的光流网络，也可以发现这种相似性。这个观察使得两个模型，一个用于RGB，另一个用于光流，可以被协同训练，从启动阶段开始随着训练的进行逐渐增强两者的表征能力。
具体来说，我们通过从数据的另一个视图挖掘正样本对来协同训练模型。RGB表征$f_1(\cdot )$的更新是用多实例InfoNCE损失（包括我们在下面定义的正样本集合${\mathcal{P}}_i$中的一个或多个实际正样本的情况）：
$${\mathcal{L}}_1=-\mathbb{E}\left[\log \frac{{\sum }_{p\in {\mathcal{P}}_{1i}}\exp (z_{1i}\cdot z_p/\tau )}{{\sum }_{p\in {\mathcal{P}}_{1i}}\exp (z_{1i}\cdot z_p/\tau )+{\sum }_{n\in {\mathcal{N}}_{1i}}\exp (z_{1i}\cdot z_n/\tau )}\right]\text{\hspace{1em}(2)}$$其中分子定义为样本$x_{1i}$（在RGB视图中）与正样本集合之间的“相似性”之和，该正样本集是由与$x_{2i}$最相似的视频短片构建（光流视图中最相似的视频短片）：
P 1 i = { ψ ( x 1 i ; a ) , x 1 k ∣ k ∈ t o p K ( z 2 i ⋅ z 2 j ) , ∀ j ∈ [ 1 , N ] , a ∼ A } (3) \mathcal{P}_{1i}=\{\psi(x_{1i};a),x_{1k}|k\in\mathrm{topK}(z_{2i}·z_{2j}),\forall j\in[1,N],a\sim A\}\tag{3} P1i​={ψ(x1i​;a),x1k​∣k∈topK(z2i​⋅z2j​),∀j∈[1,N],a∼A}(3)$z_{2i}\cdot z_{2j}$表示光流视图中第$i$个和第$j$个视频之间的相似度，$\mathrm{topK}$操作是在所有可用的$N$个样本中选择$\mathrm{top}K$项并返回其索引。$K$是一个超参数，表示正样本挖掘的严格程度。样本$x_i$的负样本集合${\mathcal{N}}_{1i}$为正样本集合的补集，${\mathcal{N}}_{1i}=\overline{{\mathcal{P}}_{1i}}$。也就是说，正样本集合由光流特征空间中的前$K$个最近的neighbour加上视频短片自身的增强组成，负样本集合包含所有其它视频短片及其增强。
类似地，为了更新光流表征$f_2(\cdot )$，我们可以优化：
$${\mathcal{L}}_2=-\mathbb{E}\left[\log \frac{{\sum }_{p\in {\mathcal{P}}_{2i}}\exp (z_{2i}\cdot z_p/\tau )}{{\sum }_{p\in {\mathcal{P}}_{2i}}\exp (z_{2i}\cdot z_p/\tau )+{\sum }_{n\in {\mathcal{N}}_{2i}}\exp (z_{2i}\cdot z_n/\tau )}\right]\text{\hspace{1em}(4)}$$它是与公式2相同的目标函数，只是正样本集合现在是由RGB视图中的相似性排序构建的：
P 2 i = { ψ ( x 2 i ; a ) , x 2 k ∣ k ∈ t o p K ( z 1 i ⋅ z 1 j ) , ∀ j ∈ [ 1 , N ] , a ∼ A } (5) \mathcal{P}_{2i}=\{\psi(x_{2i};a),x_{2k}|k\in\mathrm{topK}(z_{1i}·z_{1j}),\forall j\in[1,N],a\sim A\}\tag{5} P2i​={ψ(x2i​;a),x2k​∣k∈topK(z1i​⋅z1j​),∀j∈[1,N],a∼A}(5)CoCLR算法分为初始化（initialization）和交替（alternation）两个阶段。
初始化。首先，使用InfoNCE独立训练两个不同视图的模型，即通过优化${\mathcal{L}}_{\mathrm{InfoNCE}}$训练RGB和Flow网络。
交替。使用${\mathcal{L}}_{\mathrm{InfoNCE}}$进行训练后，RGB和Flow网络都获得了远远强于随机初始化网络的表征。然后，协同训练过程如公式2和公式4所示，例如，为了优化${\mathcal{L}}_1$，我们使用Flow网络挖掘难正样本对；为了优化${\mathcal{L}}_2$，使用RGB网络挖掘难正样本对。这两种优化是交替进行的：每次先从另一个网络中挖掘出难正样本，然后独立地最小化网络的损失。随着联合优化的进行，以及表征变得更强，不同（且更难）的正样本被检索。
定义交替过程的关键超参数有：用于检索$K$个语义相关视频短片的$K$值，以及最小化每个损失函数的迭代次数（或epoch数），即交替的粒度。这些选择在第4.4节的消融中被探索，其中将看到选择$K=5$是最优的，并且更多的循环交替是有益的；这里的每次循环表示${\mathcal{L}}_1$和${\mathcal{L}}_2$的完全优化；也就是说，这种交替只发生在RGB或Flow网络收敛之后。
讨论。 首先，与我们之前使用InfoNCE进行视频自监督的工作DPC和MemDPC相比，所提出的CoCLR包含了从潜在更难的正样本中学习，例如来自同一类别的实例，而不是仅从同一实例的不同增强中学习；其次，CoCLR与UberNCE的oracle建议不同，因为CoCLR的正负样本集合中仍然可能包含“标签”噪声，即类别级的假正样本和假负样本。但实际上，CoCLR使用的多实例InfoNCE对噪声具有颇好的鲁棒性。最后，CoCLR与CMC和CVRL这两种仅使用实例级训练的同期方法有本质的区别，即它们是从同一数据样本中构造的正样本对。具体来说，CMC将正样本扩展为包含同一视频短片的不同视角，即RGB和flow，但没有在短片之间引入正样本；CVRL使用以视频短片为实例的InfoNCE对比学习。我们在表1中给出了InfoNCE和CMC的实验结果。

4 Experiments

本节首先介绍CoCLR训练的数据集（4.1节）和实现细节（4.2节）。在4.3节中，我们描述了用于评估自监督学习获得的表征的下游任务。所有的概念验证和消融研究都是在UCF101上进行的（4.4节），在Kinetics-400上进行了更大规模的训练（4.5节），以与其它SOTA方法进行比较。

4.1 Datasets

我们使用两个视频动作识别数据集进行自监督CoCLR训练：UCF101，包含13k个视频，涵盖101个人体动作（我们只使用来自训练集的视频）；和Kinetics-400（K400）仅从其训练集中获得的240k个视频片段。对于下游评估任务，我们在UCF101 split1、K400验证集以及HMDB51 split1上进行了测试，该数据集包含7k个视频，涵盖51个人体动作。

4.2 Implementation Details for CoCLR

我们选择S3D结构作为所有实验的特征提取器。在CoCLR训练过程中，我们附加一个非线性投射头，并将其移除后用于下游任务评估，如SimCLR所做。我们使用32帧的RGB（或flow）短片作为输入，在30 fps的速度下，这大致覆盖了1秒。视频短片的空间分辨率为128×128像素。对于数据增强，我们应用了随机crop、水平翻转、高斯模糊和颜色抖动，都是短片级（clip-wise）一致的。我们还应用随机时间裁剪来利用时间维度的自然变化，即输入的视频短片被裁剪为源视频的随机时间戳。光流的计算采用无监督的TV-L1算法，预处理过程与K400原文相同。具体来说，双通道的动作场与第三个零值通道堆叠，超过20个像素的大动作被删节，值最终从$[-20,20]$投射到$[0,255]$，然后压缩为jpeg。
在初始化阶段，我们使用InfoNCE对RGB和Flow网络进行了300个epoch的训练，其中一个epoch意味着从训练集中的每个视频中采样了一个视频短片，即所看到的实例总数与训练集中的视频数量相等。我们采用动量更新历史队列来高速缓存大量的特征，就和MoCo中一样。在交替阶段，在UCF101上模型训练两个循环，每个循环包含200个epoch，即RGB和Flow网络分别训练100个epoch，并相互进行难正样本挖掘；在K400上，模型只训练了一个循环100个epoch，即RGB和Flow网络各训练50个epoch，但我们预计更多的训练循环是有益的。对于优化，我们使用Adam，学习率为$10^{-3}$权重衰减为$10^{-5}$。当验证损失稳定时，学习率衰减$1/10$倍。各个实验在4个GPU上进行训练，每个GPU的batch size为32个样本。

4.3 Downstream tasks for representation evaluation

动作分类。 在该协议中，我们在两个设置上进行评估：①linear probe：整个特征编码器被冻结，只有单个线性层使用交叉熵损失训练；②finetune：整个特征编码器和线性层端到端地使用交叉熵损失微调，即CoCLR训练得到的表征只为网络提供初始化。
在训练阶段，我们应用了与4.2节中提到的预训练阶段相同的数据增强，除了高斯模糊。在推理阶段，我们遵循与我们之前的工作相同的步骤：对于每个视频，我们在空间上应用10个裁剪（中心裁剪加上四个角，使用水平翻转），在时间上使用移动窗口来取短片（半时间重叠），然后对预测概率进行平均。
动作检索。 在该协议中，提取到的特征直接用于最近邻（nearest-neighbour，NN）检索，不允许进一步的训练。我们遵循常见的做法，使用测试集视频短片从训练集中查询$k$-NNs。我们报告Recall at $k$（R@$k$），也就是说，如果前$k$个最近邻包含一个相同类别的视频，则计数一个正确的检索。

4.4 Model comparisons on UCF101

本节展示了从InfoNCE到UberNCE再到CoCLR的演变过程，并监测了动作分类的top1准确率和检索性能。在本节中，使用同样的数据集UCF101 split # 1进行自监督训练和下游评估，我们主要关注linear probe&retrieval作为表征质量的主要度量，因为它们的评估速度快。对于所有的自监督预训练，我们保持设置相同，例如训练epochs，只改变挖掘正样本对的过程。
**Linear probe & retrieval。**这里的讨论将集中在RGB网络上，因为这个网络易于使用（无需光流计算）并且提供了快的推理速度，但是CoCLR和CMC的训练都是用RGB和Flow完成的。如表1所示，可以观察到三个现象：首先，有监督对比方法UberNCE优于InfoNCE基线，在linear probe（78.0 vs 46.8）和retrieval（71.6 vs 33.1）上有显著差距，这揭示了基于实例的自监督学习的次优性。其次，协同训练方案（CoCLR）显示了其有效性，比InfoNCE和CMC基线从46.8和55.0大幅提升至70.2，接近UberNCE的结果（78.0）。最后，结合RGB和Flow网络的logits带来了进一步的好处。我们猜想，一个更现代的RGB网络，如SlowFast，能够自然地捕获更多的动作信息，将进一步缩小差距。

端到端的微调。 在该协议中，所有模型（RGB网络）的表现都很好，不同训练方案之间的差距是微不足道的（77.0~81.4）。这是预料之中的，因为同样的数据集，数据视图和结构已经被用于自监督学习、微调或从头开始训练。在本文中，我们更感兴趣的场景是在大规模数据集上进行预训练，例如Kinetics，特征可迁移性在linear probe上进行评估，并在另一个小数据集上进行微调，如4.5节所示。
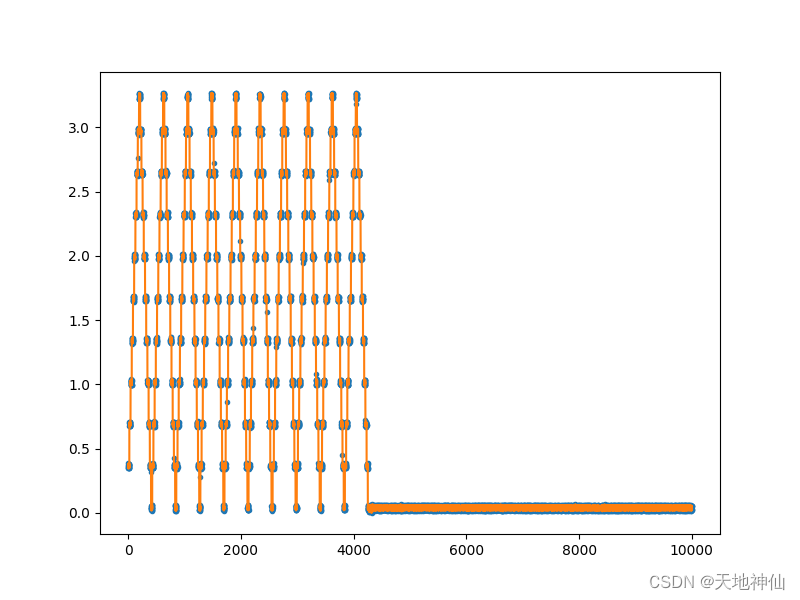
为了更好地理解协同训练对挖掘难正样本的有效性，在图2中，我们通过测量R@1来检测交替过程。需要注意的是，标签信息仅用于绘制此曲线，在自监督训练时并不使用。x轴表示训练阶段，由InfoNCE表征初始化，然后交替训练${\mathcal{L}}_1$和${\mathcal{L}}_2$两个循环，如3.2节所述。虚线表示某个网络是固定的，实线表示该表征正在被优化。随着训练的进行，RGB和Flow模型的表征质量都随着更多的协同训练循环而提高，表现为R@1性能的提高，这表明具有相同类别的视频短片确实在嵌入空间（embedding space）中被拉（pull）到了一起。

消融。 我们还对CoCLR超参数的其它选择进行了实验，结果报告在表1的底部。就公式3和公式5中挖掘的样本数量而言，$K=5$是最优设置，即使用Top5最相似的样本训练目标表征。其它值，$K=1$和$K=50$略差。就交替粒度而言，我们与同时优化两个表征的极端情况进行了比较（$\mathrm{CoCL}{\mathrm{R}}_{\mathrm{K}=5};\mathrm{sim}$），同样，比训练一个网络而另一个网络固定来“充当”oracle的性能略差。我们猜测同步优化的性能较差是因为网络的权重更新过快，类似的现象在其它工作中也观察到过，我们留待以后工作进一步研究。

4.5 Comparison with the state-of-the-art

在本节中，我们将CoCLR与之前的自监督动作分类方法进行比较。具体来说，我们提供了两种设置下的CoCLR结果，即在UCF101上以$K=5$训练2个循环；和在K400上以$K=5$仅1次循环。值得注意的是，关于视频自监督学习已经有了丰富的文献，在表2中我们只列出了最近在同一基准上评估的一些方法，并尝试在结构、训练数据、分辨率等方面尽可能公平地与它们进行比较（尽管仍存在变化）。
下面我们将与使用了：①相同训练集上的纯视觉信息；②更大训练集上的纯视觉信息；③多模态信息来训练的方法进行比较。
使用相同训练集的纯视觉信息（微调）。 当比较UCF101上只训练（自监督并下游微调）的模型时，例如OPN和VCOP，提出的CoCLR（RGB网络）在UCF101上获得了81.4的Top1精度，HMDB上获得了52.1的Top1精度，显著优于之前的方法。在K400上，最近的方法包括3D-RotNet、ST-Puzzle、DPC、MemDPC、XDC、GDT和SpeedNet。再次，CoCLR（RGB网络）超越了其它的自监督方法，在UCF101上达到了87.9，在HMDB上达到了54.6，并且双流CoCLR会带来进一步的好处（在UCF101上90.6，在HMDB上62.9）。我们注意到CoCLR的性能略逊于CVRL，我们猜测是由于CVRL使用了更深的结构（23层vs.49层），包含了更多的参数（7.9M vs. 33.1M），更大的分辨率（128 vs. 224），更强的颜色抖动，以及更多的epoch（400 epochs vs. 800 epochs）。这也表明CoCLR还有进一步改进的空间，从使用InfoNCE训练的更好的初始化开始。
使用更大训练集的纯视觉信息（微调）。 虽然只使用了视觉信息，但有些方法使用了更大的训练集，例如CBT和DynamoNet。CoCLR仍然优于所有这些方法，显示了其非凡的训练效率，因为它可以用更少的数据学习更好的表征。
多模态信息（微调）。 这些都是利用视觉信息与文本或音频关联的方法。这些方法通常在更大规模的数据集上进行训练，例如在AudioSet（比K400大8倍）上训练的AVTS，以及在IG65M（比K400大273倍）上训练的XDC，用于音频-视觉关联；MIL-NCE在解说指导的视频（比K400大195倍）上进行视觉-文本关联训练；ELO在200万个视频（比K400大104倍）上用7种不同的损失进行训练。尽管有这些相当大的数据集，以及来自其它模态的信息，我们最好的纯视觉CoCLR（双流网络）仍然与它们相当。值得注意的是，我们的CoCLR方法也不局限于纯视觉的自监督学习，并且非常适合从音频或文本中挖掘难正样本。

Linear probe。 如表2上半部分所示，CoCLR在自监督训练的数据量相同或仅占极小比例的情况下，显著优于MemDPC和CBT，并与训练数据量多了几个数量级的MIL-NCE、XDC和ELO相当。
视频检索。 除了动作分类基准，我们还评估了CoCLR在视频检索上的性能，如4.3节所述。目标是测试查询短片实例与其最近邻是否属于同一语义类别。如表3所示，在两个基准数据集上，InfoNCE基线模型都以显著的优势超过了之前的所有方法。我们的CoCLR模型远远超过了InfoNCE模型。

视频检索的定性结果。 图3是使用CoCLR embedding从UCF101训练集中可视化的一个查询视频短片及其Top3最近邻。可以看出，CoCLR学习到的表征具有检索相同语义类别视频的能力。

5 Conclusion

我们已经证明，视频的互补视图可以用于弥补同一类别的RGB视频短片实例之间的差距，并且使用该视图生成正样本训练集可以显著提高InfoNCE实例训练的性能用于视频表征。虽然我们没有在本文中展示，但我们猜想从音频中显式挖掘也可以提供类似于光流的作用。例如，吉他的声音可以将具有非常不同的视觉外观的视频短片关联在一起，即使音频网络相对地没有训练。这一观察部分地解释了音频-视觉自监督学习的成功，其中这样的关联是隐式发生的。同样且更明显的是，在视觉-文本学习中，文本提供了实例之间的桥梁，例如视频中描述其视觉内容的解说。我们预期，CoCLR中显式正样本挖掘的成功将导致应用到其它数据，如图像、其它模态和任务，在这些数据中可以提取其它视图以提供补充信息，并且也可以用到其它的学习方法，如BYOL。