目录
1. 二进制数、八进制数、十六进制数转换为十进制数
2. 十进制数转换为二进制数、八进制数、十六进制数
3. 二进制数和十六进制数的相互转换
4. 使用电脑计算器进行进制转换
1. 二进制数、八进制数、十六进制数转换为十进制数
十进制数的每一位都是10的指数幂。如,
1998 = 1×10^3 + 9×10^2 + 9×10^1 + 8×10^0
将这个思路应用于二进制数、八进制数、十六进制数,就能将这些数转换为十进制数。
二进制数101转换为十进制数:
101 = 1×2^2 + 0×2^1 + 1×2^0 = 5
八进制数123转换为十进制数:
123 = 1×8^2 + 2×8^1 + 3×8^0 = 83
十六进制数1FD转换为十进制数:
1FD = 1×16^2 + 15×16^1 + 13×16^0 = 509
2. 十进制数转换为二进制数、八进制数、十六进制数

将这个思路应用于二进制数、八进制数、十六进制数,就能将十进制数转换为二进制数、八进制数、十六进制数。
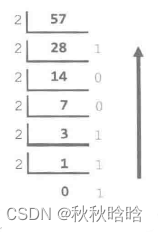
十进制数57转换为二进制数:
111001
十进制数57转换为八进制数:
71
十进制数57转换为十六进制数:
39
给定一个十进制数M(32位整数),以及需要转换的进制数N(2≤N≤16)。将十进制数M转化为N进制数:
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;
int main() {
string s;
string table = "0123456789ABCDEF";//表示映射关系
int m, n;
while (cin >> m >> n)
{
if (m == 0)
{
cout << 0 <<endl;
}
bool flag = false;//默认情况下m是正数
if (m < 0)
{
m = -m;//如果m是负数,取相反数,变成正数
flag = true;//flag=true表示m本来是负数
}
while (m != 0)
{
s += table[m%n];//将余数拼接到字符串
m /= n;
}
if (flag == true)
{
s += "-";//如果m本来是负数,加上负号
}
reverse(s.begin(), s.end());//倒置字符串
cout << s <<endl;
}
}3. 二进制数和十六进制数的相互转换
4位二进制数和1位十六进制数是相互对应的(即4位的二进制数0000~1111,就是1位的十六进制数0~F)。
| 二进制数 | 十六进制数 |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
二进制数0111101010011100转换为十六进制数:
0111 1010 1001 1100
7 A 9 C
十六进制数8AF7转换为二进制数:
8 A F 7
1000 1010 1111 0111
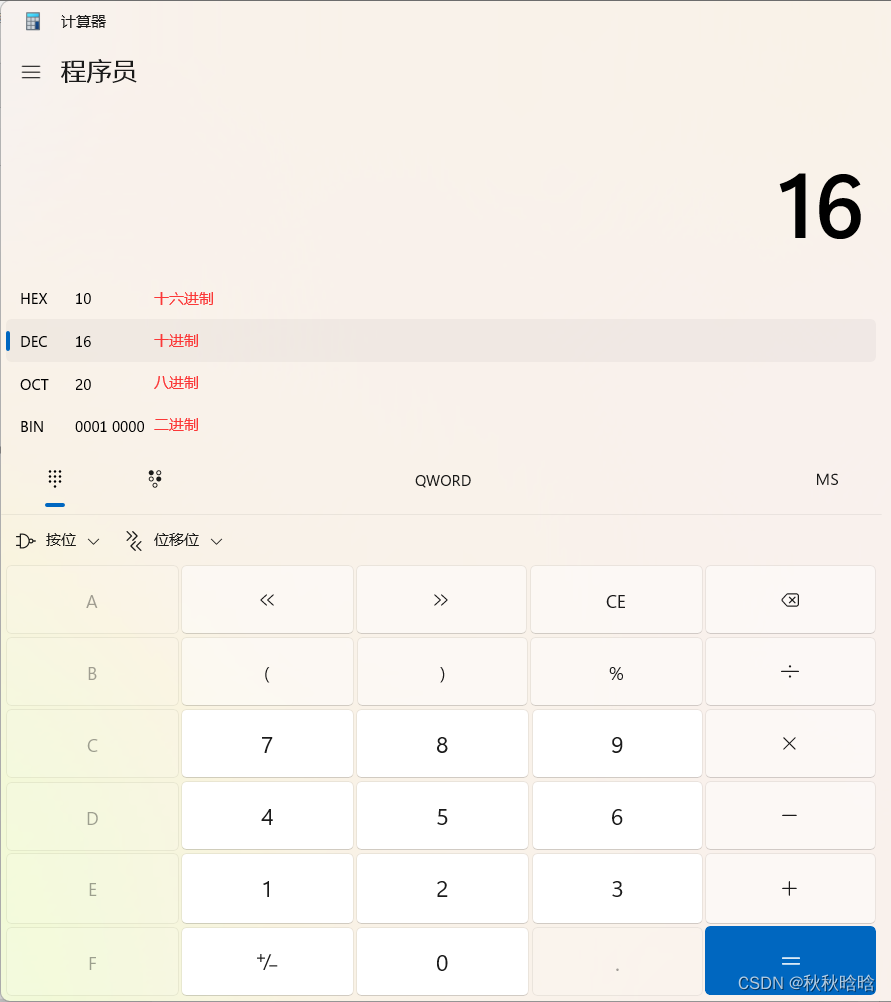
4. 使用电脑计算器进行进制转换
将计算器切换为程序员选项:
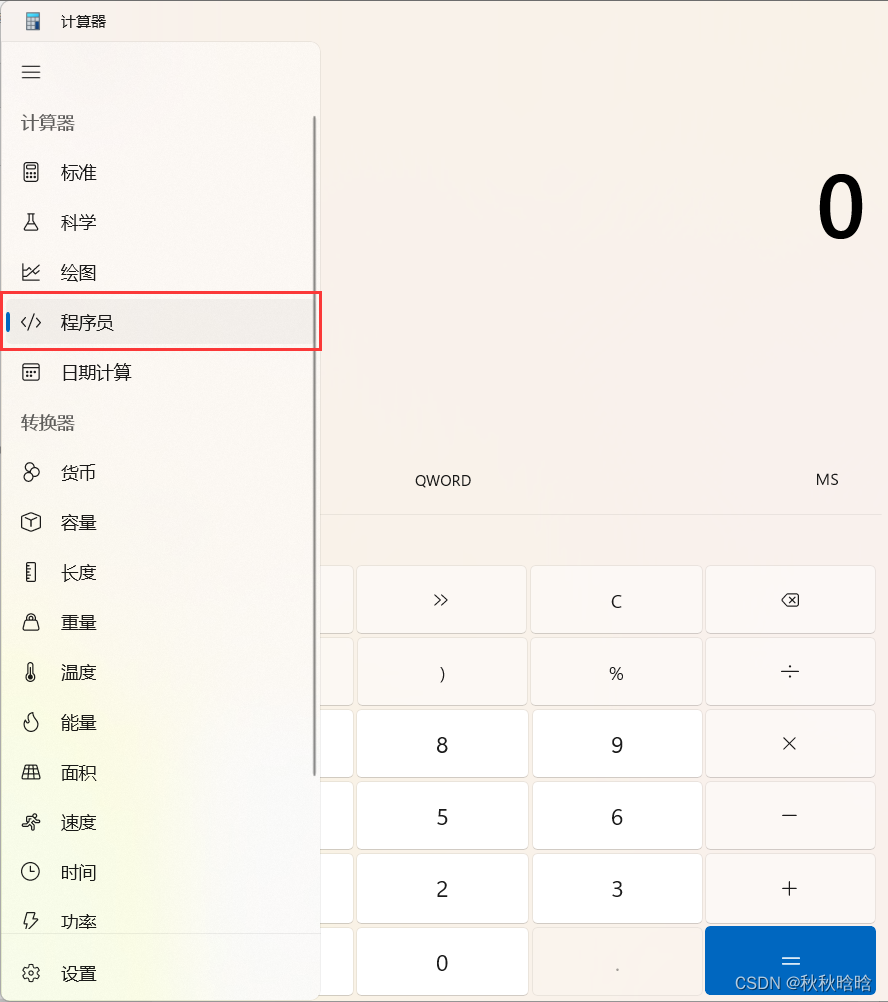
将十进制数16转换为二进制数、八进制数、十六进制数: