一、非支配排序的鲸鱼优化算法
非支配排序的鲸鱼优化算法(Non-Dominated Sorting Whale Optimization Algorithm,NSWOA)由Pradeep Jangir和 Narottam Jangir于2017年提出。


NSWOA算法流程如下:

二、RBF神经网络
1988年,Broomhead和Lowc根据生物神经元具有局部响应这一特点,将RBF引入神经网络设计中,产生了RBF(Radical Basis Function)。1989年,Jackson论证了RBF神经网络对非线性连续函数的一致逼近性能。
RBF的基本思想是:用RBF作为隐单元的“基”构成隐藏层空间,隐含层对输入矢量进行变换,将低维的模式输入数据变换到高维空间内,使得在低维空间内的线性不可分的问题在高维空间内线性可分。
RBF神经网络结构简单、训练简洁而且学习收敛速度快,能够逼近任意非线性函数,因此已被广泛应用于时间序列分析、模式识别、非线性控制和图形处理等领域。
RBF神经网络学习算法需要优化的参数有3个:基函数的中心、方差以及隐含层到输出层的权值。
基于高斯核的RBF神经网络拓扑结构:
第一层输入层:由信号源节点构成,仅起到数据信息的传递作用,对输入信息不做任何变换
第二层隐含层:节点数视需要而定。隐含层神经元核函数(作用函数)是高斯函数,对输入信息进行空间映射的变换。
第三层输出层,对输入模式做出响应。输出层神经元的作用函数为线性函数,对隐含层神经元输出的信息进行线性加权后输出,作为整个神经网络的输出结果。

三、非支配排序的鲸鱼优化算法NSWOA优化RBF神经网络
非支配排序的鲸鱼优化算法NSWOA中每个个体由基函数的中心、方差以及隐含层到输出层的权值构成,两个目标函数为样本真实值与预测值的均方误差(MSE)。训练数据集为6个输入,2个输出,共300个样例。构建结构为6-10-2的RBF神经网络,其中隐藏层神经元数目可以修改。
部分样例如下:(前6列为输入,后2列为输出)
0.713579996594884 0.973568402691768 0.0824448224264940 0.585264837959374 0.531414173953683 0.856365367019255 1.32743899297506 2.41519860767040
0.218557762664222 0.888419469848967 0.939959005198331 0.711424938174573 0.449737107676159 0.812247345729087 1.60825387553871 2.41209175375263
0.210845792953702 0.291848474251125 0.817985975534208 0.0224069835293927 0.642499428553517 0.464226773276162 1.67133119704143 0.778482231056679
0.138925583640368 0.150529446517112 0.281251506709573 0.0289283211915973 0.348706368098486 0.903657252375479 0.768883458448428 1.08311502008419
0.679015819172490 0.210504001944847 0.506998736255627 0.0143607498566152 0.892442419026897 0.566823504951400 2.07845697445501 0.791688256752862
0.0520848926590219 0.154913533271986 0.0557509606785225 0.916497166251544 0.0697163732653581 0.591405090114828 0.177552226602902 1.66281578963836
0.0810950135454228 0.269334511629595 0.754531447868779 0.139215440452895 0.459460537278416 0.0419227996933343 1.29508699869262 0.450472751775824
0.927299917256754 0.741521161159710 0.747005122998480 0.112919143211011 0.467921048750087 0.743709711696814 2.14222608900532 1.59815001606753
0.928165532557930 0.472203377881395 0.683036636925367 0.206504589377546 0.903236727308788 0.729565383108516 2.51443889679209 1.40827335036746
0.191494299273308 0.491535033231124 0.967782075039601 0.878017316272317 0.304171048995970 0.182382593579523 1.46344742330888 1.55193494308296
0.518113080400652 0.362748260135582 0.209806887695183 0.956451054998756 0.510052514763925 0.790610340906869 1.23797248285976 2.10980965604121
0.830713356252473 0.751748214027656 0.316186995843160 0.617428331451750 0.475194292178331 0.561777637615592 1.62209464427396 1.93095418309500
0.142256115752167 0.248628311738998 0.464354034178816 0.0459195257000721 0.382991165602749 0.430631218266837 0.989601315533732 0.725179055705907
0.756177912918820 0.394826363724776 0.714308626604904 0.792136982678444 0.316946044903704 0.814129928334899 1.78743258442743 2.00109327473812
0.636267440609688 0.696754012036900 0.948325910043440 0.565577362012063 0.755877881232562 0.195634834495328 2.34047123188569 1.45796620854429
0.0894354528968515 0.774878326539918 0.761255673320979 0.450222594452581 0.119946316991966 0.837217733177432 0.970637443209796 2.06231865416993
0.490846637046064 0.238559840946110 0.880383966782141 0.849756780444547 0.364265992607895 0.159017465755099 1.73549659643610 1.24733408714576
0.562256680322090 0.421278711197472 0.0548573856716194 0.103518820683544 0.196625841528628 0.534104471459144 0.813739907522337 1.05890200334016
0.359507176414332 0.131440307233889 0.487121117853134 0.558834800863296 0.927027286166390 0.213694822584527 1.77365558043386 0.903969930681711
0.187063542906367 0.612424846727939 0.0553117989895839 0.212760776106613 0.642309868487962 0.896181269095994 0.884685210383912 1.72136689193055
0.786500401198605 0.635675576516305 0.777686342722035 0.424039116519014 0.391810970884959 0.889827824797412 1.95599771480560 1.94954251783273
0.510093025740105 0.180135530430196 0.802368302424647 0.332104156050016 0.379416525315520 0.792981620086756 1.69187785348027 1.30522130656697
0.163936208611282 0.397650330010963 0.406461343190970 0.787572874688299 0.856142621359846 0.557263065211912 1.42654017316210 1.74248626991117
0.222944554515944 0.172888824306559 0.131734775822207 0.113721858923443 0.281167201030943 0.366425511609739 0.635846531369094 0.653036194839741
0.994176240512781 0.309652781208750 0.430164650695471 0.334698769797657 0.935287723130266 0.243596965312906 2.35962861433852 0.887948516319314
0.612502638977732 0.280104345526887 0.0320728504877658 0.637477847090346 0.562511849201201 0.937730332243288 1.20708733866670 1.85531252486052
0.0445534978647620 0.839876814539396 0.818964442816881 0.0237621903267523 0.00971624164550933 0.966216417652830 0.873234182327152 1.82985542251898
0.687768579812269 0.498923080114782 0.784427811219562 0.131568810381094 0.697482023708840 0.0909859966689093 2.16967841474067 0.721477887164785
0.696277135120957 0.252109542567679 0.379538502367650 0.296769112885393 0.331565505654575 0.994905858431417 1.40738114314318 1.54378451388449
0.913720809929107 0.683353086105831 0.202985701891935 0.451210891843151 0.508794036450449 0.270392101042156 1.62550054827149 1.40495607899114
部分代码如下:(完整代码可以私聊博主或添加博主微信)
close all;
clear ;
clc;
%% NSWOA优化RBF 决策变量为RBF待优化参数,两个目标函数分别为真实值和预测值的均方误差
global inputnum hiddennum outputnum TrainNum
inputnum=6;%神经网络输入层神经元个数(输入样本维度)
hiddennum=10;%神经网络隐藏层神经元个数(可以自己修改)
outputnum=2;%神经网络输出层神经元个数(输出样本维度)
TrainNum=300;%训练集数目
TestProblem=1;%
MultiObj = GetFunInfo(TestProblem);
MultiObjFnc=MultiObj.name;%问题名
% Parameters
params.Np = 100; % Population size
params.Nr = 200; % Repository size
params.maxgen =5000; % Maximum number of generations
[x,f] = NSWOA(params,MultiObj);
% x是PS
% f是PF
%% 计算算法的评价指标Spacing,Spacing越小说明解集分布越均匀
ResultData=Spacing(f);%计算的Spacing
%% 找出两个目标的均方误差和最小的个体作为最优解bestX
[~,idx]=min(sum(f,2));
bestX=x(idx,:);
save x x %保存PS
save f f %保存PF
save bestX bestX %保存最优解bestX
Predata;%求解结果展示
四、预测结果

找出两个目标的均方误差和最小的个体作为最优解bestX,在最优解下预测结果:
在第一个目标上的真实值与预测值:

在第二个目标上的真实值与预测值:
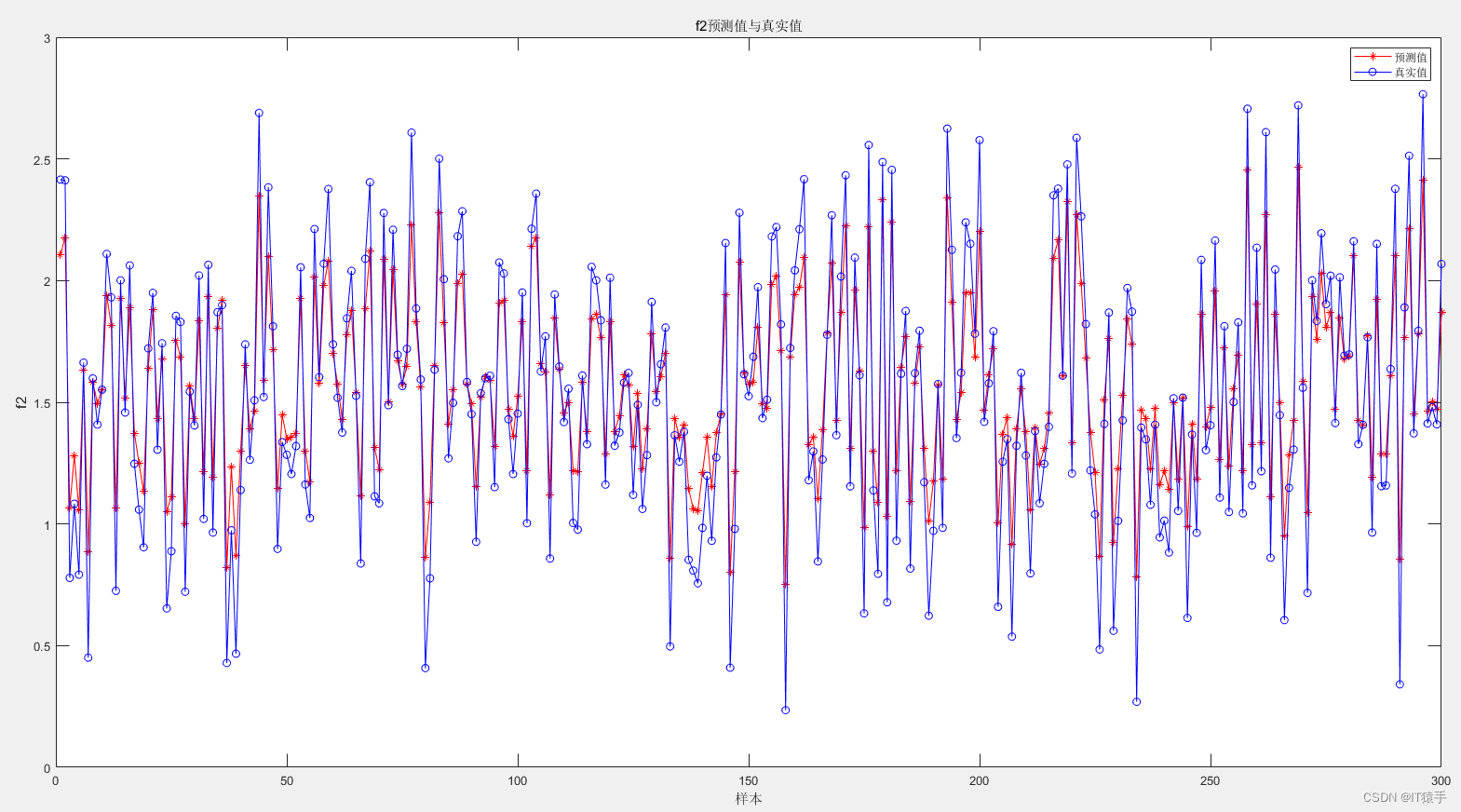
两个目标的真实值与预测值的误差MAE:




![[附源码]计算机毕业设计JAVAjsp心理测评系统](https://img-blog.csdnimg.cn/cb033dfc706b44f6954173a3b53694e2.png)