⭐前言⭐
※※※大家好!我是同学〖森〗,一名计算机爱好者,今天让我们进入复习模式。若有错误,请多多指教。更多有趣的代码请移步Gitee
👍 点赞 ⭐ 收藏 📝留言 都是我创作的最大的动力!
题目
704. 二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例1:
1| 输入: nums = [-1,0,3,5,9,12], target = 9
2| 输出: 4
3| 解释: 9在数组 nums 中,并且下标位置为 4
示例2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示:
- 你可以假设 nums 中的所有元素是不重复的。
- n 将在 [1, 10000]之间。
- nums 的每个元素都将在 [-9999, 9999]之间。
思路
题目分析:
- 从数组中查询元素,存在返回下标,不存在返回-1;
- 所有元素都是不重复的,不重复的升序数组
注: 如果是有重复元素的数组,使用二分查找返回的下表可能不唯一;- n的范围 [1, 10000] 和 nums[ i ] 的范围 [ -9999, 9999] 可以用 int 类型;
二分查找的思想
- 确定区间 left,right
- 用中间的元素与目标值 target 比较;
- 如果中间元素大于target的值,由于数组升序,中间元素向右的元素都大于 target,全部排除;
- 如果中间元素小于target的值,由于数组升序,中间元素向左的元素都小于 target,全部排除;
- 中间元素等于target, 返回中间元素的下标;
易错点
- 不确定区间的范围,[left,right] 和 [left,right)对于判断是 while( left < right) 和 while( left <=right)、right = mid 还是 right = mid + 1 至关重要;
接下来分别实现左闭右闭 [left, right] 和 左闭右开 [ left, right) 两种 区间分别求解
解法一 左闭右开
查询区间 [left, right)
控制条件
- 循环条件:while (left < right)
注: 这里是 小于,而不是 小于等于 因为 left == right 时 查询区间内没有元素了;- if(nums[mid] > target) right = mid; 因为nums[mid] > target , mid下标后面的元素都大于target,全部排除,因为区间是左闭右开,所以right = mid; 正好取不到mid; 如果不小心赋值成right = mid - 1,就漏掉了一个元素
- if(nums[mid] < target) left = mid + 1; 因为 查询区间左边可以取到,mid 检查过了,从mid + 1开始遍历 所以 left = mid + 1;
例:在数组:-1,0,3,5,9,12 中查询 元素 0
第一步:初始化 left 和 right
left = 0;
right = nums.length;
// 循环条件
while(left < right){
}
查询区间是[left, right) 第一步初始化如下

第二步:计算mid的值
left = 0;
right = nums.length;
// 循环条件
while(left < right){
// 防止溢出, 等同于(left + right) / 2
int mid = left + (right - left) / 2;
}
第一次计算mid
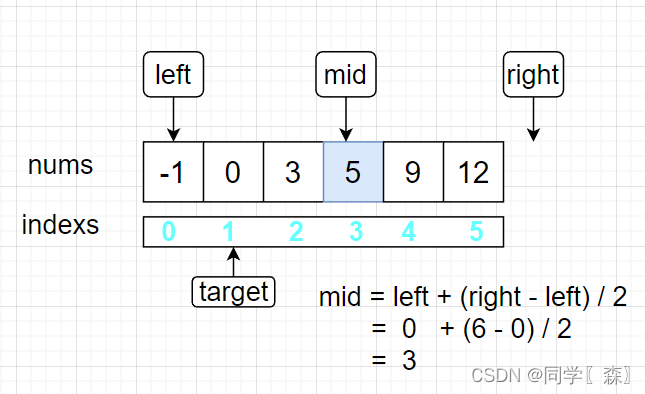
第三步:比较nums[mid] 和 target
left = 0;
right = nums.length;
// 循环条件
while(left < right){
// 防止溢出, 等同于(left + right) / 2
int mid = left + (right - left) / 2;
if(nums[mid] > target) {
// target 在左区间[left mid)
right = mid;
} else if (nums[mid] < target) {
// target 在右区间[mid + 1, right)
left = mid + 1;
} else { // nums[mid] == target
return mid; // 在数组中找到target, 直接返回下标
}
}
return -1; // 没有找目标值
比较nums[mid] 和 target的大小, nums[mid] = 5 > target = 0 right = mid
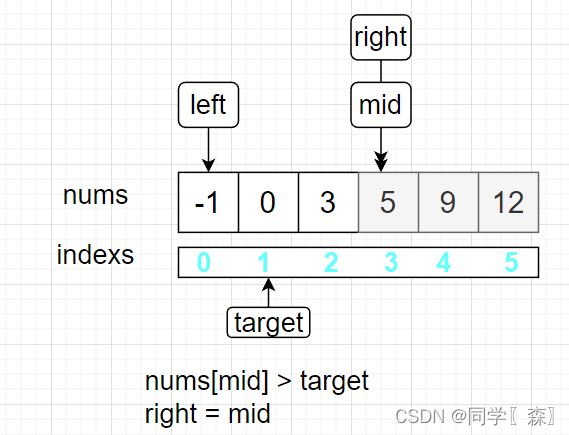
left < right ; 0 < 3 进入循环
- mid = left + (right - left) / 2 = 1
第二次计算mid
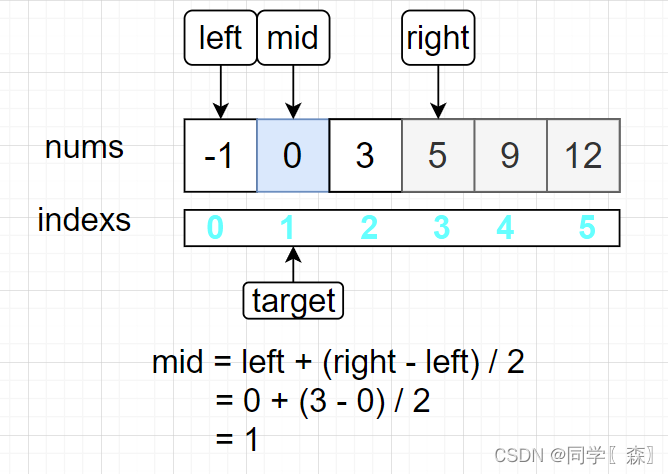
比较nums[mid] 和 target的大小, nums[mid] = 0 等于 target = 0
成功找到 target 返回 1;
完整代码
class Solution {
public int search(int[] nums, int target) {
int left = 0;
int right = nums.length;
// 循环条件
while(left < right){
// 防止溢出, 等同于(left + right) / 2
int mid = left + (right - left) / 2;
if(nums[mid] > target) {
// target 在左区间[left mid)
right = mid;
} else if (nums[mid] < target) {
// target 在右区间[mid + 1, right)
left = mid + 1;
} else { // nums[mid] == target
return mid; // 在数组中找到target, 直接返回下标
}
}
return -1; // 没有找目标值
}
}
运行结果:
错误演示
正确代码:while(left < right)
错误代码:while(left <= right)
例:在数组:-1,0,3,5,9,12 中查询 元素 7
完整代码
class Solution {
public int search(int[] nums, int target) {
int left = 0;
int right = nums.length;
// 循环条件
while(left <= right){
// 防止溢出, 等同于(left + right) / 2
int mid = left + (right - left) / 2;
if(nums[mid] > target) {
// target 在左区间[left mid)
right = mid;
} else if (nums[mid] < target) {
// target 在右区间[mid + 1, right)
left = mid + 1;
} else { // nums[mid] == target
return mid; // 在数组中找到target, 直接返回下标
}
}
return -1; // 没有找目标值
}
}
初始化:left = 0; right = arr.length;

mid = left + (right - left) / 2; mid = 3
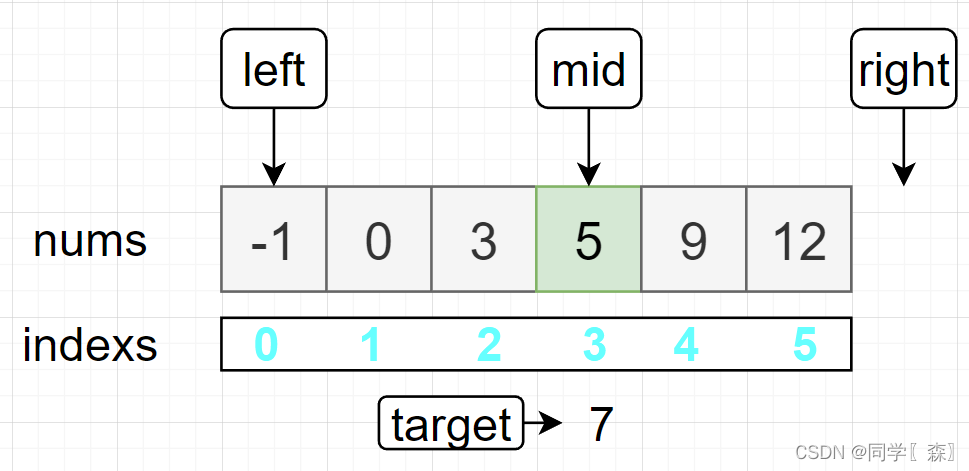
比较nums[mid] 和 target 大小 5 < 7 left = mid + 1 = 4;
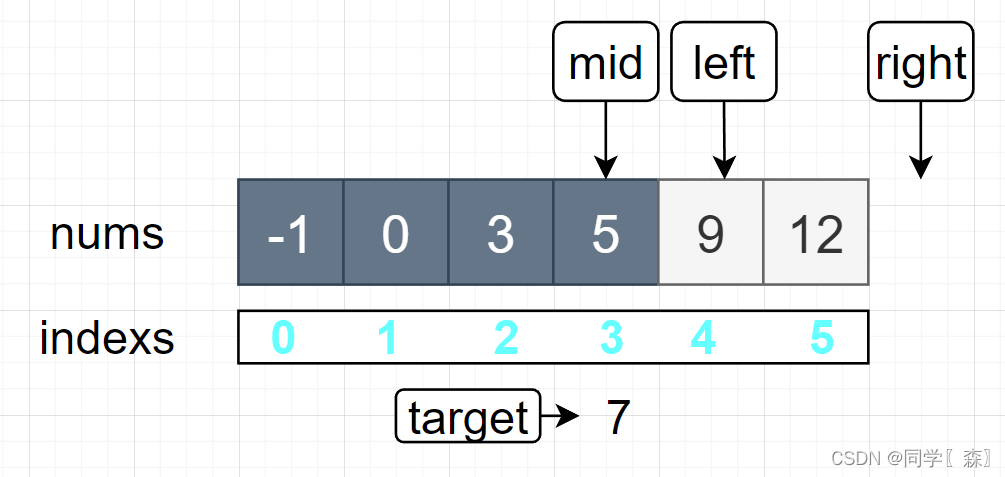
left <= right 4 < 6进入循环 mid = mid = left + (right - left) / 2; mid = 5

比较nums[mid] 和 target 大小 12 > 7 right = mid = 5
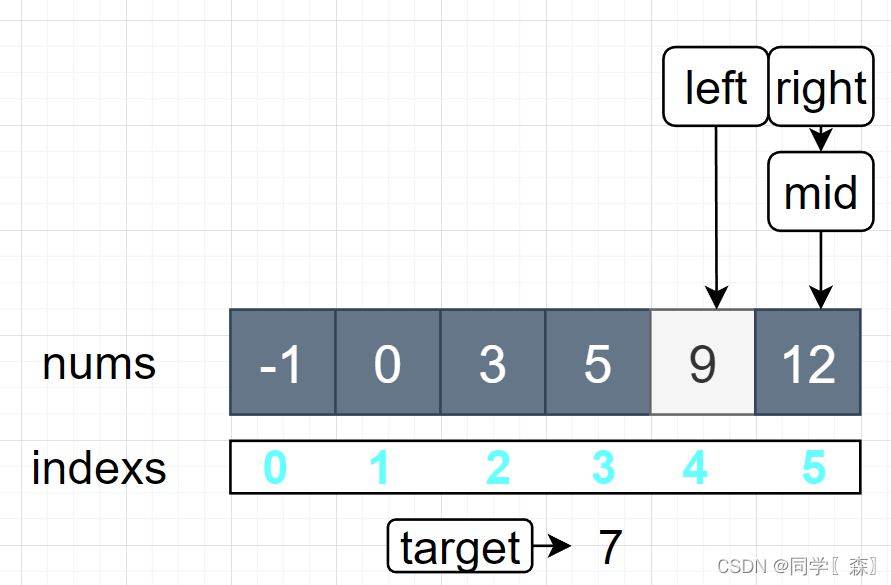
left <= right 4 < 5 进入循环 mid = left + (right - left) / 2; mid = 4
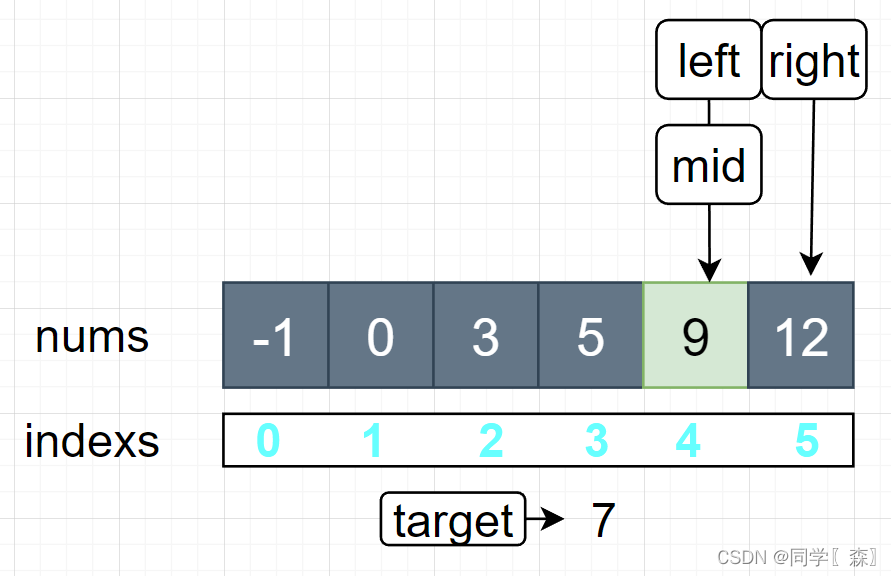
比较nums[mid] 和 target 大小 9 > 7 right = mid = 4

left <= right 4 = 4 进入循环, mid = left + (right - left) / 2; mid = 4;
比较nums[mid] 和 target 大小 9 > 7 right = mid = 4 程序进入了死循环;
解法二 左闭右闭
查询区间 [left, right]
控制条件
- 循环条件:while (left <= right) 要使用 <= ,因为left == right是有意义的,所以使用 <=
- if(nums[mid] > target) right = mid - 1; 因为当前这个nums[middle]一定不是target,那么接下来要查找的左区间结束下标位置就是 middle - 1
- if(nums[mid] < target) left = mid + 1;
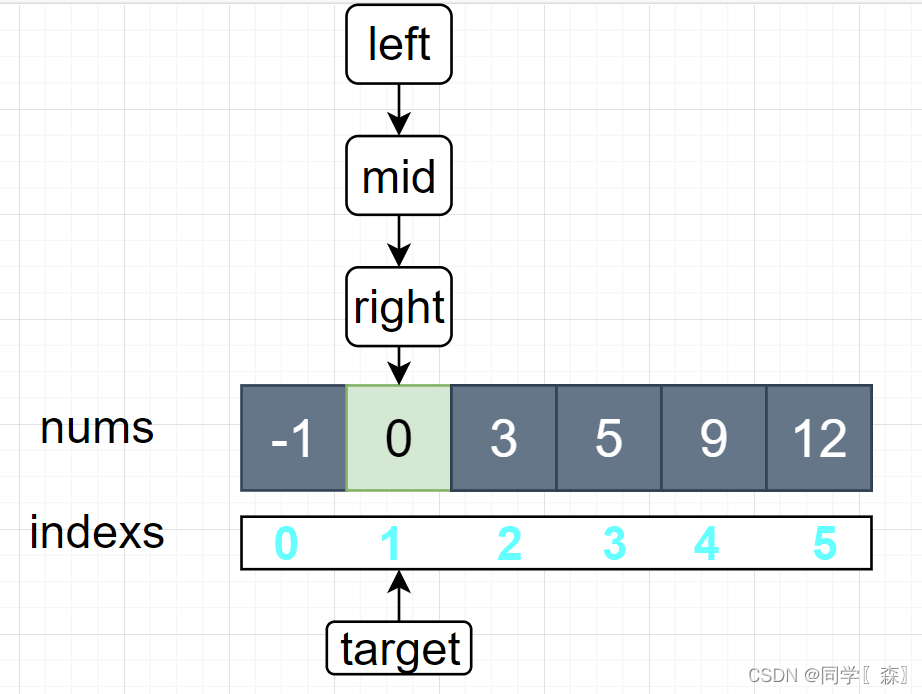
例:在数组:-1,0,3,5,9,12 中查询 元素 0
第一步初始化 left 和 right
left = 0;
right = nums.length - 1;
// 循环条件
while( left <= right) {
}
left right 初始化

第二步: 计算mid值
left = 0;
right = nums.length - 1;
// 循环条件
while( left <= right) {
int mid = left + (right - left) / 2;
}
mid = left + (right - left) / 2; mid = 0 + (5 - 0) / 2 = 2

第三步:比较nums[mid] 和target
left = 0;
right = nums.length;
// 循环条件
while(left <= right){
// 防止溢出, 等同于(left + right) / 2
int mid = left + (right - left) / 2;
if(nums[mid] > target) {
// target 在左区间[left mid - 1]
right = mid - 1;
} else if (nums[mid] < target) {
// target 在右区间[mid + 1, right]
left = mid + 1;
} else { // nums[mid] == target
return mid; // 在数组中找到target, 直接返回下标
}
}
return -1; // 没有找目标值
nums[ mid ] = 3 > target = 0 ; right = mid - 1 = 1
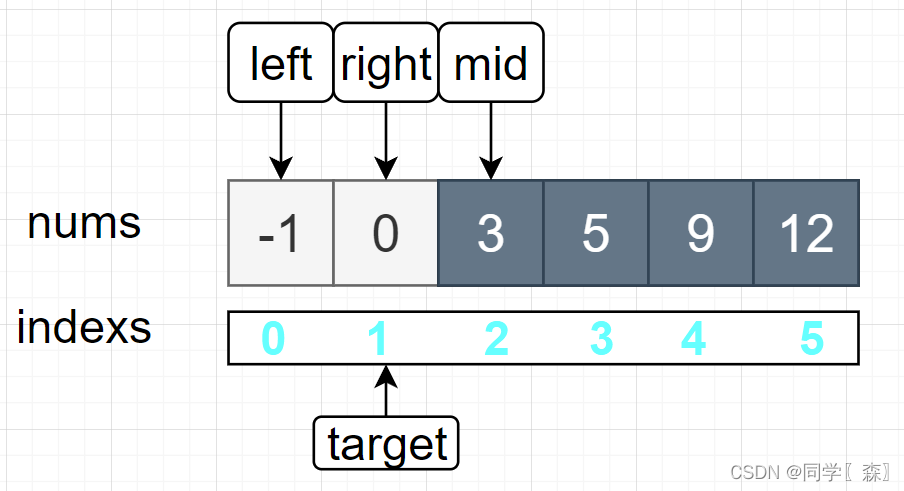
left = 0 , right = 1; 0 <= 1 进入循环; mid = left + (right - left) / 2; mid = 0;
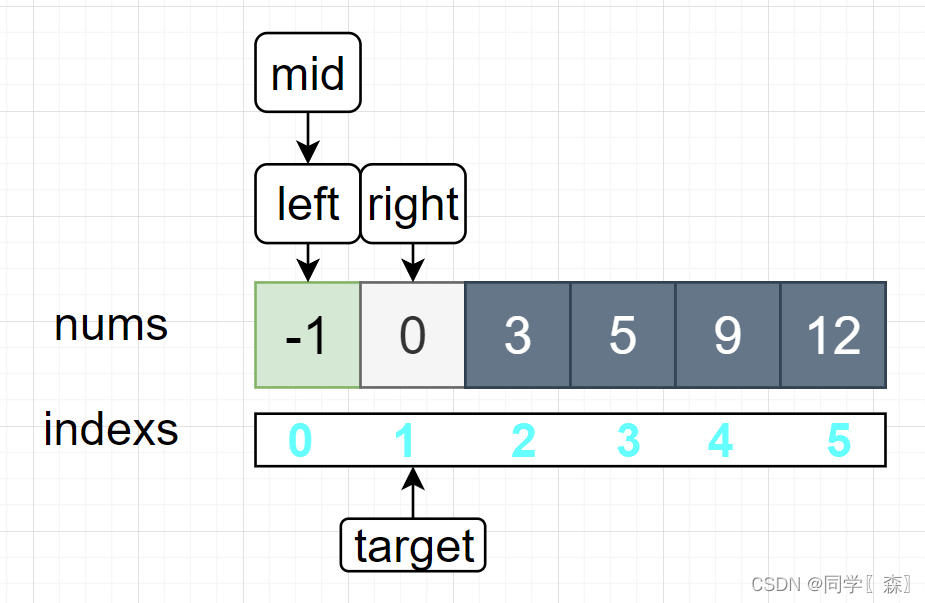
nums[ mid ] = -1 < target = 0 ; left = mid + 1 = 1

left = 1 , right = 1; 1 <= 1 进入循环; mid = left + (right - left) / 2; mid = 1;
nums[ mid ] = 0 等于 target = 0; 成功查询到target 返回 1;
完整代码
class Solution {
public int search(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
// 循环条件
while(left <= right){
// 防止溢出, 等同于(left + right) / 2
int mid = left + (right - left) / 2;
if(nums[mid] > target) {
// target 在左区间[left mid - 1]
right = mid - 1;
} else if (nums[mid] < target) {
// target 在右区间[mid + 1, right]
left = mid + 1;
} else { // nums[mid] == target
return mid; // 在数组中找到target, 直接返回下标
}
}
return -1; // 没有找目标值
}
}
运行结果:

总结
二分查找的前提
- 数组为有序序列
- 数组中没有重复元素
- 只能查找一个元素
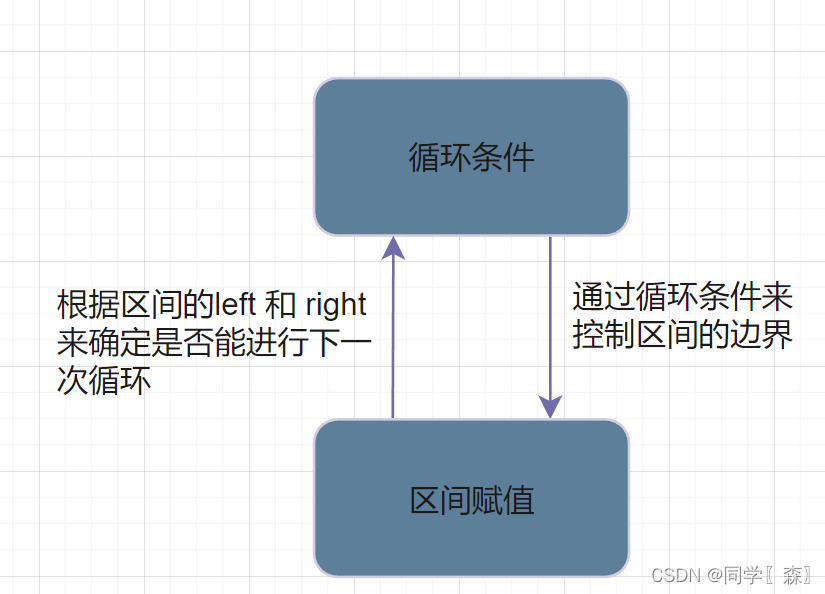
二分查找易错点
- 循环条件:
前闭后开 [left, right) 循环条件为 left < right ;
前闭后闭 [left , right] 循环条件为 left <= right;- 区间赋值问题:
left = mid + 1;
前闭后开 [left, right) right = mid ;
前闭后闭 [left , right] right = mid - 1;
本文查考信息
代码随想录
【二分查找】详细图解
作图网站
力扣
![[陇剑杯 2021]之Misc篇(NSSCTF)刷题记录④](https://img-blog.csdnimg.cn/70ede0abb56241d480e636535a33db45.png)