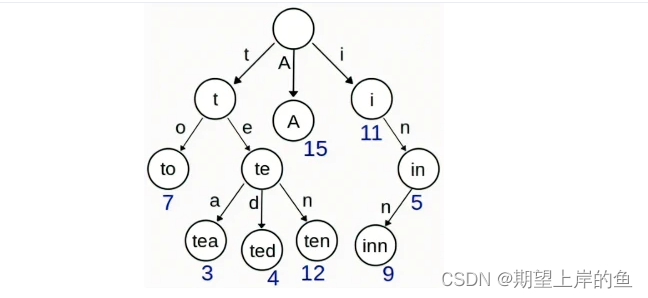
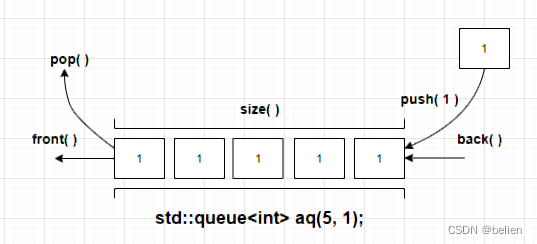
知识点回顾 ： Trie，又称前缀树或字典树，用于判断字符串是否存在或者是否具有某种字符串前缀。

❓208. 实现 Trie (前缀树)

难度：中等

Trie（发音类似 “try”）或者说 前缀树 是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。

请你实现 Trie 类：

• Trie() 初始化前缀树对象。
• void insert(String word) 向前缀树中插入字符串 word 。
• boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
• boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

实例：

输入
[“Trie”, “insert”, “search”, “search”, “startsWith”, “insert”, “search”]
[ [], [“apple”], [“apple”], [“app”], [“app”], [“app”], [“app”]]
输出
[null, null, true, false, true, null, true]

解释
Trie trie = new Trie();
trie.insert(“apple”);
trie.search(“apple”); // 返回 True
trie.search(“app”); // 返回 False
trie.startsWith(“app”); // 返回 True
trie.insert(“app”);
trie.search(“app”); // 返回 True

提示：

• 1 <= word.length, prefix.length <= 2000
• word 和 prefix 仅由小写英文字母组成
• insert、search 和 startsWith 调用次数 总计 不超过 $3\ast 10^4$ 次

💡思路：使用数组

我们要定义一个名为TrieNode的类，它有两个属性：

• childs：这是一个大小为26的数组，表示当前节点的子节点。数组的每个元素代表一个字母（从a到z）。如果当前节点有一个子节点（例如a），则childs数组的相应位置（即索引0）将包含一个TrieNode对象。
• isLeaf：这是一个布尔值，表示当前节点是否为叶子节点。如果当前节点是叶子节点，则此值为true；否则为false。

🍁代码：(Java、C++)

Java

class Trie {
    private class TrieNode{
        TrieNode[] childs = new TrieNode[26];
        boolean isLeaf;
    }

    private TrieNode root = new TrieNode();

    public Trie() {

    }
    
    public void insert(String word) {
        insert(word, root);
    }

    private void insert(String word, TrieNode root){
        if(root == null) return;
        if(word.length() == 0){
            root.isLeaf = true;
            return;
        }
        int index = indexForChar(word.charAt(0));
        if(root.childs[index] == null){
            root.childs[index] = new TrieNode();
        }
        insert(word.substring(1), root.childs[index]);
    }
    private int indexForChar(char c){
        return c - 'a';
    }
    
    public boolean search(String word) {
        return search(word, root);
    }

    private boolean search(String word, TrieNode root){
        if(root == null) return false;
        if(word.length() == 0) return root.isLeaf;
        int index = indexForChar(word.charAt(0));
        return search(word.substring(1), root.childs[index]);
    }
    
    public boolean startsWith(String prefix) {
        return startsWith(prefix, root);
    }

    private boolean startsWith(String prefix, TrieNode root){
        if(root == null) return false;
        if(prefix.length() == 0) return true;
        int index = indexForChar(prefix.charAt(0));
        return startsWith(prefix.substring(1), root.childs[index]);
    }
}

/**
 * Your Trie object will be instantiated and called as such:
 * Trie obj = new Trie();
 * obj.insert(word);
 * boolean param_2 = obj.search(word);
 * boolean param_3 = obj.startsWith(prefix);
 */

C++

class Trie {
private:
    vector<Trie*> childs;
    bool isLeaf;

    Trie* searchPrefix(string prefix) {
        Trie* node = this;
        for (char ch : prefix) {
            ch -= 'a';
            if (node->childs[ch] == nullptr) {
                return nullptr;
            }
            node = node->childs[ch];
        }
        return node;
    }

public:
    Trie() : childs(26), isLeaf(false) {}

    void insert(string word) {
        Trie* node = this;
        for (char ch : word) {
            ch -= 'a';
            if (node->childs[ch] == nullptr) {
                node->childs[ch] = new Trie();
            }
            node = node->childs[ch];
        }
        node->isLeaf= true;
    }

    bool search(string word) {
        Trie* node = this->searchPrefix(word);
        return node != nullptr && node->isLeaf;
    }

    bool startsWith(string prefix) {
        return this->searchPrefix(prefix) != nullptr;
    }
};


/**
 * Your Trie object will be instantiated and called as such:
 * Trie* obj = new Trie();
 * obj->insert(word);
 * bool param_2 = obj->search(word);
 * bool param_3 = obj->startsWith(prefix);
 */

🚀 运行结果：

🕔 复杂度分析：

• 时间复杂度：初始化为 $O(1)$，其余操作为$O(|S|)$，其中 $\mid S\mid$ 是每次插入或查询的字符串的长度。
• 空间复杂度：$O(|T|\cdot \Sigma )$，其中 $|T|$ 为所有插入字符串的长度之和，$\Sigma$ 为字符集的大小，本题 $\Sigma =26$。

题目来源：力扣。

放弃一件事很容易，每天能坚持一件事一定很酷，一起每日一题吧！
关注我 leetCode专栏，每日更新！

注： 如有不足，欢迎指正！